月相问题全解[上学期]
图片预览



文档简介
月相问题全解
广东省佛山市顺德区一中 刘华新
“月相及其变化”是高中地理上册第一单元里的内容,在2001年、2002年是必学内容,2003年开始是选学内容。2004年全国有些省份实施新课程标准,月相观测也作为一项重要的天文实践活动被选进必修教材和选修教材。对月相及其变化如何理解,是很多老师的教和学生的学都感到头痛的问题,2001年版教材课本上只提供了一幅《月相成因示意》图(图一)和一幅《观察月相》图(后面图三)另外还有一段文字说明。
以上看似内容不多,但涉及到具体的月相判断就比较复杂了,如果对月相问题没有深入的理解,要准确判断月相及其对应的日期、观测地点、月面朝向或月面和当地地平面的夹角关系就较难了。实际上要准确全面解决月相问题,需要丰富的月球天文知识和空间的想象、预判能力,对老师和学生来说这都不是一件简单的事情。为全面说明月相问题,下面我从三个方面来讲:
1、 对课本内容的理解
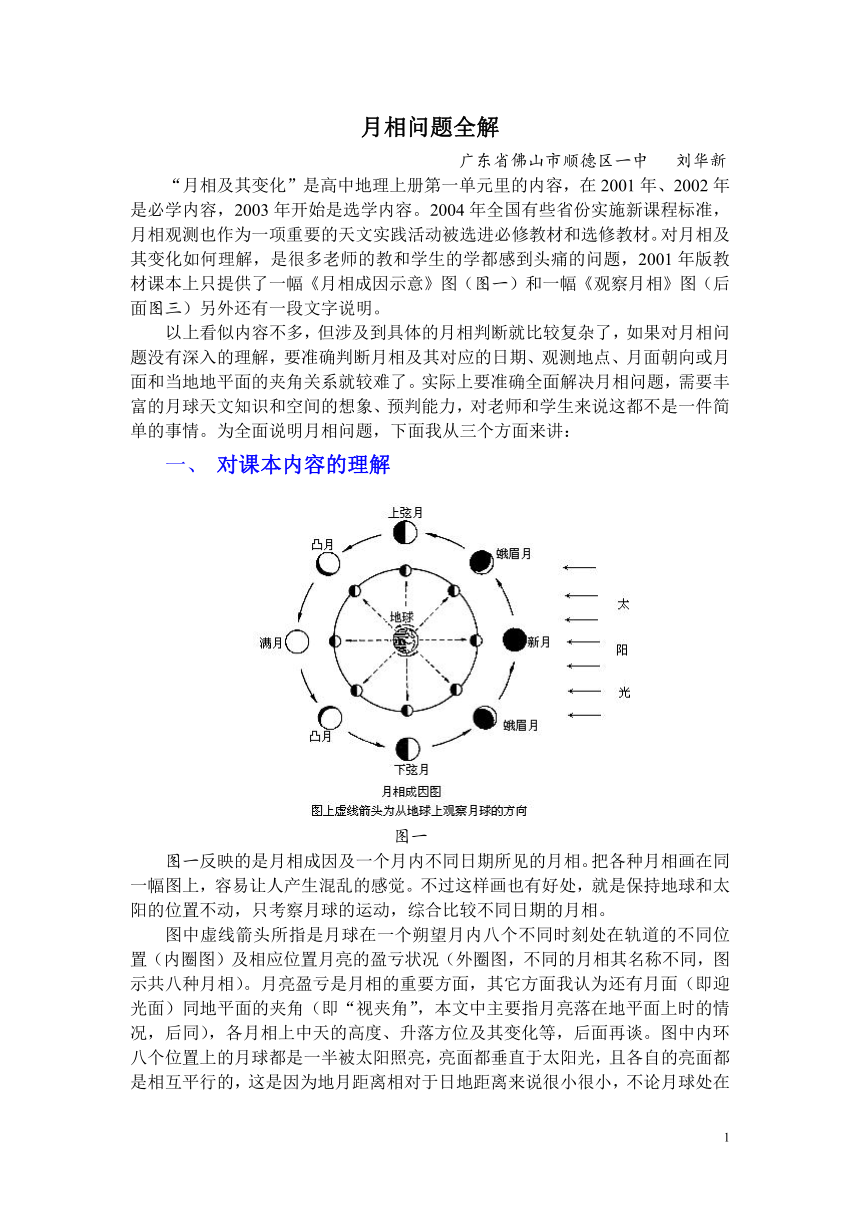
图一
图一反映的是月相成因及一个月内不同日期所见的月相。把各种月相画在同一幅图上,容易让人产生混乱的感觉。不过这样画也有好处,就是保持地球和太阳的位置不动,只考察月球的运动,综合比较不同日期的月相。
图中虚线箭头所指是月球在一个朔望月内八个不同时刻处在轨道的不同位置(内圈图)及相应位置月亮的盈亏状况(外圈图,不同的月相其名称不同,图示共八种月相)。月亮盈亏是月相的重要方面,其它方面我认为还有月面(即迎光面)同地平面的夹角(即“视夹角”,本文中主要指月亮落在地平面上时的情况,后同),各月相上中天的高度、升落方位及其变化等,后面再谈。图中内环八个位置上的月球都是一半被太阳照亮,亮面都垂直于太阳光,且各自的亮面都是相互平行的,这是因为地月距离相对于日地距离来说很小很小,不论月球处在轨道上的什么位置,我们都认为阳光是平行或极行射来的,这也是后面我们说明问题的前提和基础,是研究月相需要考虑的一个重要原理。
每时每刻,月球都是一半被太阳照亮,但为什么我们会看到月亮在一个月内有“阴晴圆缺”,即从朔到望,又从望到朔的的盈亏变化呢?这一点课本上也说的很清楚,这是因为月球在绕地球运转,日、地、月三者之间的位置关系时刻都在发生变化,地球上的人们不同时刻观测月球的角度不同,能看到的月亮的亮面的多少就不同,看上面的图也很容易理解。但从科普的角度来看,还有相当多一部分人缺乏这方面的知识,不明白月亮为什么会有圆缺的变化,他们天真地以为缺的那部分是被“天狗”吃掉了,还有更多的半懂不懂的人以为是被地球遮住了。所以科普还任重道远,在学习了这部分知识后,可消除大部分人的疑惑。
虽然课本上讲的很清楚了,但在课堂上为了讲的生动和通俗易懂,我们还可举一例:夜晚路灯照在一棵树上,我们从不同的地方看,能见到的树的光亮的部分的多少是不一样的(画草图很好解释,可画“两小儿辨树”的场景,套用和孔子有关的“两小儿辨日”的例子,这样较生动)。同理对于月球来说,它始终也只有一半是亮的。我们从不同的角度看,能见到它光亮的范围是不一样的。
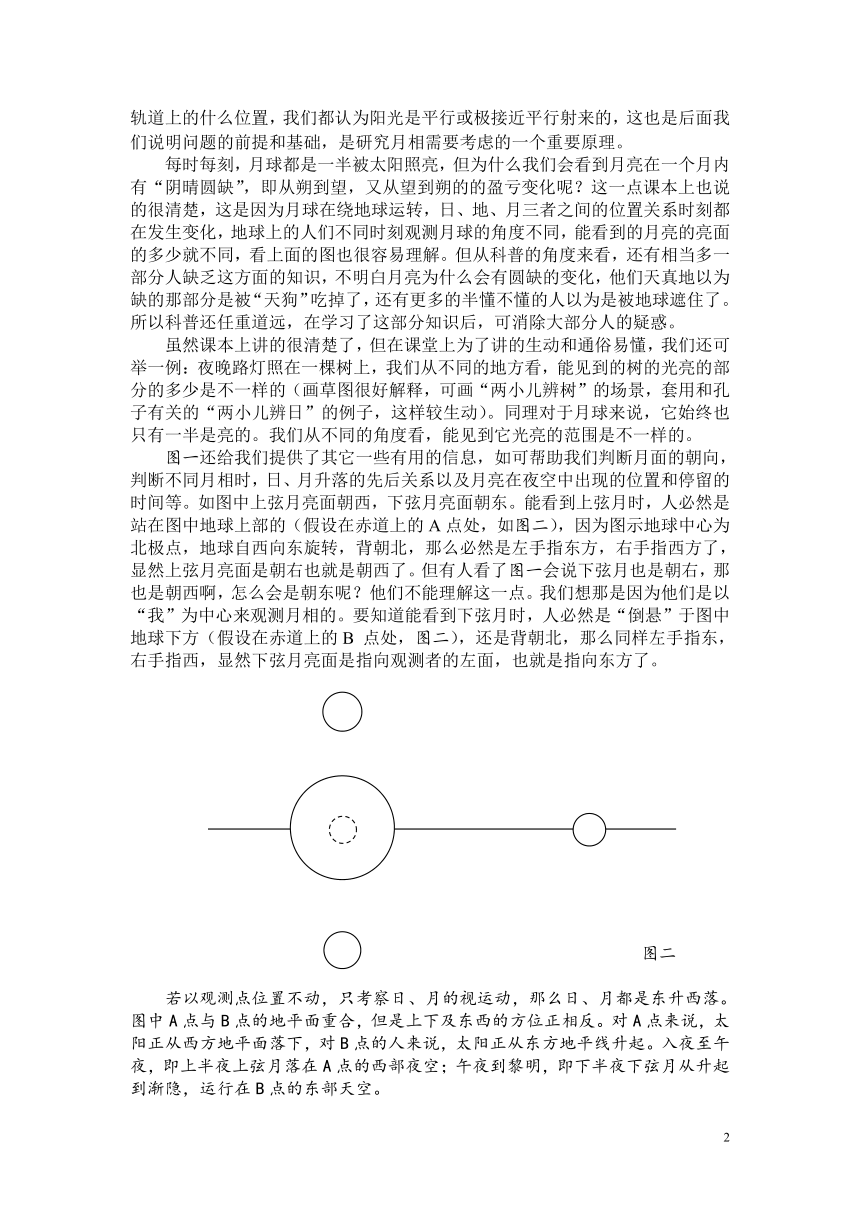
图一还给我们提供了其它一些有用的信息,如可帮助我们判断月面的朝向,判断不同月相时,日、月升落的先后关系以及月亮在夜空中出现的位置和停留的时间等。如图中上弦月亮面朝西,下弦月亮面朝东。能看到上弦月时,人必然是站在图中地球上部的(假设在赤道上的A点处,如图二),因为图示地球中心为北极点,地球自西向东旋转,背朝北,那么必然是左手指东方,右手指西方了,显然上弦月亮面是朝右也就是朝西了。但有人看了图一会说下弦月也是朝右,那也是朝西啊,怎么会是朝东呢?他们不能理解这一点。我们想那是因为他们是以“我”为中心来观测月相的。要知道能看到下弦月时,人必然是“倒悬”于图中地球下方(假设在赤道上的B 点处,图二),还是背朝北,那么同样左手指东,右手指西,显然下弦月亮面是指向观测者的左面,也就是指向东方了。
图二
若以观测点位置不动,只考察日、月的视运动,那么日、月都是东升西落。图中A点与B点的地平面重合,但是上下及东西的方位正相反。对A点来说,太阳正从西方地平面落下,对B点的人来说,太阳正从东方地平线升起。入夜至午夜,即上半夜上弦月落在A点的西部夜空;午夜到黎明,即下半夜下弦月从升起到渐隐,运行在B点的东部天空。
图一的其它六种月相,我们都可用图二所示的相同的方法来判读。所以看图一时我们应该让自己“钻”入图中,站到地球表面赤道地区附近,图中各月相,我们对它们的理解都要保证自己的观测点处于能看到它们的夜空下。能看到日、月等天体的前提是它们都得在地平面之上,能观察到月亮的前提多数情况下是太阳在地平面以下(此时段为夜),特别是对于新月和残月来讲,因为它们的亮面面积较小,即盈的少,亏的多,难以在哪怕是夕阳和朝阳的不太强的光芒中争得表现自己的一席之地。
在实际生活中人不可能倒悬空中来看书理解图一,这时可以用一个简单可行的方法:即转动书本,始终保持自己处于“站立”状态,坐北朝南,自然就是左手指东右手指西了,同时还要确定自己的地平面,再分别考察每一种月相。自己的观测点的“坐标”确定了,那么判断月面所指的方向就容易了,再考察日、月的视运动,它们升落的先后关系以及月亮在夜空中出现的位置和停留的时间就好判断了(图三下面的表有归纳)。说到底,就是你必须正确确定自己的观测点的位置,那样你的观测结果才可能是正确的。
另外要交代的是,照上述方法分析和理解图一,如图中所示都是符合客观实际的话,那么该图反映的就应该是北半球中纬度地区观测的情况。
关于下面图三,这幅图也是默认了观测者是在北半球中纬度地区。上半月和下半月图中都同时画了几个月亮,这也会让一些人迷惑不解。其实交代的是图中各种月相并不是出现在同一天,而是表示不同日期的月亮在太阳升起或落下这两个时刻在天空中的位置及相应的月相。不同的月相是不可能出现在同一天的。
图三
至于上面课本上的《月相同太阳出没的比较,夜晚见月情形》的表格,其内容完全不必死记,那样是愚蠢的,不能理解就难得记,记得一时也难长久。我们需要的是理解的记忆,前面文字已经帮助分析了,此不多说。遇到具体的问题时还要临时推导,这样才能做到准确无误。必要时可自制月相变化演示仪,或做flash动画演示,帮助对上表的理解记忆。
另外,从准确意义上来讲,此表只能反映赤道地区常年的情况或其他地区多年的平均状况,为什么这么说呢?举一例就可证明:例如二至日及其前后一段时间的极点在极夜时,如果是上弦月—满月—下弦月这样的月相,月球在地平面之上,月亮整夜可见,而遇到下弦月—朔月—上弦月的月相,月球在地平面之下,整夜不见月亮。此时处于极昼的另一个极点的情况与之正相反,从月球出没地平面的情况来看,两极点始终是此起彼落的关系,出现的月相完全不同,此时这个极点是下弦月—朔月—上弦月这样月相出现在地平面上,但是极昼时有太阳的光辉照耀,尽管月球有且必定是半个恒星月的时间在地平面之上,人们可能还是不能看初一前后的弯月,接近弦月的月相可能容易看到些。
当然上表中四种月相在中高纬地区的表现与表中所示也会有较大的出入。
还可以进一步探讨,同一时刻的月相,在地球的不同位置观测,月面的朝向也有不同,比如说蛾眉月(或新月或残月)在接近地平线时,在低纬看,月面的凸向是接近或可以朝正下方,在北极点上看,弯月是近乎竖直于地平面上的,尽管我没有到过北极,但这完全可以想象得到,这需要较强的空间想象能力。这就是我在后面面要重点讨论的问题。
这里先引入视夹角的概念,如图四,视夹角即月球迎光面同地平面的夹角,图中α 即视夹角。
2004年12月10日,农历十月 2003年11月26日,农历十一 网友拍摄之上弦月图
二十九黎明前,残月从东方升起。 月初三悬挂在约旦首都安曼一座
曾惠苹摄于井冈山,数码拍摄。 清真尖塔上方的夜空的一轮新月。
二、练习中存在的问题
市面上有关月相练习的题目,很多都有问题。一般都是给你一幅图,图中什么参照物都没有,只有月相,月相可能是弦月,可能是弯月或凸月,让你判断是上弦月还是下弦月,是初三的月亮还是二十七、八的月亮等。(图五,四种情况)
A B C D
问:A和B的半月图,哪一个是上弦月,哪一个是下弦月?
C和D,哪一个是初三的月亮,哪一个是二十八的月亮?
图中没有画出地平线也没有标出地平面上的方向,没有标出观测地点(是哪个半球,哪个纬度范围)。严格说来这样的题目是无法做的。之所以一些题目在资料上有所谓的正确的答案,我想那是他们默认了一切月相都是在北半球中纬度观测到的,且默认了弯月图的下方边框线就是地平线,对于弦月他们默认了图的左边框线是东,右边线是西,上边线为北,下边线为南;对于新月,他们不能默认图的下边框线左、右两边面是北还是南,那就只能服从于月相判断的结果了。对于新月,他们认为右面是北;对于残月,他们认为左面是北,见下面图解
(图五,四种情况) 默认是在北半球中纬度某同一地点观测
上弦月 下弦月 初三 二十八
图中的方向都是默认的,资料上没有标出来,这里我标出方向。
上弦月和下弦月都是仰望天空所见。
三、对月相判断的深入认识(创新部分)
如上所述,我们发现了练习中的问题,那么怎么样解决呢?要尊重客观实际,真正科学的题目是要以全球为考察范围的。在图中要交代地平面、地平面上的方向、月亮在地平面上的高度,观测点的位置(半球位置,纬度位置)等,甚至有必要时还要交代经度位置和观测时具体的地方时刻。知道了上面的几个条件中的其中几个,那么另外几个结果我们就可以推导出来。下面看一个具体的例子:
有一次我在看中央电视台的节目《两极之旅》时无意中发现了一个镜头,即日出前的弯月,当时是摄制组的人员到安第斯山顶去拍摄温泉在日出前的那种云雾蒸腾的样子,以显示温泉热度之高和景象之壮观,当镜头指向黎明前的泛白的东方时,我发现一轮弯月在东方地平线上,弯月的凸面是向右下方凸出的(图六、下右图)。
落基山脉观测 安第斯山脉观测
(图七) (图六)
这使我要思考其道理,很快我明白了其中的道理,我进一步想,假如此时在北美洲的落基山脉看这轮弯月,又是什么样的景象呢?不难理解,在地平线上月面应该凸向左下方(图七,上左图)。我一直在思索和判断在地球的不同的地方观看月亮,月相形状同地平面的相对位置关系是不同的,以前我在课堂上也给学生们讲过这一点,我举的是赤道和北极点对比这个例子,这两点的人站立的角度相差90°,那么他们观测到的位于赤道地方的地平面上东方或西方遥远的接近地平面的物体的视角自然相差90°(见下面原理图,图八)。在图中我们是可以推断出其几何原理的,在电视上看到的镜头进一步证明了我以前的推理,这里可帮助理解上面图六和图七的不同。
赤道所见 北极所见
(图八)
根据同样的原理,我们还可以想象和推断出在地球各地,不同的时刻观测到的各种月相的情况。
但是,在判断前我们要知道如下几点前提条件:
1、 球绕太阳运动的轨道叫黄道,月球绕地球运动的轨道叫白道,白道和黄
道是有一定的交角的,但交角不大(为5°09′),从每个月来看月球有一半的时间在黄道面以下,一半的时间在黄道面以上(准确地说是半个交点月的时间,一个交点月是27.21222日),这样从全月、全年的平均状况来看可以认为月球的位置就在黄道面上,我们可取这个平均值来看问题。
2、同一天,地球各地见到的月相的形状,即盈亏状况是一样的。其原理是对于遥远地方的天体来说,可以认为地球就是一个点。
3、月球的视半径是15分33秒,接近太阳的视半径。
4、当然我们最好还要了解月球距离地球平均为38.4万千米,一个朔望月的周期是29.5306日,一个恒星月周期是27.32日,自转周期也是27.32日,恰好和恒星月周期相同,这决定了月球始终只有一面对向我们地球,即所谓的“正面”,而它的背面我们在地球上是永远也看不到的。
遇到具体问题时具体分析,都可以得到特定的结果,为了叙述上的方便,我们就以上面的4点所说的平均状况来分析问题。为了使问题的说明更具有条理性,我们按春分、秋分、夏至、冬至四个节气分别来谈不同纬度地点所见不同月相的情况,选南、北极,南、北纬45°,赤道,共5个地点来观测,重点选新月(具体到初二或初三),残月(具体到阴历二十八或二十九)。
这样看来,4个时间,5个地点,2种月相,组合起来工有40种不同的观测结果(见图九,组图)。上、下弦月,凸月及满月另外再简单地谈谈。
1, 春分时各地观测月相情况:(准确地说应该是月球位于春分点的情况,余类推)
1, 新月(阴历初二或初三)
南极点 南纬45° 赤道 北纬45° 北极点
(各幅图下边的框线为地平线,除南、北极点外,其
正中的方向为正西方或正东方,下面各组图道理相同)
2, 残月(阴历二十八或二十九)
北极点 北纬45° 赤道 南纬45° 南极点
(凡是新月日,落后出现在西方地平线;凡是残月,日出前出现在东方地平线)
二,秋分时各地观测月相情况:
1, 新月
南极点 南纬45° 赤道 北纬45° 北极点
2,残月
北极点 北纬45° 赤道 南纬45° 南极点
(残月和新月与太阳升落时间都很接近,春、秋分时升落方位是正东正西)
3, 夏至时各地观测月相的情况
1, 新月
南极点 南纬45° 赤道 北纬45° 北极点
(南极点处于极夜,无法见到新月,北极点处于极昼,月球高度接近23°26′,月弓和地平面的夹角为90°。但是极昼时,太阳和新月同在地平面上,能否看到新月,还要视乎当时的情况,前面已有论述,也许初三以后的月亮容易看到些,有待考察。下面几幅极点的图的情况用相同的方法分析)
2, 残月
北极点 北纬45° 赤道 南纬45° 南极点
4, 冬至时各地观测月相的情况
1, 新月
南极点 南纬45° 赤道 北纬45° 北极点
2,残月
北极点 北纬45° 赤道 南纬45° 南极点
(图九,组图)
(注:为了叙述方便和讲清原理,以上都不计较日月细微的黄经差。另外在实际观测中,新月、残月的“月尖”部分由于视直径太小而难以被肉眼看到,不能如图中所画理想状况那样月弓可以达到一个半圆弧)
从夏至和冬至各组图还可看出:夏至时,各地的新月都从西偏北落下,残月都从东偏北升起,基本等同于太阳的升落方向,其天文原因是新月、残月和太阳的黄经、赤纬相差不大。同样的原因,冬至时,各地的新月都从西南落下,残月在东南升起。
以上各图都标明了“月弓”在接近地平面时和地平面的夹角,其理论依据在于要知道当时日、地、月的位置关系,日、月在黄道上的位置。这里我们还要知道月弓的竖直方向与黄道面是垂直的,月球迎光面与地球晨昏圈平面是平行的,这可画立体视图说明。这样,各种情况我们都可画相应的便于观察和分析的视图,从而推算出“月弓”同地平面的夹角。上图中冬、夏至时南、北纬45°地方的夹角50°41′,这要利用球面三角知识求出来,这里就省略画图和公式的推导与计算了。如能用三维动画来演示,效果更好。
通过深入研究,我们发现利用天球仪器来演示不同月相在不同时间的位置,视夹角则更直观。后述各种情况一样,若用天球仪演示更直观。
对于弦月、凸月来讲,我们可以根据上述的原理,用同样的方法推算出它们的视夹角,但是它们的形状看起来更接近“块状”,而不象新月、残月那样接近“条状”,也因为它们不象新月、残月那样只是在日落、日出前后不久出现在地平线上不高的位置,所以研究它们同地平面的夹角“意思”不大或观察时间不方便,更因为考虑到叙述上的不方便,这里只对它们的月相状况作简略讲述。取全球各地的平均位置即赤道在多年的平均月相状况来看(见图十,组图)。又有以下几种情况:
1,上半夜西部夜空上弦月的情况 2,下半夜东部天空下弦月的情况
日落时仰望星空 午夜时西方地平线 午夜时东方地平线 日出前仰望星空
3,十五前的凸月在地平面上的情况 4,十五后的凸月在地平面附近的情况
日落后东方地平线 日出前西方地平线 日落后东方地平线 日出前西方地平线
(上面四个图中“日出前”、“日落后”分别都取极相同的地方时刻,可以看出在相同的地方时刻,十五前后的月亮在地平面上的高度不同。图中所示日出前的地方时刻以十五前的凸月靠近西方地平线为准,日落后以十五后的凸月升上地平面为准,这样才有了上图不同月相的相同地方时刻在地平线上的高度对比)
5,凸月在上中天时的情况
(十五前的凸月,午夜前一点仰望星空, (十五后的凸月,午夜后一点仰望星空,
月面朝西,接近上弦月的情况 ) 月面朝东,接近下弦月的情况)
(可以说十五和初一是月面朝向的一个分水岭)
(图十,组图)
十五的月亮(满月),我们研究所能见到的它的亮面和地平面的夹角关系没有多大的意义。但是我们可研究它升起和落下的方向和时间,以及它到达中天的高度。可以概括地说各地满月的升落方向、升落时间、当夜最大月亮高度角与当日的太阳在上述几个方面的表现密切相关,情况应该是正好相反。比如,北半球夏半年太阳从东北方升起、升起时间必然在6时以前,北半球地区正午太阳高度角就大,傍晚在西北方落下,落下时间在下午六时以后。那么当地当日的月亮是从东南方向升起、升起时间是在下午六时以后,北半球月亮到达上中天时高度角小,在西南方向落下,落下时间是在六时以前。为什么会这样呢?从天文意义上理解其原因,是因为十五的时候太阳的黄经和月球的黄经相差180°,赤纬数值相同,但方向正好相反,一个在北赤纬,那么另一个必然在南赤纬。也可通俗地理解其带来的结果:十五的月亮和太阳的关系是“此升彼落”即“你东我西”的关系,当然还有“你北我南”、“你早我迟”和“你高我低”的相反或对称关系。
其他的情况可类推。
所以要详尽研究月球与太阳的升落时间关系、月球的上中天高度,那还要看当日它们之间的黄经差,各自的赤纬数等。
理解了上述原理我们还可以回答这样的问题:俗语说“月到中秋分外明”,那么中秋的月亮是一年中最明亮的吗?
通过长期的观察和分析,我们认为“月到中秋分外明”这只是诗人,文学家的语言。实际上中秋的月亮不是一年中最明亮的,为什么呢?要回答这个问题还是先从对我们本月的观测结果分析开始。我们还记得今年(2005年)9月13号夜晚8点半左右我们看到的上弦月的上中天高度只有45°左右,而到了二十二、三,黎明时月亮高度可近90°,这样看来月球在不同的时候能达到的上中天高度也是不一样的。(观测地点:顺德一中,北纬22°50′)
我们可画图分析:选秋分日恰好为上弦月的特殊情况,如下图:(图十一)
白道(此图中为月球真运动轨迹)
月球一个月在白道上走一圈
黄道(太阳视运动轨迹)
太阳一年在黄道上走一圈
此图反映的是本月月相为上弦月时的日、月相对位置。从图中可看出,九月份的太阳落在秋分点附近,月相为上弦月时,月球必然落在图中所处A点的位置,对应于黄道上冬至点的位置。这里须交代一下,月球绕地公转的轨道叫白道,白道面与黄道面不在同一个平面上,但它们之间只有一个很小的夹角为5°09′,为了研究月相的方便,此处我们可以近似地认为白道与黄道在一个平面上(准确的计算月球赤纬则还要考虑黄赤交角和黄白交角的叠加,月球赤纬最大可达28°多),所以此图中上弦月的位置对应于黄道上的冬至点,月光直射点在南回归线附近,这样我们在北半球看月球上中天的高度就很低了。本月的下弦月时,月球落在图中B点附近的位置,对应于夏至点,月光直射在北回归线附近,月球上中天的高度自然就高了。观测结果确实是这样。
一年中什么时候月亮最明亮呢?除了月要圆之外,还要月亮的上中天高度最大,要满足上中天高度最大,月球必须在夏至点附近,对于北半球而言,此时月球赤纬最大,而此时要满足月最圆的条件须是农历十五,这时候只有太阳落在冬至点附近才行,即是冬季的十五月亮最明亮。这样看来“月到中秋分外明”就不能说是全年中最明亮的了。
又比如说2003年全国天文奥林匹克竞赛低年组卷里有这样一道题目:
月亮绕地球公转的轨道平面和黄道只有一个非常小的夹角。请问,上弦月发生在一年的什么时候(比如几月份左右),在上中天时可以有最大的地平高度?(假设你在北京观测)。
用同样的方法可推断出:上弦月上中天的地平高度极大值的时期是春分时的上弦月,但是不可能每次春分时恰好为上弦月,所以答案应该是三月份左右的上弦月。
由此还可推导:对于北半球回归线以北地区来说,秋分时上弦月地平高度最小,下弦月的情况与此正相反。还可推导夏至时满月的中天高度达到最小。
以上是定性的分析,也需要较强的空间思维能力。如有了一定的天文、数学基础知识的话,我们还可用相关的公式来计算,这要用到球面三角理论。
不论是求月面与地平面的视夹角,还是求各月相的上中天高度,前面我们举的春、秋二分,冬、夏二至都是特殊的情况,各节气又刚好对应新月、残月,或上、下弦月就更特殊了。事实上不可能每次情况都和上述的相对应,即在上述节气不可能每次都是初二、三,或初七、八,十五,二十八、九等,这时候就要求考虑非特殊的情况了。比如说2004年3月20日是春分,当日是农历三十,这样节气与新月的出现是很对应的,可以套用前面的组图八来分析。而2004年4月22日农历初四不属于二分二至节气,当日夜晚天气好,我用双筒望远镜观测了西部天空,看到金星之下是一轮明亮纤细的弯月,在它将接近地平面时与地平面只有很小的夹角,看起来几乎是平行于地平面。具体夹角是多少呢?这需要用公式计算,因为前面我也说过月球的亮面和黄道面始终是垂直的,所以我们只要求出当日月球到达地平面时,黄道面与地平面的二面角就行了。
我所在的广东佛山市顺德区一中纬度是北纬22°50′,地平面与赤道面的交角为67.17°。当日太阳的黄经是在春分点以东约(33日/365.2422日)*360°=32.526°,初四月亮接近地平面时为晚上8时30分左右,所以月球与太阳的黄经差为 (3.85日/朔望月29.53日)*360°=46.935°(这里默认了初一零点时月球与太阳黄经相同,具体数据查天文年历更准,这里重点突出计算方法),落在太阳以东,所以月球的黄经为上述两式数值之和,约为79.46°,比较接近夏至点。当月球刚好落在西部地平面上时,黄道、赤道、地平圈共同组成了一个相应的球面三角形,在这个三角形中可求出黄道面和地平面的交角。经过一系列复杂的计算,得知交角为69.63°,黄道面向南倾,所以月面与地平面的夹角就是69.63°的余角 ,为20.37°,向北倾(见图十一),可以看出这个倾角是很小的。同一日,北京地方的弯月与地平面的夹角也可计算出来约为49°,倾角明显大于低纬所见。
广东佛山市顺德一中所见 北京地区所见
图十二
用此方法还可求出任意日期里月面与地平面的视夹角。可以概括性地说,也是一个重要的原理:月球落在地平面上时,月面(即所见迎光面部分,或弯月或凸月)与地平面的视夹角都等于当时当地黄道面与地平面夹角的余角或补角。地平面与黄道面的夹角随着地球的自转又在不断地变化,也许我们可以推导出此夹角在一日内随时间变化的函数表达式。在特定黄道位置上的月亮在某日内一定会在特定的时间落在地平面上,利用函数式我们可以即时求出月面与地平面的视夹角。月球在其它地平高度时,视夹角则需要更为复杂的计算才能求出,进一步推导,我们也可得出相应的公式,只要有了一定的参数,其它地平高度的视夹角都是可求出来的。如何计算,另可见我写的文章《在天文观测中推求球面三角关系》,此不细述,容后分析解答。
月相判断看似复杂,但也有规律可循,还可以补充和归纳以下几点:
①月相盈亏的多少决定于它距初一或十五的远近,或是它与太阳黄经差的大小。月相盈亏的多少也决定了月亮在夜空中停留时间的长短,成正相关。
②弯月和凸月的外圆弧长都始终等于180°。从几何意义上看,这还可以帮助我们画出正确的月相。“外圈”为半圆弧,“另一半”是长轴等于月球直径的半个椭圆弧。(如图十三)
③月亮盈亏多少相同的情况下,到底是十五前,还是十五后的月亮,则要看当时月面的朝向了。是在哪个半球,哪个纬度观测的则要看相应时刻月面与地平面的视夹角及月面的倾向了,如前述各组图。
④从多年平均状态来看,各种月相落入地平面时其视夹角北半球向北倾斜,南半球向南倾。不论南、北半球,纬度越高,倾角越大。无论哪种月相,其“视夹角”多年平均等于当地的纬度值。赤道地区多年平均无倾角。
又深入分析和论证第④点,多年平均,各种月相落入地平面时,视夹角应该等于当地的纬度值。就拿赤道地区的上弦月这种特殊情况来看吧(如图十四)
夏至 春分 秋分 冬至
图十四
绘此图的基础是要知道上弦月与太阳黄经相差90°且落在太阳以东,
另外要保证日、地、月都在黄道面上,保证黄赤交角为23°26′。)
此时赤道上的A点是午夜,月亮正落入到西方地平面,夏至时其与地平面的夹角为北倾23°26′,方位正西;春分时夹角0°,方位西偏北;秋分时夹角0°,方位西偏南;冬至时夹角南倾23°26′,方位正西。这样从全年平均来看,上弦月是从正西落下的,弦月面与地平面夹角平均为0°,即等于赤道的纬度0°。
另外拿北纬45°地区的新月来看,参看前面组图九,从春分—夏至—秋分,夹角是由最小到最大,即由21°34′到68°26′,平均起来等于45°,即当地的地理纬度。从秋分—冬至—春分,又从最大到最小。巧的是冬、夏二至时夹角相同,都为50°41′,但是落下的方位不同,夏至在东北方落下,冬至在西南方落下。
以上也只能算是定性加简单定量分析和论证,因为也只是取了特殊的情况。
还可以进一步定性分析论证:某月相每月出现一次,各月该种月相在黄道上的位置不同,但是多年来看,它可均匀地分布在黄道上的任何位置。而地平面同黄道面的夹角每天(严格来说是一个恒星日)变化一个周期,从全天夹角的平均值来看,等于当地纬度的余角值,这有待建立数学表达式。这里不考察每天的情况,考察的是上述月相每月一次落在地平面时的“黄地”夹角,其各月也在变化,但多年平均也应该等于当地纬度的余角值,即全天的平均值。月面与黄道面始终是垂直的,所以月面与地平面的平均视夹角多年平均就等于“黄地”夹角的余角值,即当地的纬度值了。目前的分析和论述只能到此,关于其它地平高度的平均情况更不是一时半会儿说得清楚的,如前面文字所述,有必要时要建立一个数学模型,考察其视夹角的时刻变化。
用数学方法来证明上述第④点结论,还需要较大的篇幅,我想公式的推导和结果也应该是十分美妙的。
月相判断,如只想粗略了解,难度并不大,但要深入研究,则难度并不小。通过深入研究,能丰富我们的天文知识,增强空间想象能力,其教育内涵是极其丰富的。
本文第一部分主要从学习的角度来讲,本想更简洁一些,但还是略显罗嗦,但这部分是基础,是对解决后面问题的铺垫。其实有很多人写过关于这部分内容的文章,方法多种多样,各有千秋,不可拘泥于一种形式。文章第二、三部分则是对月相及相关问题的深入分析,是本文的重点。
本文力求用通俗的语言讲清一些浅显的道理,同时又不回避难点问题,敢于深入挖掘和拓展研究,重点研究了月面与地平面的夹角和观测地点、观测时间的对应关系,主要月相上中天的高度和月份、日期,观测地点的对应关系等。很多问题先从定性的角度去讲并用实例予以佐证,最后上升到定量分析的高度,这也是我要追求的效果。深入研究,则不可避免地要用到了数学中的球面三角知识,有些特殊情况可直接导出结论,如组图九,主要靠的是空间想象力和简单的计算,就没有用繁琐的数学公式表达了。但是在考察非特殊情况的时候就要用到复杂的数学计算了,这需要较强的数学能力。
研究月相问题或是其它天文问题,需要较强的空间思维能力,本文用了较多的图解,能否从正确的角度去看图也是理解本文的关键所以在。
本文力求全面解答月相有关问题,但是要说明各种具体的情况,短短的篇幅是做不到的,在实际研究中还要详细取得各种参数,才能得到精确的结果。
刘华新
2003年九月初稿
美月欣赏:
趣味分析:
上图能清楚地看到弯月和地平面的夹角关系。根据前述理论,如果是在北半球拍摄的,月弓向右倾,那应该是新月。反之,知道了是新月,那应该是在北半球拍摄的,这有必然的对应关系。如果是在南半球拍摄的,那应该是残月。残月必然要在凌晨拍摄,但又有谁会在黎明前出来小坐并溜狗赏月呢?所以这幅照片多数可能是在日落后北半球某地拍摄的。
进一步看,地平线上枯枝落叶或嫩芽初发的植被景观,显示着这更可能是在较高纬度的秋冬或冬春季节拍摄的。弯月呈白色,而不是呈红色,这说明近地平面上水汽较少,这在较高纬度更加明显,这可能也是一个证明。既然是在较高纬度,根据前面的推算,如果是秋季,新月位于秋分点附近,那时的视夹角是最大的,可达到60°以上,但是目测照片中月亮的视夹角却不大,不到45°,根据前述分析,月球位于春分点时才有这种可能。当新月位于春分点附近,太阳也应在春分点附近,季节为春天。所以这幅图很可能是在冬末或春初拍摄的。
再看这植被类型,怎么看都不像是欧洲的,所以可能是在欧洲以外的季风气候区气候区拍摄的。
如果知道了拍摄的具体日期,我们可以推知拍摄地纬度。反之,如果知道了具体的拍摄地点,我们也可以推出拍摄的日期。
照片中月弓同地平面的大致夹角是可目测出来的。
新月抱旧月:
上图所展示的是一种俗称为“新月抱旧月”的现象,一弯新月怀抱中隐约可见的暗灰色光实际是地球反射的太阳光照到月面上又反射回来的光。上图是天体摄影家laurent laveder从pic du midi天文台拍摄到的
这幅图是在Pic du Midi天文观测台拍摄的
The Pic du Midi Observatory is located at an altitude of 2890 meters (9470 feet) on an isolated summit of the Pyrénées range which separates France from Spain.
( Pic du Midi天文观测台是位于将法国和西班牙分开的比利牛斯山脉的一座海拔2890米,即9470英尺的孤立的山峰上。)
从地图上看比利牛斯山脉的位置,该天文台纬度大致是北纬43度左右,北半球弯月月面向右倾斜必然是新月。从月面的盈亏来看像是初四、五左右的月亮,图中看不到地平面,如果摄影家是朝水平方向拍摄的,可以看出月面同地平面的夹角较大,大概能达到67度。根据前述原理分析,这张照片应该是秋分前后拍摄的。
这幅图及资料介绍来源于网址:
http://webast.ast.obs-mip.fr/patrimoine/asp.html
附:原理图:
1. 春分
新月 残月
2. 秋分
新月 残月
3. 夏至
新月 残月
4. 冬至
新月 残月
以上各图始终都保持黄道面和赤道面的交角为23度26分
5.月球迎光面和黄道面的关系:月球迎光面始终垂直与黄道面
6. 2004年4月22日,月球落在北纬22°50′ 的西部地平面上A时,黄道面、赤道面和地平面组成的球面三角图:ABC组成球面三角形,B是春分点,C是地平圈与天赤道的交点(西点)。
设AB弧为c,c=79°28′,设AC弧为b、BC弧为a,
已知∠B = 23°26′ 、 ∠C = 67°10′ 求出∠A 。
先根据正弦公式 可求出sinb = 0.42 、 cosb = 0.90752
又根据余弦公式
代入已知数到上两式所组成的二元一次方程组,可得:
求出sina≈1
再将它代入正弦公式(或)中
sinA =
A = = 69°38′或110°22′
角A实为钝角,即等于110°22′
但在地平面以上黄道面则向南倾,倾角则为110°22′的补角 69°38′
月弓(即月球迎光面)在地平面上的倾角为90°- 69°38′ = 20°22′
文章后记:
本文于2003年九月就完成初稿,形成了基本的思想,2004年6月在广东省天文学术讨论会上宣读,获得好评。但是文章并没有在一些杂志上发表,自己也没有刻意追求这一点,主要是考虑到文章还有很多表述上的不成熟,自己又没有足够的时间来做这一工作,所以就拖了很长时间。随着时间的推移,文章的时效性就在变化,同时我新的想法也不断涌现,所以每隔一段时间又觉得有必要修改,使文章的时效性更强和表述上更合理,更简洁一些。
在最开始写文章时,我并没有接触到相关的天文软件,后来接触到了一些好的天文软件,我在文章所写的,天文软件都能很好地演示,而且能证实我所写的都是正确的。这样看来我好象是做了一件“多余”的罗嗦的工作,天球仪我早有接触,也有一个,用天球仪也能很好地说明我所写的一些道理。看似多余,但是我觉得有必要,有收获。要说有什么收获,那就是看起来很直接的结果,我从理论上加以了推导和证明。打个比方,知道了直角三角形的两个直角边,那斜边等于多少呢?最直接,最“粗鲁”的方法就是拿一个直杆套上去当斜边,然后把直杆取下来,用尺一测量,就知道斜边等于多少。方法虽然粗鲁,但是效果却是最好的。那至此就不研究了吗?斜边更长的时候,你找不到那么长的直杆怎么办呢?所以必须找到计算的方法,上升到理论高度。我这里想说的就是天文软件或天球仪器虽然方便,但不能代替一切。再说只有弄懂了基本原理,你才能更好地理解和使用软件。当然使用天文软件和天球仪也让我明白了一个道理,那就是凡事能简洁就尽量简洁,哪怕是复杂的理论推导,因为繁琐不是科学,科学应该尽量简洁明了,而只有对一个问题理解最深刻全面时,才能达到简洁的境界。
写这篇文章让我收获不小,要深入研究月相就必然要涉及到天球坐标,还有球面三角知识,为此我专门研究了球面三角,并于2004年4月完成了《在天文观测中推求球面三角关系》,用比较独特的方法证明了球面三角的正弦、余弦定理。参加我的“月相问题研究性学习”小组的学生也有不小的收获,他们完全理解了相关问题,在天文观测和数学上学到了很多的东西,可以说完成了这一课题,他们的天文观测已基本入门了。学生有收获,老师也感到欣慰。
文章倾注了我大量的心血,这倒不是说基本问题的思考和主要思想的形成费神,而是在语言的反复推敲,版面的控制以及绘图上花了我太多的时间,这里要特别说一下绘图的问题,文中本应还有一些通俗的,生动的图的,但是我不会画。就算文中已画的图也没有画好,电子版的图我无法画好,如“原理图”中的地球要画出昼夜半球才便于让人理解,等等。文章需要给人看时我就打印文章,再手工填绘好图,复印给人看。
写这篇文章事实上我扮演了几角色:一是地理教师,要想法让学生更容易地理解课本上的基本知识;二是研究者,力求有所创新,有所发现;三是科学普及者。要说真有什么大的发现,实不敢当,所以我更愿意认为我是在做一点科学普及工作,普及一些最基本的天文知识。我现在不好把这篇文章归为哪一类,这也是一些专业取向很强的杂志不好发表我这篇文章的原因。现在文章只好这样了,基本保持其本质和原貌,那读者就各取所需要吧,现我把文章发给有关的杂志、网站和专家、个人,望共同探讨,并希望各位专家、学者、个人多提意见。
2006年8月
北南
东南
北倾50°41′
竖直90°
南倾50°41′
水平0°
南拿
北南
西南
北倾50°41′
南倾50°41′
水平0°
竖直90°
北
南
东南
水平0°
南倾50°41′
北倾50°41′
竖直90°
北南
南南
西南
南倾50°41′
竖直90°
北倾50°41′
北南
南南
东南
北倾21°34′
左倾66°34′
南倾23°26′
南倾68°26′
倒转左倾66°34′
北南
西南
南南
左倾66°34′
北倾23°26′
北倾68°26′
倒转左倾66°34′
南倾21°34′
南南
北
东
南倾21°34′
右倾66°34′
北倾23°26′
北倾68°26′
倒转右倾66°34′
西南
北
南
右倾66°34′
北倾21°34′
倒转右倾66°34′
南倾23°26′
南倾68°26′
北极
南极
正前为东方
北
南
赤道
南
南
南
北
南
北
东
西
北
北
黄道面
A
A
A
东
西
O
C
B
A
赤道地区,
新月水平落下
方位西南
赤道地区,
残月水平升起
方位东南
赤道地区,
残月水平升起
方位东北
赤道地区,
新月水平落下
方位西北
南回归线地区,新月水平落下
北回归线地区,残月水平升起
虚线和箭头表示黄道及地球公转运动方向,阴影部分为夜半球,下同
只有北回归线地区,新月水平落下
只有南回 归线地区,残月水平升起
水平0°
北拿
东拿
西拿
南拿
北拿
东拿
西拿
南拿
东拿
西拿
北拿
北拿
西拿
东拿
西拿
东拿
南拿
南拿
西拿
西
南拿
北
南拿
北
北倾20.37 °,位置西偏北
北倾49 °,落下晚
北京所见月亮倾角更大,落下时位置更靠西北。
PAGE
14
广东省佛山市顺德区一中 刘华新
“月相及其变化”是高中地理上册第一单元里的内容,在2001年、2002年是必学内容,2003年开始是选学内容。2004年全国有些省份实施新课程标准,月相观测也作为一项重要的天文实践活动被选进必修教材和选修教材。对月相及其变化如何理解,是很多老师的教和学生的学都感到头痛的问题,2001年版教材课本上只提供了一幅《月相成因示意》图(图一)和一幅《观察月相》图(后面图三)另外还有一段文字说明。
以上看似内容不多,但涉及到具体的月相判断就比较复杂了,如果对月相问题没有深入的理解,要准确判断月相及其对应的日期、观测地点、月面朝向或月面和当地地平面的夹角关系就较难了。实际上要准确全面解决月相问题,需要丰富的月球天文知识和空间的想象、预判能力,对老师和学生来说这都不是一件简单的事情。为全面说明月相问题,下面我从三个方面来讲:
1、 对课本内容的理解
图一
图一反映的是月相成因及一个月内不同日期所见的月相。把各种月相画在同一幅图上,容易让人产生混乱的感觉。不过这样画也有好处,就是保持地球和太阳的位置不动,只考察月球的运动,综合比较不同日期的月相。
图中虚线箭头所指是月球在一个朔望月内八个不同时刻处在轨道的不同位置(内圈图)及相应位置月亮的盈亏状况(外圈图,不同的月相其名称不同,图示共八种月相)。月亮盈亏是月相的重要方面,其它方面我认为还有月面(即迎光面)同地平面的夹角(即“视夹角”,本文中主要指月亮落在地平面上时的情况,后同),各月相上中天的高度、升落方位及其变化等,后面再谈。图中内环八个位置上的月球都是一半被太阳照亮,亮面都垂直于太阳光,且各自的亮面都是相互平行的,这是因为地月距离相对于日地距离来说很小很小,不论月球处在轨道上的什么位置,我们都认为阳光是平行或极行射来的,这也是后面我们说明问题的前提和基础,是研究月相需要考虑的一个重要原理。
每时每刻,月球都是一半被太阳照亮,但为什么我们会看到月亮在一个月内有“阴晴圆缺”,即从朔到望,又从望到朔的的盈亏变化呢?这一点课本上也说的很清楚,这是因为月球在绕地球运转,日、地、月三者之间的位置关系时刻都在发生变化,地球上的人们不同时刻观测月球的角度不同,能看到的月亮的亮面的多少就不同,看上面的图也很容易理解。但从科普的角度来看,还有相当多一部分人缺乏这方面的知识,不明白月亮为什么会有圆缺的变化,他们天真地以为缺的那部分是被“天狗”吃掉了,还有更多的半懂不懂的人以为是被地球遮住了。所以科普还任重道远,在学习了这部分知识后,可消除大部分人的疑惑。
虽然课本上讲的很清楚了,但在课堂上为了讲的生动和通俗易懂,我们还可举一例:夜晚路灯照在一棵树上,我们从不同的地方看,能见到的树的光亮的部分的多少是不一样的(画草图很好解释,可画“两小儿辨树”的场景,套用和孔子有关的“两小儿辨日”的例子,这样较生动)。同理对于月球来说,它始终也只有一半是亮的。我们从不同的角度看,能见到它光亮的范围是不一样的。
图一还给我们提供了其它一些有用的信息,如可帮助我们判断月面的朝向,判断不同月相时,日、月升落的先后关系以及月亮在夜空中出现的位置和停留的时间等。如图中上弦月亮面朝西,下弦月亮面朝东。能看到上弦月时,人必然是站在图中地球上部的(假设在赤道上的A点处,如图二),因为图示地球中心为北极点,地球自西向东旋转,背朝北,那么必然是左手指东方,右手指西方了,显然上弦月亮面是朝右也就是朝西了。但有人看了图一会说下弦月也是朝右,那也是朝西啊,怎么会是朝东呢?他们不能理解这一点。我们想那是因为他们是以“我”为中心来观测月相的。要知道能看到下弦月时,人必然是“倒悬”于图中地球下方(假设在赤道上的B 点处,图二),还是背朝北,那么同样左手指东,右手指西,显然下弦月亮面是指向观测者的左面,也就是指向东方了。
图二
若以观测点位置不动,只考察日、月的视运动,那么日、月都是东升西落。图中A点与B点的地平面重合,但是上下及东西的方位正相反。对A点来说,太阳正从西方地平面落下,对B点的人来说,太阳正从东方地平线升起。入夜至午夜,即上半夜上弦月落在A点的西部夜空;午夜到黎明,即下半夜下弦月从升起到渐隐,运行在B点的东部天空。
图一的其它六种月相,我们都可用图二所示的相同的方法来判读。所以看图一时我们应该让自己“钻”入图中,站到地球表面赤道地区附近,图中各月相,我们对它们的理解都要保证自己的观测点处于能看到它们的夜空下。能看到日、月等天体的前提是它们都得在地平面之上,能观察到月亮的前提多数情况下是太阳在地平面以下(此时段为夜),特别是对于新月和残月来讲,因为它们的亮面面积较小,即盈的少,亏的多,难以在哪怕是夕阳和朝阳的不太强的光芒中争得表现自己的一席之地。
在实际生活中人不可能倒悬空中来看书理解图一,这时可以用一个简单可行的方法:即转动书本,始终保持自己处于“站立”状态,坐北朝南,自然就是左手指东右手指西了,同时还要确定自己的地平面,再分别考察每一种月相。自己的观测点的“坐标”确定了,那么判断月面所指的方向就容易了,再考察日、月的视运动,它们升落的先后关系以及月亮在夜空中出现的位置和停留的时间就好判断了(图三下面的表有归纳)。说到底,就是你必须正确确定自己的观测点的位置,那样你的观测结果才可能是正确的。
另外要交代的是,照上述方法分析和理解图一,如图中所示都是符合客观实际的话,那么该图反映的就应该是北半球中纬度地区观测的情况。
关于下面图三,这幅图也是默认了观测者是在北半球中纬度地区。上半月和下半月图中都同时画了几个月亮,这也会让一些人迷惑不解。其实交代的是图中各种月相并不是出现在同一天,而是表示不同日期的月亮在太阳升起或落下这两个时刻在天空中的位置及相应的月相。不同的月相是不可能出现在同一天的。
图三
至于上面课本上的《月相同太阳出没的比较,夜晚见月情形》的表格,其内容完全不必死记,那样是愚蠢的,不能理解就难得记,记得一时也难长久。我们需要的是理解的记忆,前面文字已经帮助分析了,此不多说。遇到具体的问题时还要临时推导,这样才能做到准确无误。必要时可自制月相变化演示仪,或做flash动画演示,帮助对上表的理解记忆。
另外,从准确意义上来讲,此表只能反映赤道地区常年的情况或其他地区多年的平均状况,为什么这么说呢?举一例就可证明:例如二至日及其前后一段时间的极点在极夜时,如果是上弦月—满月—下弦月这样的月相,月球在地平面之上,月亮整夜可见,而遇到下弦月—朔月—上弦月的月相,月球在地平面之下,整夜不见月亮。此时处于极昼的另一个极点的情况与之正相反,从月球出没地平面的情况来看,两极点始终是此起彼落的关系,出现的月相完全不同,此时这个极点是下弦月—朔月—上弦月这样月相出现在地平面上,但是极昼时有太阳的光辉照耀,尽管月球有且必定是半个恒星月的时间在地平面之上,人们可能还是不能看初一前后的弯月,接近弦月的月相可能容易看到些。
当然上表中四种月相在中高纬地区的表现与表中所示也会有较大的出入。
还可以进一步探讨,同一时刻的月相,在地球的不同位置观测,月面的朝向也有不同,比如说蛾眉月(或新月或残月)在接近地平线时,在低纬看,月面的凸向是接近或可以朝正下方,在北极点上看,弯月是近乎竖直于地平面上的,尽管我没有到过北极,但这完全可以想象得到,这需要较强的空间想象能力。这就是我在后面面要重点讨论的问题。
这里先引入视夹角的概念,如图四,视夹角即月球迎光面同地平面的夹角,图中α 即视夹角。
2004年12月10日,农历十月 2003年11月26日,农历十一 网友拍摄之上弦月图
二十九黎明前,残月从东方升起。 月初三悬挂在约旦首都安曼一座
曾惠苹摄于井冈山,数码拍摄。 清真尖塔上方的夜空的一轮新月。
二、练习中存在的问题
市面上有关月相练习的题目,很多都有问题。一般都是给你一幅图,图中什么参照物都没有,只有月相,月相可能是弦月,可能是弯月或凸月,让你判断是上弦月还是下弦月,是初三的月亮还是二十七、八的月亮等。(图五,四种情况)
A B C D
问:A和B的半月图,哪一个是上弦月,哪一个是下弦月?
C和D,哪一个是初三的月亮,哪一个是二十八的月亮?
图中没有画出地平线也没有标出地平面上的方向,没有标出观测地点(是哪个半球,哪个纬度范围)。严格说来这样的题目是无法做的。之所以一些题目在资料上有所谓的正确的答案,我想那是他们默认了一切月相都是在北半球中纬度观测到的,且默认了弯月图的下方边框线就是地平线,对于弦月他们默认了图的左边框线是东,右边线是西,上边线为北,下边线为南;对于新月,他们不能默认图的下边框线左、右两边面是北还是南,那就只能服从于月相判断的结果了。对于新月,他们认为右面是北;对于残月,他们认为左面是北,见下面图解
(图五,四种情况) 默认是在北半球中纬度某同一地点观测
上弦月 下弦月 初三 二十八
图中的方向都是默认的,资料上没有标出来,这里我标出方向。
上弦月和下弦月都是仰望天空所见。
三、对月相判断的深入认识(创新部分)
如上所述,我们发现了练习中的问题,那么怎么样解决呢?要尊重客观实际,真正科学的题目是要以全球为考察范围的。在图中要交代地平面、地平面上的方向、月亮在地平面上的高度,观测点的位置(半球位置,纬度位置)等,甚至有必要时还要交代经度位置和观测时具体的地方时刻。知道了上面的几个条件中的其中几个,那么另外几个结果我们就可以推导出来。下面看一个具体的例子:
有一次我在看中央电视台的节目《两极之旅》时无意中发现了一个镜头,即日出前的弯月,当时是摄制组的人员到安第斯山顶去拍摄温泉在日出前的那种云雾蒸腾的样子,以显示温泉热度之高和景象之壮观,当镜头指向黎明前的泛白的东方时,我发现一轮弯月在东方地平线上,弯月的凸面是向右下方凸出的(图六、下右图)。
落基山脉观测 安第斯山脉观测
(图七) (图六)
这使我要思考其道理,很快我明白了其中的道理,我进一步想,假如此时在北美洲的落基山脉看这轮弯月,又是什么样的景象呢?不难理解,在地平线上月面应该凸向左下方(图七,上左图)。我一直在思索和判断在地球的不同的地方观看月亮,月相形状同地平面的相对位置关系是不同的,以前我在课堂上也给学生们讲过这一点,我举的是赤道和北极点对比这个例子,这两点的人站立的角度相差90°,那么他们观测到的位于赤道地方的地平面上东方或西方遥远的接近地平面的物体的视角自然相差90°(见下面原理图,图八)。在图中我们是可以推断出其几何原理的,在电视上看到的镜头进一步证明了我以前的推理,这里可帮助理解上面图六和图七的不同。
赤道所见 北极所见
(图八)
根据同样的原理,我们还可以想象和推断出在地球各地,不同的时刻观测到的各种月相的情况。
但是,在判断前我们要知道如下几点前提条件:
1、 球绕太阳运动的轨道叫黄道,月球绕地球运动的轨道叫白道,白道和黄
道是有一定的交角的,但交角不大(为5°09′),从每个月来看月球有一半的时间在黄道面以下,一半的时间在黄道面以上(准确地说是半个交点月的时间,一个交点月是27.21222日),这样从全月、全年的平均状况来看可以认为月球的位置就在黄道面上,我们可取这个平均值来看问题。
2、同一天,地球各地见到的月相的形状,即盈亏状况是一样的。其原理是对于遥远地方的天体来说,可以认为地球就是一个点。
3、月球的视半径是15分33秒,接近太阳的视半径。
4、当然我们最好还要了解月球距离地球平均为38.4万千米,一个朔望月的周期是29.5306日,一个恒星月周期是27.32日,自转周期也是27.32日,恰好和恒星月周期相同,这决定了月球始终只有一面对向我们地球,即所谓的“正面”,而它的背面我们在地球上是永远也看不到的。
遇到具体问题时具体分析,都可以得到特定的结果,为了叙述上的方便,我们就以上面的4点所说的平均状况来分析问题。为了使问题的说明更具有条理性,我们按春分、秋分、夏至、冬至四个节气分别来谈不同纬度地点所见不同月相的情况,选南、北极,南、北纬45°,赤道,共5个地点来观测,重点选新月(具体到初二或初三),残月(具体到阴历二十八或二十九)。
这样看来,4个时间,5个地点,2种月相,组合起来工有40种不同的观测结果(见图九,组图)。上、下弦月,凸月及满月另外再简单地谈谈。
1, 春分时各地观测月相情况:(准确地说应该是月球位于春分点的情况,余类推)
1, 新月(阴历初二或初三)
南极点 南纬45° 赤道 北纬45° 北极点
(各幅图下边的框线为地平线,除南、北极点外,其
正中的方向为正西方或正东方,下面各组图道理相同)
2, 残月(阴历二十八或二十九)
北极点 北纬45° 赤道 南纬45° 南极点
(凡是新月日,落后出现在西方地平线;凡是残月,日出前出现在东方地平线)
二,秋分时各地观测月相情况:
1, 新月
南极点 南纬45° 赤道 北纬45° 北极点
2,残月
北极点 北纬45° 赤道 南纬45° 南极点
(残月和新月与太阳升落时间都很接近,春、秋分时升落方位是正东正西)
3, 夏至时各地观测月相的情况
1, 新月
南极点 南纬45° 赤道 北纬45° 北极点
(南极点处于极夜,无法见到新月,北极点处于极昼,月球高度接近23°26′,月弓和地平面的夹角为90°。但是极昼时,太阳和新月同在地平面上,能否看到新月,还要视乎当时的情况,前面已有论述,也许初三以后的月亮容易看到些,有待考察。下面几幅极点的图的情况用相同的方法分析)
2, 残月
北极点 北纬45° 赤道 南纬45° 南极点
4, 冬至时各地观测月相的情况
1, 新月
南极点 南纬45° 赤道 北纬45° 北极点
2,残月
北极点 北纬45° 赤道 南纬45° 南极点
(图九,组图)
(注:为了叙述方便和讲清原理,以上都不计较日月细微的黄经差。另外在实际观测中,新月、残月的“月尖”部分由于视直径太小而难以被肉眼看到,不能如图中所画理想状况那样月弓可以达到一个半圆弧)
从夏至和冬至各组图还可看出:夏至时,各地的新月都从西偏北落下,残月都从东偏北升起,基本等同于太阳的升落方向,其天文原因是新月、残月和太阳的黄经、赤纬相差不大。同样的原因,冬至时,各地的新月都从西南落下,残月在东南升起。
以上各图都标明了“月弓”在接近地平面时和地平面的夹角,其理论依据在于要知道当时日、地、月的位置关系,日、月在黄道上的位置。这里我们还要知道月弓的竖直方向与黄道面是垂直的,月球迎光面与地球晨昏圈平面是平行的,这可画立体视图说明。这样,各种情况我们都可画相应的便于观察和分析的视图,从而推算出“月弓”同地平面的夹角。上图中冬、夏至时南、北纬45°地方的夹角50°41′,这要利用球面三角知识求出来,这里就省略画图和公式的推导与计算了。如能用三维动画来演示,效果更好。
通过深入研究,我们发现利用天球仪器来演示不同月相在不同时间的位置,视夹角则更直观。后述各种情况一样,若用天球仪演示更直观。
对于弦月、凸月来讲,我们可以根据上述的原理,用同样的方法推算出它们的视夹角,但是它们的形状看起来更接近“块状”,而不象新月、残月那样接近“条状”,也因为它们不象新月、残月那样只是在日落、日出前后不久出现在地平线上不高的位置,所以研究它们同地平面的夹角“意思”不大或观察时间不方便,更因为考虑到叙述上的不方便,这里只对它们的月相状况作简略讲述。取全球各地的平均位置即赤道在多年的平均月相状况来看(见图十,组图)。又有以下几种情况:
1,上半夜西部夜空上弦月的情况 2,下半夜东部天空下弦月的情况
日落时仰望星空 午夜时西方地平线 午夜时东方地平线 日出前仰望星空
3,十五前的凸月在地平面上的情况 4,十五后的凸月在地平面附近的情况
日落后东方地平线 日出前西方地平线 日落后东方地平线 日出前西方地平线
(上面四个图中“日出前”、“日落后”分别都取极相同的地方时刻,可以看出在相同的地方时刻,十五前后的月亮在地平面上的高度不同。图中所示日出前的地方时刻以十五前的凸月靠近西方地平线为准,日落后以十五后的凸月升上地平面为准,这样才有了上图不同月相的相同地方时刻在地平线上的高度对比)
5,凸月在上中天时的情况
(十五前的凸月,午夜前一点仰望星空, (十五后的凸月,午夜后一点仰望星空,
月面朝西,接近上弦月的情况 ) 月面朝东,接近下弦月的情况)
(可以说十五和初一是月面朝向的一个分水岭)
(图十,组图)
十五的月亮(满月),我们研究所能见到的它的亮面和地平面的夹角关系没有多大的意义。但是我们可研究它升起和落下的方向和时间,以及它到达中天的高度。可以概括地说各地满月的升落方向、升落时间、当夜最大月亮高度角与当日的太阳在上述几个方面的表现密切相关,情况应该是正好相反。比如,北半球夏半年太阳从东北方升起、升起时间必然在6时以前,北半球地区正午太阳高度角就大,傍晚在西北方落下,落下时间在下午六时以后。那么当地当日的月亮是从东南方向升起、升起时间是在下午六时以后,北半球月亮到达上中天时高度角小,在西南方向落下,落下时间是在六时以前。为什么会这样呢?从天文意义上理解其原因,是因为十五的时候太阳的黄经和月球的黄经相差180°,赤纬数值相同,但方向正好相反,一个在北赤纬,那么另一个必然在南赤纬。也可通俗地理解其带来的结果:十五的月亮和太阳的关系是“此升彼落”即“你东我西”的关系,当然还有“你北我南”、“你早我迟”和“你高我低”的相反或对称关系。
其他的情况可类推。
所以要详尽研究月球与太阳的升落时间关系、月球的上中天高度,那还要看当日它们之间的黄经差,各自的赤纬数等。
理解了上述原理我们还可以回答这样的问题:俗语说“月到中秋分外明”,那么中秋的月亮是一年中最明亮的吗?
通过长期的观察和分析,我们认为“月到中秋分外明”这只是诗人,文学家的语言。实际上中秋的月亮不是一年中最明亮的,为什么呢?要回答这个问题还是先从对我们本月的观测结果分析开始。我们还记得今年(2005年)9月13号夜晚8点半左右我们看到的上弦月的上中天高度只有45°左右,而到了二十二、三,黎明时月亮高度可近90°,这样看来月球在不同的时候能达到的上中天高度也是不一样的。(观测地点:顺德一中,北纬22°50′)
我们可画图分析:选秋分日恰好为上弦月的特殊情况,如下图:(图十一)
白道(此图中为月球真运动轨迹)
月球一个月在白道上走一圈
黄道(太阳视运动轨迹)
太阳一年在黄道上走一圈
此图反映的是本月月相为上弦月时的日、月相对位置。从图中可看出,九月份的太阳落在秋分点附近,月相为上弦月时,月球必然落在图中所处A点的位置,对应于黄道上冬至点的位置。这里须交代一下,月球绕地公转的轨道叫白道,白道面与黄道面不在同一个平面上,但它们之间只有一个很小的夹角为5°09′,为了研究月相的方便,此处我们可以近似地认为白道与黄道在一个平面上(准确的计算月球赤纬则还要考虑黄赤交角和黄白交角的叠加,月球赤纬最大可达28°多),所以此图中上弦月的位置对应于黄道上的冬至点,月光直射点在南回归线附近,这样我们在北半球看月球上中天的高度就很低了。本月的下弦月时,月球落在图中B点附近的位置,对应于夏至点,月光直射在北回归线附近,月球上中天的高度自然就高了。观测结果确实是这样。
一年中什么时候月亮最明亮呢?除了月要圆之外,还要月亮的上中天高度最大,要满足上中天高度最大,月球必须在夏至点附近,对于北半球而言,此时月球赤纬最大,而此时要满足月最圆的条件须是农历十五,这时候只有太阳落在冬至点附近才行,即是冬季的十五月亮最明亮。这样看来“月到中秋分外明”就不能说是全年中最明亮的了。
又比如说2003年全国天文奥林匹克竞赛低年组卷里有这样一道题目:
月亮绕地球公转的轨道平面和黄道只有一个非常小的夹角。请问,上弦月发生在一年的什么时候(比如几月份左右),在上中天时可以有最大的地平高度?(假设你在北京观测)。
用同样的方法可推断出:上弦月上中天的地平高度极大值的时期是春分时的上弦月,但是不可能每次春分时恰好为上弦月,所以答案应该是三月份左右的上弦月。
由此还可推导:对于北半球回归线以北地区来说,秋分时上弦月地平高度最小,下弦月的情况与此正相反。还可推导夏至时满月的中天高度达到最小。
以上是定性的分析,也需要较强的空间思维能力。如有了一定的天文、数学基础知识的话,我们还可用相关的公式来计算,这要用到球面三角理论。
不论是求月面与地平面的视夹角,还是求各月相的上中天高度,前面我们举的春、秋二分,冬、夏二至都是特殊的情况,各节气又刚好对应新月、残月,或上、下弦月就更特殊了。事实上不可能每次情况都和上述的相对应,即在上述节气不可能每次都是初二、三,或初七、八,十五,二十八、九等,这时候就要求考虑非特殊的情况了。比如说2004年3月20日是春分,当日是农历三十,这样节气与新月的出现是很对应的,可以套用前面的组图八来分析。而2004年4月22日农历初四不属于二分二至节气,当日夜晚天气好,我用双筒望远镜观测了西部天空,看到金星之下是一轮明亮纤细的弯月,在它将接近地平面时与地平面只有很小的夹角,看起来几乎是平行于地平面。具体夹角是多少呢?这需要用公式计算,因为前面我也说过月球的亮面和黄道面始终是垂直的,所以我们只要求出当日月球到达地平面时,黄道面与地平面的二面角就行了。
我所在的广东佛山市顺德区一中纬度是北纬22°50′,地平面与赤道面的交角为67.17°。当日太阳的黄经是在春分点以东约(33日/365.2422日)*360°=32.526°,初四月亮接近地平面时为晚上8时30分左右,所以月球与太阳的黄经差为 (3.85日/朔望月29.53日)*360°=46.935°(这里默认了初一零点时月球与太阳黄经相同,具体数据查天文年历更准,这里重点突出计算方法),落在太阳以东,所以月球的黄经为上述两式数值之和,约为79.46°,比较接近夏至点。当月球刚好落在西部地平面上时,黄道、赤道、地平圈共同组成了一个相应的球面三角形,在这个三角形中可求出黄道面和地平面的交角。经过一系列复杂的计算,得知交角为69.63°,黄道面向南倾,所以月面与地平面的夹角就是69.63°的余角 ,为20.37°,向北倾(见图十一),可以看出这个倾角是很小的。同一日,北京地方的弯月与地平面的夹角也可计算出来约为49°,倾角明显大于低纬所见。
广东佛山市顺德一中所见 北京地区所见
图十二
用此方法还可求出任意日期里月面与地平面的视夹角。可以概括性地说,也是一个重要的原理:月球落在地平面上时,月面(即所见迎光面部分,或弯月或凸月)与地平面的视夹角都等于当时当地黄道面与地平面夹角的余角或补角。地平面与黄道面的夹角随着地球的自转又在不断地变化,也许我们可以推导出此夹角在一日内随时间变化的函数表达式。在特定黄道位置上的月亮在某日内一定会在特定的时间落在地平面上,利用函数式我们可以即时求出月面与地平面的视夹角。月球在其它地平高度时,视夹角则需要更为复杂的计算才能求出,进一步推导,我们也可得出相应的公式,只要有了一定的参数,其它地平高度的视夹角都是可求出来的。如何计算,另可见我写的文章《在天文观测中推求球面三角关系》,此不细述,容后分析解答。
月相判断看似复杂,但也有规律可循,还可以补充和归纳以下几点:
①月相盈亏的多少决定于它距初一或十五的远近,或是它与太阳黄经差的大小。月相盈亏的多少也决定了月亮在夜空中停留时间的长短,成正相关。
②弯月和凸月的外圆弧长都始终等于180°。从几何意义上看,这还可以帮助我们画出正确的月相。“外圈”为半圆弧,“另一半”是长轴等于月球直径的半个椭圆弧。(如图十三)
③月亮盈亏多少相同的情况下,到底是十五前,还是十五后的月亮,则要看当时月面的朝向了。是在哪个半球,哪个纬度观测的则要看相应时刻月面与地平面的视夹角及月面的倾向了,如前述各组图。
④从多年平均状态来看,各种月相落入地平面时其视夹角北半球向北倾斜,南半球向南倾。不论南、北半球,纬度越高,倾角越大。无论哪种月相,其“视夹角”多年平均等于当地的纬度值。赤道地区多年平均无倾角。
又深入分析和论证第④点,多年平均,各种月相落入地平面时,视夹角应该等于当地的纬度值。就拿赤道地区的上弦月这种特殊情况来看吧(如图十四)
夏至 春分 秋分 冬至
图十四
绘此图的基础是要知道上弦月与太阳黄经相差90°且落在太阳以东,
另外要保证日、地、月都在黄道面上,保证黄赤交角为23°26′。)
此时赤道上的A点是午夜,月亮正落入到西方地平面,夏至时其与地平面的夹角为北倾23°26′,方位正西;春分时夹角0°,方位西偏北;秋分时夹角0°,方位西偏南;冬至时夹角南倾23°26′,方位正西。这样从全年平均来看,上弦月是从正西落下的,弦月面与地平面夹角平均为0°,即等于赤道的纬度0°。
另外拿北纬45°地区的新月来看,参看前面组图九,从春分—夏至—秋分,夹角是由最小到最大,即由21°34′到68°26′,平均起来等于45°,即当地的地理纬度。从秋分—冬至—春分,又从最大到最小。巧的是冬、夏二至时夹角相同,都为50°41′,但是落下的方位不同,夏至在东北方落下,冬至在西南方落下。
以上也只能算是定性加简单定量分析和论证,因为也只是取了特殊的情况。
还可以进一步定性分析论证:某月相每月出现一次,各月该种月相在黄道上的位置不同,但是多年来看,它可均匀地分布在黄道上的任何位置。而地平面同黄道面的夹角每天(严格来说是一个恒星日)变化一个周期,从全天夹角的平均值来看,等于当地纬度的余角值,这有待建立数学表达式。这里不考察每天的情况,考察的是上述月相每月一次落在地平面时的“黄地”夹角,其各月也在变化,但多年平均也应该等于当地纬度的余角值,即全天的平均值。月面与黄道面始终是垂直的,所以月面与地平面的平均视夹角多年平均就等于“黄地”夹角的余角值,即当地的纬度值了。目前的分析和论述只能到此,关于其它地平高度的平均情况更不是一时半会儿说得清楚的,如前面文字所述,有必要时要建立一个数学模型,考察其视夹角的时刻变化。
用数学方法来证明上述第④点结论,还需要较大的篇幅,我想公式的推导和结果也应该是十分美妙的。
月相判断,如只想粗略了解,难度并不大,但要深入研究,则难度并不小。通过深入研究,能丰富我们的天文知识,增强空间想象能力,其教育内涵是极其丰富的。
本文第一部分主要从学习的角度来讲,本想更简洁一些,但还是略显罗嗦,但这部分是基础,是对解决后面问题的铺垫。其实有很多人写过关于这部分内容的文章,方法多种多样,各有千秋,不可拘泥于一种形式。文章第二、三部分则是对月相及相关问题的深入分析,是本文的重点。
本文力求用通俗的语言讲清一些浅显的道理,同时又不回避难点问题,敢于深入挖掘和拓展研究,重点研究了月面与地平面的夹角和观测地点、观测时间的对应关系,主要月相上中天的高度和月份、日期,观测地点的对应关系等。很多问题先从定性的角度去讲并用实例予以佐证,最后上升到定量分析的高度,这也是我要追求的效果。深入研究,则不可避免地要用到了数学中的球面三角知识,有些特殊情况可直接导出结论,如组图九,主要靠的是空间想象力和简单的计算,就没有用繁琐的数学公式表达了。但是在考察非特殊情况的时候就要用到复杂的数学计算了,这需要较强的数学能力。
研究月相问题或是其它天文问题,需要较强的空间思维能力,本文用了较多的图解,能否从正确的角度去看图也是理解本文的关键所以在。
本文力求全面解答月相有关问题,但是要说明各种具体的情况,短短的篇幅是做不到的,在实际研究中还要详细取得各种参数,才能得到精确的结果。
刘华新
2003年九月初稿
美月欣赏:
趣味分析:
上图能清楚地看到弯月和地平面的夹角关系。根据前述理论,如果是在北半球拍摄的,月弓向右倾,那应该是新月。反之,知道了是新月,那应该是在北半球拍摄的,这有必然的对应关系。如果是在南半球拍摄的,那应该是残月。残月必然要在凌晨拍摄,但又有谁会在黎明前出来小坐并溜狗赏月呢?所以这幅照片多数可能是在日落后北半球某地拍摄的。
进一步看,地平线上枯枝落叶或嫩芽初发的植被景观,显示着这更可能是在较高纬度的秋冬或冬春季节拍摄的。弯月呈白色,而不是呈红色,这说明近地平面上水汽较少,这在较高纬度更加明显,这可能也是一个证明。既然是在较高纬度,根据前面的推算,如果是秋季,新月位于秋分点附近,那时的视夹角是最大的,可达到60°以上,但是目测照片中月亮的视夹角却不大,不到45°,根据前述分析,月球位于春分点时才有这种可能。当新月位于春分点附近,太阳也应在春分点附近,季节为春天。所以这幅图很可能是在冬末或春初拍摄的。
再看这植被类型,怎么看都不像是欧洲的,所以可能是在欧洲以外的季风气候区气候区拍摄的。
如果知道了拍摄的具体日期,我们可以推知拍摄地纬度。反之,如果知道了具体的拍摄地点,我们也可以推出拍摄的日期。
照片中月弓同地平面的大致夹角是可目测出来的。
新月抱旧月:
上图所展示的是一种俗称为“新月抱旧月”的现象,一弯新月怀抱中隐约可见的暗灰色光实际是地球反射的太阳光照到月面上又反射回来的光。上图是天体摄影家laurent laveder从pic du midi天文台拍摄到的
这幅图是在Pic du Midi天文观测台拍摄的
The Pic du Midi Observatory is located at an altitude of 2890 meters (9470 feet) on an isolated summit of the Pyrénées range which separates France from Spain.
( Pic du Midi天文观测台是位于将法国和西班牙分开的比利牛斯山脉的一座海拔2890米,即9470英尺的孤立的山峰上。)
从地图上看比利牛斯山脉的位置,该天文台纬度大致是北纬43度左右,北半球弯月月面向右倾斜必然是新月。从月面的盈亏来看像是初四、五左右的月亮,图中看不到地平面,如果摄影家是朝水平方向拍摄的,可以看出月面同地平面的夹角较大,大概能达到67度。根据前述原理分析,这张照片应该是秋分前后拍摄的。
这幅图及资料介绍来源于网址:
http://webast.ast.obs-mip.fr/patrimoine/asp.html
附:原理图:
1. 春分
新月 残月
2. 秋分
新月 残月
3. 夏至
新月 残月
4. 冬至
新月 残月
以上各图始终都保持黄道面和赤道面的交角为23度26分
5.月球迎光面和黄道面的关系:月球迎光面始终垂直与黄道面
6. 2004年4月22日,月球落在北纬22°50′ 的西部地平面上A时,黄道面、赤道面和地平面组成的球面三角图:ABC组成球面三角形,B是春分点,C是地平圈与天赤道的交点(西点)。
设AB弧为c,c=79°28′,设AC弧为b、BC弧为a,
已知∠B = 23°26′ 、 ∠C = 67°10′ 求出∠A 。
先根据正弦公式 可求出sinb = 0.42 、 cosb = 0.90752
又根据余弦公式
代入已知数到上两式所组成的二元一次方程组,可得:
求出sina≈1
再将它代入正弦公式(或)中
sinA =
A = = 69°38′或110°22′
角A实为钝角,即等于110°22′
但在地平面以上黄道面则向南倾,倾角则为110°22′的补角 69°38′
月弓(即月球迎光面)在地平面上的倾角为90°- 69°38′ = 20°22′
文章后记:
本文于2003年九月就完成初稿,形成了基本的思想,2004年6月在广东省天文学术讨论会上宣读,获得好评。但是文章并没有在一些杂志上发表,自己也没有刻意追求这一点,主要是考虑到文章还有很多表述上的不成熟,自己又没有足够的时间来做这一工作,所以就拖了很长时间。随着时间的推移,文章的时效性就在变化,同时我新的想法也不断涌现,所以每隔一段时间又觉得有必要修改,使文章的时效性更强和表述上更合理,更简洁一些。
在最开始写文章时,我并没有接触到相关的天文软件,后来接触到了一些好的天文软件,我在文章所写的,天文软件都能很好地演示,而且能证实我所写的都是正确的。这样看来我好象是做了一件“多余”的罗嗦的工作,天球仪我早有接触,也有一个,用天球仪也能很好地说明我所写的一些道理。看似多余,但是我觉得有必要,有收获。要说有什么收获,那就是看起来很直接的结果,我从理论上加以了推导和证明。打个比方,知道了直角三角形的两个直角边,那斜边等于多少呢?最直接,最“粗鲁”的方法就是拿一个直杆套上去当斜边,然后把直杆取下来,用尺一测量,就知道斜边等于多少。方法虽然粗鲁,但是效果却是最好的。那至此就不研究了吗?斜边更长的时候,你找不到那么长的直杆怎么办呢?所以必须找到计算的方法,上升到理论高度。我这里想说的就是天文软件或天球仪器虽然方便,但不能代替一切。再说只有弄懂了基本原理,你才能更好地理解和使用软件。当然使用天文软件和天球仪也让我明白了一个道理,那就是凡事能简洁就尽量简洁,哪怕是复杂的理论推导,因为繁琐不是科学,科学应该尽量简洁明了,而只有对一个问题理解最深刻全面时,才能达到简洁的境界。
写这篇文章让我收获不小,要深入研究月相就必然要涉及到天球坐标,还有球面三角知识,为此我专门研究了球面三角,并于2004年4月完成了《在天文观测中推求球面三角关系》,用比较独特的方法证明了球面三角的正弦、余弦定理。参加我的“月相问题研究性学习”小组的学生也有不小的收获,他们完全理解了相关问题,在天文观测和数学上学到了很多的东西,可以说完成了这一课题,他们的天文观测已基本入门了。学生有收获,老师也感到欣慰。
文章倾注了我大量的心血,这倒不是说基本问题的思考和主要思想的形成费神,而是在语言的反复推敲,版面的控制以及绘图上花了我太多的时间,这里要特别说一下绘图的问题,文中本应还有一些通俗的,生动的图的,但是我不会画。就算文中已画的图也没有画好,电子版的图我无法画好,如“原理图”中的地球要画出昼夜半球才便于让人理解,等等。文章需要给人看时我就打印文章,再手工填绘好图,复印给人看。
写这篇文章事实上我扮演了几角色:一是地理教师,要想法让学生更容易地理解课本上的基本知识;二是研究者,力求有所创新,有所发现;三是科学普及者。要说真有什么大的发现,实不敢当,所以我更愿意认为我是在做一点科学普及工作,普及一些最基本的天文知识。我现在不好把这篇文章归为哪一类,这也是一些专业取向很强的杂志不好发表我这篇文章的原因。现在文章只好这样了,基本保持其本质和原貌,那读者就各取所需要吧,现我把文章发给有关的杂志、网站和专家、个人,望共同探讨,并希望各位专家、学者、个人多提意见。
2006年8月
北南
东南
北倾50°41′
竖直90°
南倾50°41′
水平0°
南拿
北南
西南
北倾50°41′
南倾50°41′
水平0°
竖直90°
北
南
东南
水平0°
南倾50°41′
北倾50°41′
竖直90°
北南
南南
西南
南倾50°41′
竖直90°
北倾50°41′
北南
南南
东南
北倾21°34′
左倾66°34′
南倾23°26′
南倾68°26′
倒转左倾66°34′
北南
西南
南南
左倾66°34′
北倾23°26′
北倾68°26′
倒转左倾66°34′
南倾21°34′
南南
北
东
南倾21°34′
右倾66°34′
北倾23°26′
北倾68°26′
倒转右倾66°34′
西南
北
南
右倾66°34′
北倾21°34′
倒转右倾66°34′
南倾23°26′
南倾68°26′
北极
南极
正前为东方
北
南
赤道
南
南
南
北
南
北
东
西
北
北
黄道面
A
A
A
东
西
O
C
B
A
赤道地区,
新月水平落下
方位西南
赤道地区,
残月水平升起
方位东南
赤道地区,
残月水平升起
方位东北
赤道地区,
新月水平落下
方位西北
南回归线地区,新月水平落下
北回归线地区,残月水平升起
虚线和箭头表示黄道及地球公转运动方向,阴影部分为夜半球,下同
只有北回归线地区,新月水平落下
只有南回 归线地区,残月水平升起
水平0°
北拿
东拿
西拿
南拿
北拿
东拿
西拿
南拿
东拿
西拿
北拿
北拿
西拿
东拿
西拿
东拿
南拿
南拿
西拿
西
南拿
北
南拿
北
北倾20.37 °,位置西偏北
北倾49 °,落下晚
北京所见月亮倾角更大,落下时位置更靠西北。
PAGE
14
