1.2 解三角形的应用举例 课件 18张PPT
文档属性
| 名称 | 1.2 解三角形的应用举例 课件 18张PPT |  | |
| 格式 | zip | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-27 20:18:42 | ||
图片预览



文档简介
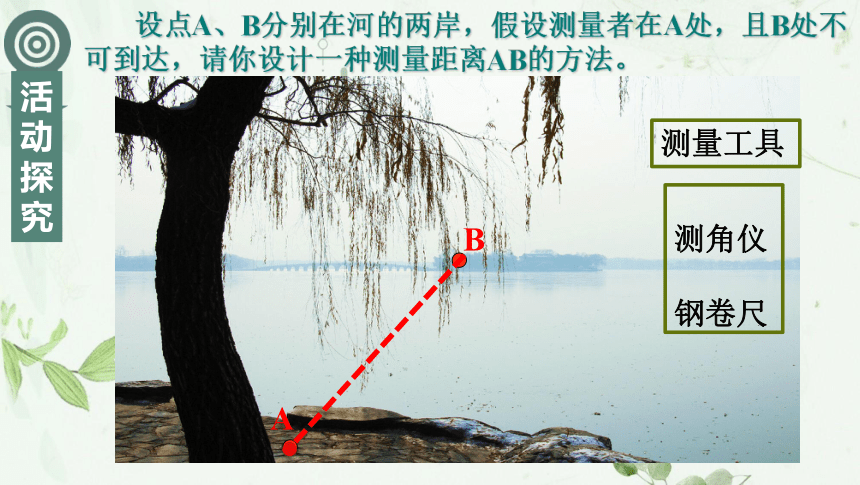
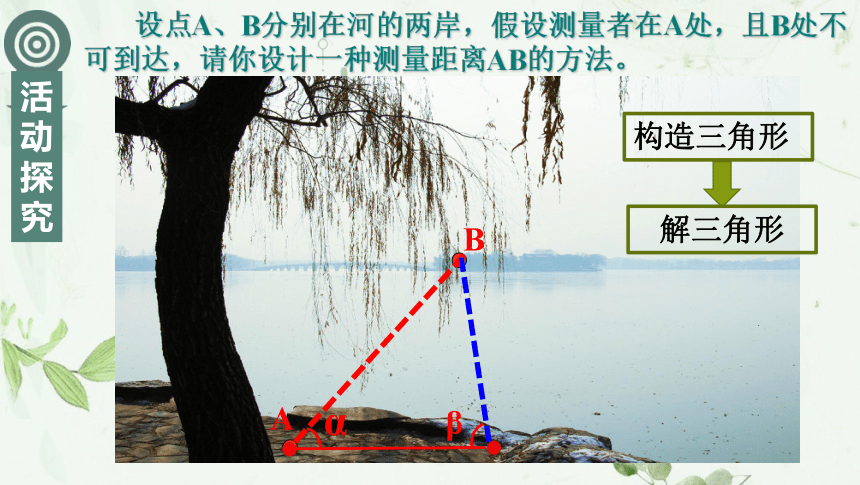
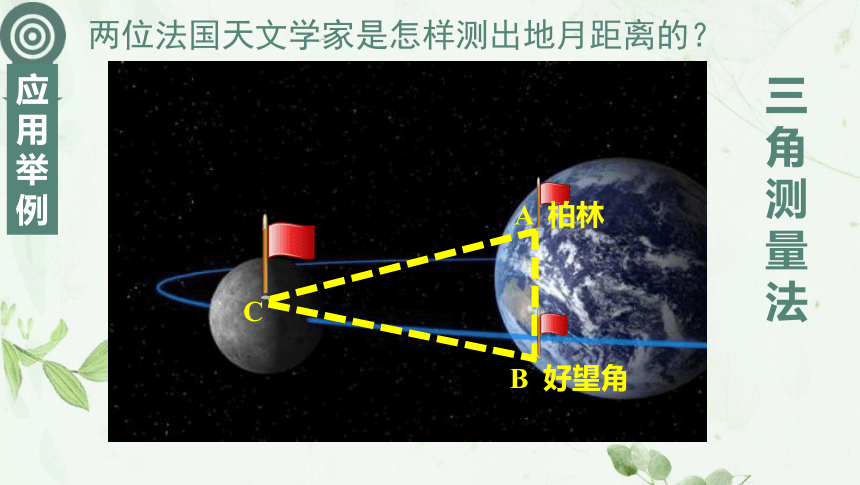
课件18张PPT。应用举例的解三角形1671年,两位法国天文学家测出了地球与月球之间的距离大约为38.5万km,他们是怎样测出两者之间距离的呢?拉卡伊拉朗德38.4万kmAB 设点A、B分别在河的两岸,假设测量者在A处,且B处不可到达,请你设计一种测量距离AB的方法。测量工具测角仪
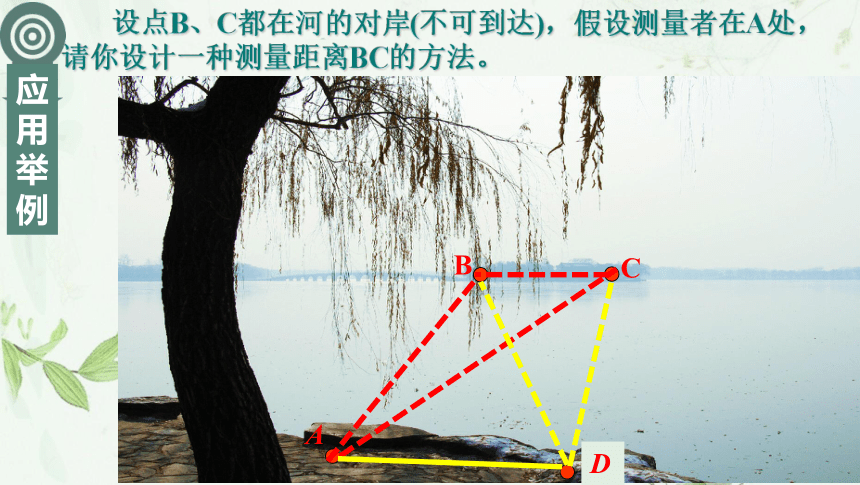
钢卷尺AB 设点A、B分别在河的两岸,假设测量者在A处,且B处不可到达,请你设计一种测量距离AB的方法。αβ构造三角形解三角形正弦定理可解决的两类问题: (1)已知两角和任一边,求其它两边和一角;(2)三角形任意两边及其中一边的对角,求其它边和角.余弦定理可解决的两类问题: (1)已知两边和夹角,求其它两角和一边;(2)已知三边,求三角.两位法国天文学家是怎样测出地月距离的?三角测量法CB 设点B、C都在河的对岸(不可到达),假设测量者在A处,请你设计一种测量距离BC的方法。ABC 设B、C两点都在河的对岸(不可到达),假设测量者在A处,请你设计一种测量距离BC的方法。把未知距离BC转化为求三角形边长问题正弦定理在?ACD中求出AC余弦定理BC60o40在岸边测出AD=40m,∠BAC=60o,∠CAD=45o,
∠ADB=30o,∠BDC=60o,求B、C两点间的距离.例.设B、C两点都在河的对岸(不可到达).例.在岸边测出AD=40m,∠BAC=60o,∠CAD=45o,
∠ADB=30o,∠BDC=60o,求B、C两点间的距离.BC60o401.分析:理解题意,画出示意图。2.构造三角形:把已知量与求解量集中
在一个三角形中。3.求解:运用正弦定理和余弦定理,有顺序地解
三角形,求得三角形的元素。4.下结论:结合实际意义得出实际问题的解。 解三角形应用题的一般步骤是:建模 2012年1月当地时间13日晚,意大利一艘名为“科斯塔·康科迪亚”号的豪华游轮正在进行环地中海旅程,但在行驶至意大利季略岛附近时触礁搁浅。一艘游轮以32海里/小时的速度向正北航行。在A处看岛S在游轮的北偏东15o的方向,若30 min后航行到B处,在B处看岛在游轮的北偏东60o的方向,已知该岛周围6海里范围内有暗礁,这艘游轮可以继续沿正北方向航行吗?解:∵在△ASB中,∠ASB=60o-15o=45o
∵ AB=0.5×32=16 (海里)
∴由正弦定理可得答:这艘游轮不可以继续沿正北方向航行.d一游轮遇险后发出求救信号,在遇险点A处南偏西45o方向10海里的B处有搜救艇收到求救信号后立即侦查,发现游轮的航行方向为南偏东75o正以9海里/小时的速度向一小岛靠近。已知搜救艇的最大速度为21海里/小时。为了在最短时间内追上游轮,求搜救艇在C处追上游轮所需的时间。数学模型这节课我们解决了什么问题?把实际问题转化为数学问题,即数学建模思想。 如何解决?测量距离问题1.铅球场地应用了什么解三角形知识?
2.如何测量底部不可到达的建筑物的高度?思考题FIGHTING谢谢大家2019
钢卷尺AB 设点A、B分别在河的两岸,假设测量者在A处,且B处不可到达,请你设计一种测量距离AB的方法。αβ构造三角形解三角形正弦定理可解决的两类问题: (1)已知两角和任一边,求其它两边和一角;(2)三角形任意两边及其中一边的对角,求其它边和角.余弦定理可解决的两类问题: (1)已知两边和夹角,求其它两角和一边;(2)已知三边,求三角.两位法国天文学家是怎样测出地月距离的?三角测量法CB 设点B、C都在河的对岸(不可到达),假设测量者在A处,请你设计一种测量距离BC的方法。ABC 设B、C两点都在河的对岸(不可到达),假设测量者在A处,请你设计一种测量距离BC的方法。把未知距离BC转化为求三角形边长问题正弦定理在?ACD中求出AC余弦定理BC60o40在岸边测出AD=40m,∠BAC=60o,∠CAD=45o,
∠ADB=30o,∠BDC=60o,求B、C两点间的距离.例.设B、C两点都在河的对岸(不可到达).例.在岸边测出AD=40m,∠BAC=60o,∠CAD=45o,
∠ADB=30o,∠BDC=60o,求B、C两点间的距离.BC60o401.分析:理解题意,画出示意图。2.构造三角形:把已知量与求解量集中
在一个三角形中。3.求解:运用正弦定理和余弦定理,有顺序地解
三角形,求得三角形的元素。4.下结论:结合实际意义得出实际问题的解。 解三角形应用题的一般步骤是:建模 2012年1月当地时间13日晚,意大利一艘名为“科斯塔·康科迪亚”号的豪华游轮正在进行环地中海旅程,但在行驶至意大利季略岛附近时触礁搁浅。一艘游轮以32海里/小时的速度向正北航行。在A处看岛S在游轮的北偏东15o的方向,若30 min后航行到B处,在B处看岛在游轮的北偏东60o的方向,已知该岛周围6海里范围内有暗礁,这艘游轮可以继续沿正北方向航行吗?解:∵在△ASB中,∠ASB=60o-15o=45o
∵ AB=0.5×32=16 (海里)
∴由正弦定理可得答:这艘游轮不可以继续沿正北方向航行.d一游轮遇险后发出求救信号,在遇险点A处南偏西45o方向10海里的B处有搜救艇收到求救信号后立即侦查,发现游轮的航行方向为南偏东75o正以9海里/小时的速度向一小岛靠近。已知搜救艇的最大速度为21海里/小时。为了在最短时间内追上游轮,求搜救艇在C处追上游轮所需的时间。数学模型这节课我们解决了什么问题?把实际问题转化为数学问题,即数学建模思想。 如何解决?测量距离问题1.铅球场地应用了什么解三角形知识?
2.如何测量底部不可到达的建筑物的高度?思考题FIGHTING谢谢大家2019
