华师大版初中数学九上 25.1 在重复试验中观察不确定现象 课件(15张ppt)
文档属性
| 名称 | 华师大版初中数学九上 25.1 在重复试验中观察不确定现象 课件(15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-28 08:15:16 | ||
图片预览





文档简介
课件15张PPT。第25章 随机事件的概率动动脑 有一枚正方体的骰子,抛一次,“骰子的点数不大于6”是否一定会发生?大于6呢?在每次试验中都一定会发生的事件叫做必然事件.在每次试验中都一定不会发生的事件叫做不可能事件.试一试你能例举两个下列事件的实例吗?试一试.
必然事件:
不可能事件:(1)太阳从东边升起.(2)一周有7天.(1)在装了10个红球的口袋中摸出一个白球.(2)两个负数的商小于零.动动脑 (1) 有一枚正方体的骰子,抛一次,“骰子的点数是奇数”是否一定会发生?
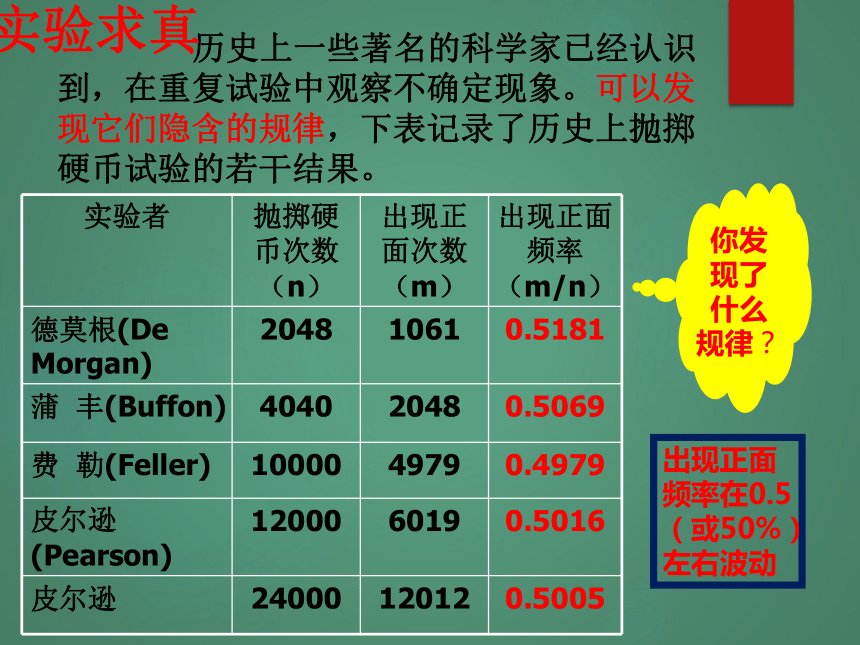
(2)“买一张彩票一定不会中奖”是否一定会发生?无法预先确定在一次试验中会不会发生的事件叫做随机事件.在某一次试验中,可能发生也可能不发生试一试你能例举两个随机事件的实例吗?试一试.(1)抛一枚硬币,正面向上.(2)从一副扑克牌中随意抽取一张牌,这张牌正好是红桃.对应练习1.下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件? (1).抛掷1个均匀的骰子,6点朝上;( )随机事件 (2).1+3>2;( )必然事件 (3).明天会下雨;( )随机事件(4).如果a为有理数,那么|a|<0.( ) 不可能事件 历史上一些著名的科学家已经认识到,在重复试验中观察不确定现象。可以发现它们隐含的规律,下表记录了历史上抛掷硬币试验的若干结果。你发现了什么规律?出现正面
频率在0.5
(或50%)
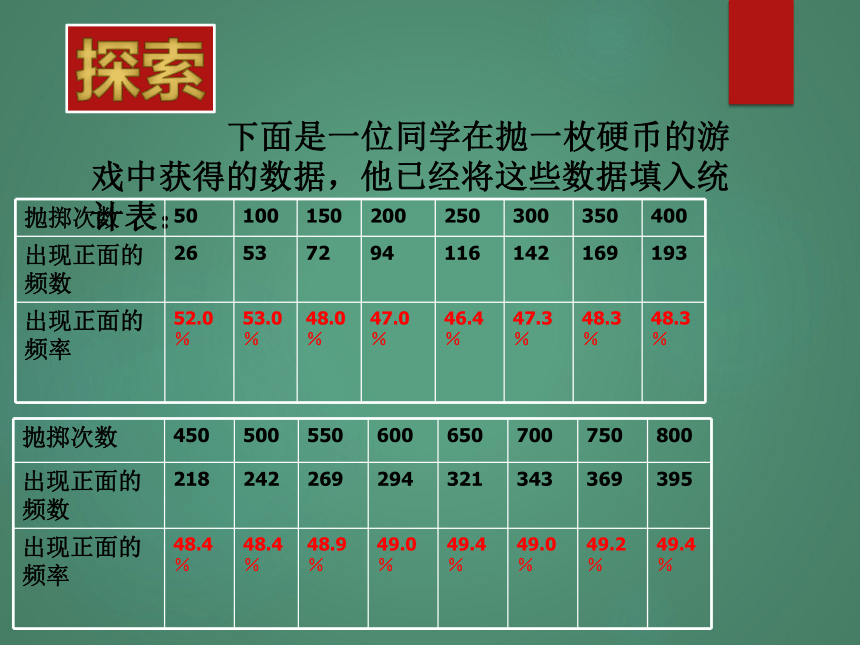
左右波动实验求真探索 下面是一位同学在抛一枚硬币的游戏中获得的数据,他已经将这些数据填入统计表: 根据以上数据绘制出“出现正面”的
频率随抛掷次数变化的折线图:你看到了什么?重新抛掷800次也能看到类似的情况吗?概括 虽然每次出现的结果是随机的,无法预测,
但随着试验次数的增加,隐含的规律逐渐显现:
“出现正面”的频率稳定在50%左右,所以,
我们可以用频率来估计每次“出现正面”发生的
机会的大小为50%. 可以用频率来估计随机事件在每次试验时发生的机会的大小.课堂练习1.(课本127页练习1)下列事件中,哪些是必然事件?
哪些是不可能事件?哪些是随机事件?为什么?
(1)打开电视,它正在播广告;
(2)抛掷10枚硬币,结果是3枚正面朝上与8枚反面
朝下;
(3)黑暗中,我从我的一大串钥匙中随便选中一把,
用它打开了门;
(4)抛掷一枚普通的正方体骰子,抛得的数不是奇数
便是偶数;
(5)我将一粒种子埋在土里,给它阳光和水分,它会
长出小苗.随机事件不可能事件随机事件必然事件随机事件2、下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件? ① 太阳从东边升起 ( ) ② 打开电视,它正在播《新闻联播》;( )③小明将夺得100米冠军;( )④ 在妇幼保健医院里,下一个出生的婴儿是女孩;
( )⑤抛掷1个均匀的骰子,9点朝上;( )⑥用力旋转画有红、黄、蓝、绿四色转盘上的指针,指针会停在黑色上.( )必然事件不可能事件随机事件随机事件随机事件不可能事件课堂练习1.(课本132页练习1)下列是两位同学对抛掷硬币问题
的不同说法,你认为有道理吗?为什么?
(1)抛掷一枚质量分布均匀的硬币,是“正”是“反”
无法预测,全凭运气.因此,抛掷1000次的话也许只
有200次“正”,也许会有700次“正”,没有什么
规律.答:没道理.每次无法预测,但次数增加,是有规律的.(2)抛掷一枚质量分布均匀的硬币,“出现正面”和
“出现反面”的机会均等.因此,抛掷1000次的话, 一定有500次“正”,500次“反”.答:没道理. “出现正面”和“出现反面”的机会均等,并不代表一定有500次“正”,500次“反”.2.(课本132页练习2)某彩票的中奖机会是1%,买
1张一定不会中奖吗?买100张一定会中奖吗?谈
谈你的看法.答:没中奖机会是1%,虽然买1张中奖的机会不大,但还是可能中奖;买100张只能说中奖机会大一点,但也可能不中奖.课堂小结这节课你都学到了哪些内容?确定事件随机事件不可能事件必然事件随机事件中每次试验的结果无法预测,但随着次数的增加,事件发生率一定稳定在一个值左右.可以用频率来估计随机事件在每次试验时发生的机会的大小.
必然事件:
不可能事件:(1)太阳从东边升起.(2)一周有7天.(1)在装了10个红球的口袋中摸出一个白球.(2)两个负数的商小于零.动动脑 (1) 有一枚正方体的骰子,抛一次,“骰子的点数是奇数”是否一定会发生?
(2)“买一张彩票一定不会中奖”是否一定会发生?无法预先确定在一次试验中会不会发生的事件叫做随机事件.在某一次试验中,可能发生也可能不发生试一试你能例举两个随机事件的实例吗?试一试.(1)抛一枚硬币,正面向上.(2)从一副扑克牌中随意抽取一张牌,这张牌正好是红桃.对应练习1.下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件? (1).抛掷1个均匀的骰子,6点朝上;( )随机事件 (2).1+3>2;( )必然事件 (3).明天会下雨;( )随机事件(4).如果a为有理数,那么|a|<0.( ) 不可能事件 历史上一些著名的科学家已经认识到,在重复试验中观察不确定现象。可以发现它们隐含的规律,下表记录了历史上抛掷硬币试验的若干结果。你发现了什么规律?出现正面
频率在0.5
(或50%)
左右波动实验求真探索 下面是一位同学在抛一枚硬币的游戏中获得的数据,他已经将这些数据填入统计表: 根据以上数据绘制出“出现正面”的
频率随抛掷次数变化的折线图:你看到了什么?重新抛掷800次也能看到类似的情况吗?概括 虽然每次出现的结果是随机的,无法预测,
但随着试验次数的增加,隐含的规律逐渐显现:
“出现正面”的频率稳定在50%左右,所以,
我们可以用频率来估计每次“出现正面”发生的
机会的大小为50%. 可以用频率来估计随机事件在每次试验时发生的机会的大小.课堂练习1.(课本127页练习1)下列事件中,哪些是必然事件?
哪些是不可能事件?哪些是随机事件?为什么?
(1)打开电视,它正在播广告;
(2)抛掷10枚硬币,结果是3枚正面朝上与8枚反面
朝下;
(3)黑暗中,我从我的一大串钥匙中随便选中一把,
用它打开了门;
(4)抛掷一枚普通的正方体骰子,抛得的数不是奇数
便是偶数;
(5)我将一粒种子埋在土里,给它阳光和水分,它会
长出小苗.随机事件不可能事件随机事件必然事件随机事件2、下列事件中,哪些是不可能事件,哪些是必然事件,哪些是随机事件? ① 太阳从东边升起 ( ) ② 打开电视,它正在播《新闻联播》;( )③小明将夺得100米冠军;( )④ 在妇幼保健医院里,下一个出生的婴儿是女孩;
( )⑤抛掷1个均匀的骰子,9点朝上;( )⑥用力旋转画有红、黄、蓝、绿四色转盘上的指针,指针会停在黑色上.( )必然事件不可能事件随机事件随机事件随机事件不可能事件课堂练习1.(课本132页练习1)下列是两位同学对抛掷硬币问题
的不同说法,你认为有道理吗?为什么?
(1)抛掷一枚质量分布均匀的硬币,是“正”是“反”
无法预测,全凭运气.因此,抛掷1000次的话也许只
有200次“正”,也许会有700次“正”,没有什么
规律.答:没道理.每次无法预测,但次数增加,是有规律的.(2)抛掷一枚质量分布均匀的硬币,“出现正面”和
“出现反面”的机会均等.因此,抛掷1000次的话, 一定有500次“正”,500次“反”.答:没道理. “出现正面”和“出现反面”的机会均等,并不代表一定有500次“正”,500次“反”.2.(课本132页练习2)某彩票的中奖机会是1%,买
1张一定不会中奖吗?买100张一定会中奖吗?谈
谈你的看法.答:没中奖机会是1%,虽然买1张中奖的机会不大,但还是可能中奖;买100张只能说中奖机会大一点,但也可能不中奖.课堂小结这节课你都学到了哪些内容?确定事件随机事件不可能事件必然事件随机事件中每次试验的结果无法预测,但随着次数的增加,事件发生率一定稳定在一个值左右.可以用频率来估计随机事件在每次试验时发生的机会的大小.
