2019_2020学年高中数学第2章基本初等函数(Ⅰ)2.2.1对数与对数运算(第1课时)对数学案新人教A版必修1
文档属性
| 名称 | 2019_2020学年高中数学第2章基本初等函数(Ⅰ)2.2.1对数与对数运算(第1课时)对数学案新人教A版必修1 |
|
|
| 格式 | zip | ||
| 文件大小 | 328.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-27 22:56:14 | ||
图片预览



文档简介
第1课时 对数
学 习 目 标
核 心 素 养
1.理解对数的概念,掌握对数的性质,能进行简单的对数计算.(重点、难点)
2.理解指数式与对数式的等价关系,会进行对数式与指数式的互化.(重点)
3.理解常用对数、自然对数的概念及记法.
借助指数式与对数式的互化及应用对数的性质解题,培养数学运算素养.
1.对数
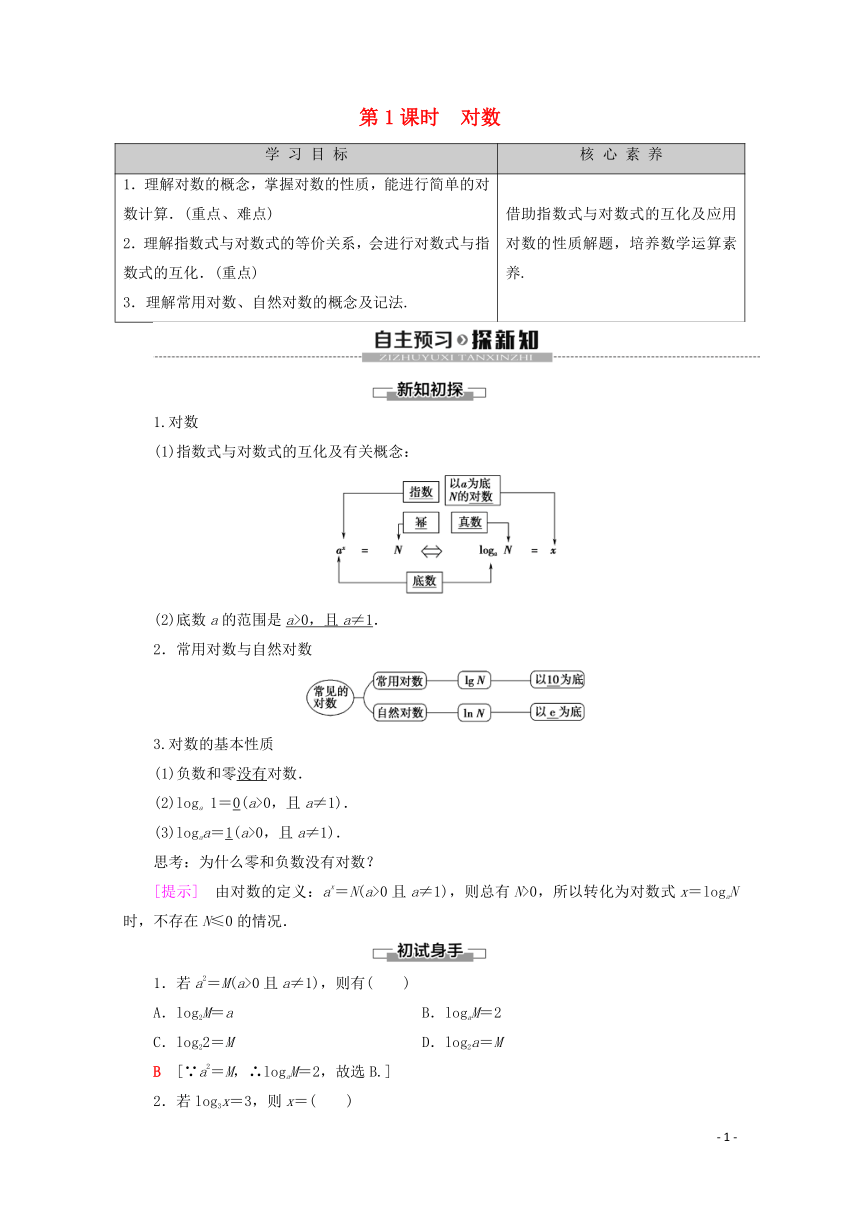
(1)指数式与对数式的互化及有关概念:
(2)底数a的范围是a>0,且a≠1.
2.常用对数与自然对数
3.对数的基本性质
(1)负数和零没有对数.
(2)loga 1=0(a>0,且a≠1).
(3)logaa=1(a>0,且a≠1).
思考:为什么零和负数没有对数?
[提示] 由对数的定义:ax=N(a>0且a≠1),则总有N>0,所以转化为对数式x=logaN时,不存在N≤0的情况.
1.若a2=M(a>0且a≠1),则有( )
A.log2M=a B.logaM=2
C.log22=M D.log2a=M
B [∵a2=M,∴logaM=2,故选B.]
2.若log3x=3,则x=( )
A.1 B.3
C.9 D.27
D [∵log3x=3,∴x=33=27.]
3.在b=loga(5-a)中,实数a的取值范围是( )
A.a>5或a<0
B.0C.0D.1B [由对数的定义可知
解得04.ln 1=________,lg 10=________.
0 1 [∵loga1=0,∴ln 1=0,又logaa=1,∴lg 10=1.]
指数式与对数式的互化
【例1】 将下列对数形式化为指数形式或将指数形式化为对数形式:
(1)2-7=;(2)log32=-5;
(3)lg 1 000=3;(4)ln x=2.
[解] (1)由2-7=,可得log2=-7.
(2)由log32=-5,可得=32.
(3)由lg 1 000=3,可得103=1 000.
(4)由ln x=2,可得e2=x.
指数式与对数式互化的方法
(1)将指数式化为对数式,只需要将幂作为真数,指数当成对数值,底数不变,写出对数式;
(2)将对数式化为指数式,只需将真数作为幂,对数作为指数,底数不变,写出指数式.
1.将下列指数式化为对数式,对数式化为指数式:
(1)3-2=; (2)=16;
(3)log27=-3; (4)log64=-6.
[解] (1)log3=-2;(2)log 16=-2;
(3)=27;(4)()-6=64.
利用指数式与对数式的关系求值
【例2】 求下列各式中的x的值:
(1)log64x=-; (2)logx 8=6;
(3)lg 100=x; (4)-ln e2=x.
[解] (1)x=(64)=(43)=4-2=.
(2)x6=8,所以x=(x6)=8=(23)=2=.
(3)10x=100=102,于是x=2.
(4)由-ln e2=x,得-x=ln e2,即e-x=e2,
所以x=-2.
求对数式logaN(a>0,且a≠1,N>0)的值的步骤
(1)设logaN=m;
(2)将logaN=m写成指数式am=N;
(3)将N写成以a为底的指数幂N=ab,则m=b,即logaN=b.
2.计算:(1)log9 27;(2)log 81;(3)log625.
[解] (1)设x=log9 27,则9x=27,32x=33,∴x=.
(2)设x=log81,则()x=81,3=34,∴x=16.
(3)令x=log625,∴()x=625,5=54,∴x=3.
应用对数的基本性质求值
[探究问题]
1.你能推出对数恒等式alogaN=N(a>0且a≠1,N >0)吗?
提示:因为ax=N,所以x=logaN,代入ax=N可得alogaN=N.
2.若方程logaf(x)=0,则f(x)等于多少?若方程logaf(x)=1呢?(其中a>0且a≠1)
提示:若logaf(x)=0,则f(x)=1;若logaf(x)=1,则f(x)=a.
【例3】 设5=25,则x的值等于( )
A.10 B.13
C.100 D.±100
(2)若log3(lg x)=0,则x的值等于________.
思路点拨:(1)利用对数恒等式alogaN=N求解;
(2)利用logaa=1,loga1=0求解.
(1)B (2)10 [(1)由5=25得2x-1=25,所以x=13,故选B.
(2)由log3(lg x)=0得lg x=1,∴x=10.]
1.在本例(2)条件不变的前提下,计算x的值.
[解] ∵x=10,∴x=10=.
2.若本例(2)的条件改为“ln(log3x)=1”,则x的值为________.
3e [由ln(log3x)=1得log3x=e,∴x=3e.]
1.利用对数性质求解的两类问题的解法
(1)求多重对数式的值解题方法是由内到外,如求loga(logbc)的值,先求logbc的值,再求loga(logbc)的值.
(2)已知多重对数式的值,求变量值,应从外到内求,逐步脱去“log”后再求解.
2.性质alogaN=N与logaab=b的作用
(1)alogaN=N的作用在于能把任意一个正实数转化为以a为底的指数形式.
(2)logaab=b的作用在于能把以a为底的指数转化为一个实数.
1.对数的概念:ab=N?b=logaN(a>0且a≠1)是解决指数、对数问题的有利工具.
2.指数式、对数式的互化反映了数学上的等价转化思想,在涉及到对数式求值问题时,常转化为指数幂的运算问题.
3.对数恒等式alogaN=N,其成立的条件是a>0,a≠1,N>0.
1.思考辨析
(1)logaN是loga与N的乘积. ( )
(2)(-2)3=-8可化为log(-2)(-8)=3. ( )
(3)对数运算的实质是求幂指数. ( )
(4)在b=log3(m-1)中,实数m的取值范围是(1,+∞).( )
[答案] (1)× (2)× (3)√ (4)√
2.下列指数式与对数式互化不正确的一组是( )
A.100=1与lg 1=0
B.27=与log27=-
C.log39=2与9=3
D.log55=1与51=5
C [C不正确,由log39=2可得32=9.]
3.若log2(logx9)=1,则x=________.
3 [由log2(logx9)=1可知logx9=2,即x2=9,∴x=3(x=-3舍去).]
4.求下列各式中的x值:
[解]
学 习 目 标
核 心 素 养
1.理解对数的概念,掌握对数的性质,能进行简单的对数计算.(重点、难点)
2.理解指数式与对数式的等价关系,会进行对数式与指数式的互化.(重点)
3.理解常用对数、自然对数的概念及记法.
借助指数式与对数式的互化及应用对数的性质解题,培养数学运算素养.
1.对数
(1)指数式与对数式的互化及有关概念:
(2)底数a的范围是a>0,且a≠1.
2.常用对数与自然对数
3.对数的基本性质
(1)负数和零没有对数.
(2)loga 1=0(a>0,且a≠1).
(3)logaa=1(a>0,且a≠1).
思考:为什么零和负数没有对数?
[提示] 由对数的定义:ax=N(a>0且a≠1),则总有N>0,所以转化为对数式x=logaN时,不存在N≤0的情况.
1.若a2=M(a>0且a≠1),则有( )
A.log2M=a B.logaM=2
C.log22=M D.log2a=M
B [∵a2=M,∴logaM=2,故选B.]
2.若log3x=3,则x=( )
A.1 B.3
C.9 D.27
D [∵log3x=3,∴x=33=27.]
3.在b=loga(5-a)中,实数a的取值范围是( )
A.a>5或a<0
B.0
解得0
0 1 [∵loga1=0,∴ln 1=0,又logaa=1,∴lg 10=1.]
指数式与对数式的互化
【例1】 将下列对数形式化为指数形式或将指数形式化为对数形式:
(1)2-7=;(2)log32=-5;
(3)lg 1 000=3;(4)ln x=2.
[解] (1)由2-7=,可得log2=-7.
(2)由log32=-5,可得=32.
(3)由lg 1 000=3,可得103=1 000.
(4)由ln x=2,可得e2=x.
指数式与对数式互化的方法
(1)将指数式化为对数式,只需要将幂作为真数,指数当成对数值,底数不变,写出对数式;
(2)将对数式化为指数式,只需将真数作为幂,对数作为指数,底数不变,写出指数式.
1.将下列指数式化为对数式,对数式化为指数式:
(1)3-2=; (2)=16;
(3)log27=-3; (4)log64=-6.
[解] (1)log3=-2;(2)log 16=-2;
(3)=27;(4)()-6=64.
利用指数式与对数式的关系求值
【例2】 求下列各式中的x的值:
(1)log64x=-; (2)logx 8=6;
(3)lg 100=x; (4)-ln e2=x.
[解] (1)x=(64)=(43)=4-2=.
(2)x6=8,所以x=(x6)=8=(23)=2=.
(3)10x=100=102,于是x=2.
(4)由-ln e2=x,得-x=ln e2,即e-x=e2,
所以x=-2.
求对数式logaN(a>0,且a≠1,N>0)的值的步骤
(1)设logaN=m;
(2)将logaN=m写成指数式am=N;
(3)将N写成以a为底的指数幂N=ab,则m=b,即logaN=b.
2.计算:(1)log9 27;(2)log 81;(3)log625.
[解] (1)设x=log9 27,则9x=27,32x=33,∴x=.
(2)设x=log81,则()x=81,3=34,∴x=16.
(3)令x=log625,∴()x=625,5=54,∴x=3.
应用对数的基本性质求值
[探究问题]
1.你能推出对数恒等式alogaN=N(a>0且a≠1,N >0)吗?
提示:因为ax=N,所以x=logaN,代入ax=N可得alogaN=N.
2.若方程logaf(x)=0,则f(x)等于多少?若方程logaf(x)=1呢?(其中a>0且a≠1)
提示:若logaf(x)=0,则f(x)=1;若logaf(x)=1,则f(x)=a.
【例3】 设5=25,则x的值等于( )
A.10 B.13
C.100 D.±100
(2)若log3(lg x)=0,则x的值等于________.
思路点拨:(1)利用对数恒等式alogaN=N求解;
(2)利用logaa=1,loga1=0求解.
(1)B (2)10 [(1)由5=25得2x-1=25,所以x=13,故选B.
(2)由log3(lg x)=0得lg x=1,∴x=10.]
1.在本例(2)条件不变的前提下,计算x的值.
[解] ∵x=10,∴x=10=.
2.若本例(2)的条件改为“ln(log3x)=1”,则x的值为________.
3e [由ln(log3x)=1得log3x=e,∴x=3e.]
1.利用对数性质求解的两类问题的解法
(1)求多重对数式的值解题方法是由内到外,如求loga(logbc)的值,先求logbc的值,再求loga(logbc)的值.
(2)已知多重对数式的值,求变量值,应从外到内求,逐步脱去“log”后再求解.
2.性质alogaN=N与logaab=b的作用
(1)alogaN=N的作用在于能把任意一个正实数转化为以a为底的指数形式.
(2)logaab=b的作用在于能把以a为底的指数转化为一个实数.
1.对数的概念:ab=N?b=logaN(a>0且a≠1)是解决指数、对数问题的有利工具.
2.指数式、对数式的互化反映了数学上的等价转化思想,在涉及到对数式求值问题时,常转化为指数幂的运算问题.
3.对数恒等式alogaN=N,其成立的条件是a>0,a≠1,N>0.
1.思考辨析
(1)logaN是loga与N的乘积. ( )
(2)(-2)3=-8可化为log(-2)(-8)=3. ( )
(3)对数运算的实质是求幂指数. ( )
(4)在b=log3(m-1)中,实数m的取值范围是(1,+∞).( )
[答案] (1)× (2)× (3)√ (4)√
2.下列指数式与对数式互化不正确的一组是( )
A.100=1与lg 1=0
B.27=与log27=-
C.log39=2与9=3
D.log55=1与51=5
C [C不正确,由log39=2可得32=9.]
3.若log2(logx9)=1,则x=________.
3 [由log2(logx9)=1可知logx9=2,即x2=9,∴x=3(x=-3舍去).]
4.求下列各式中的x值:
[解]
