安徽省毫州市涡阳县沪科版九年级上册第22章相似形总复习课课件(共51张PPT)
文档属性
| 名称 | 安徽省毫州市涡阳县沪科版九年级上册第22章相似形总复习课课件(共51张PPT) |

|
|
| 格式 | rar | ||
| 文件大小 | 435.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-27 00:00:00 | ||
图片预览







文档简介
课件51张PPT。相似三角形总复习其中 :a、b、c、d 叫做组成比例的项,线段 a、d 叫做比例外项,线段 b、c 叫做比例内项,比例的性质:知识要点一.比例线段2.比例中项:练习:当两个比例内项相等时,那么线段 b 叫做线段 a 和 c 的比例中项.3.黄金分割:练习:4相似三角形的判定
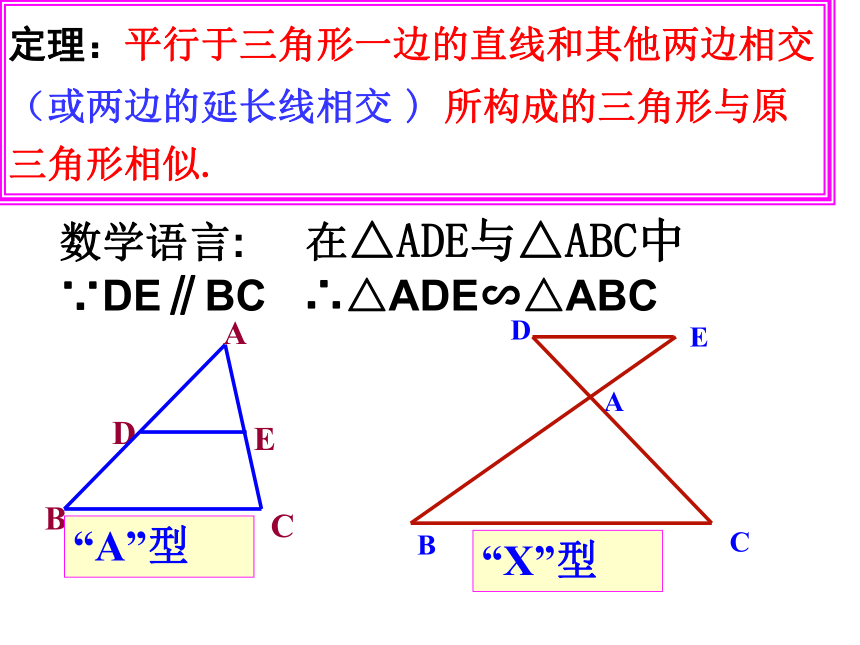
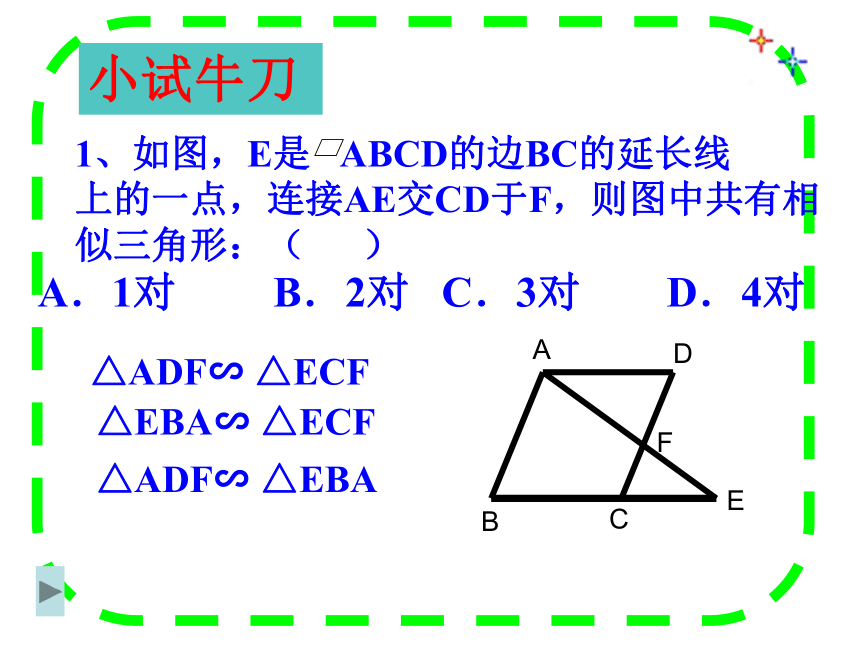
预备定理定理:平行于三角形一边的直线和其他两边相交 (或两边的延长线相交 ) 所构成的三角形与原三角形相似.数学语言: 在△ADE与△ABC中∵DE∥BC ∴△ADE∽△ABC“A”型 “X”型 1、如图,E是 ABCD的边BC的延长线
上的一点,连接AE交CD于F,则图中共有相
似三角形:( )
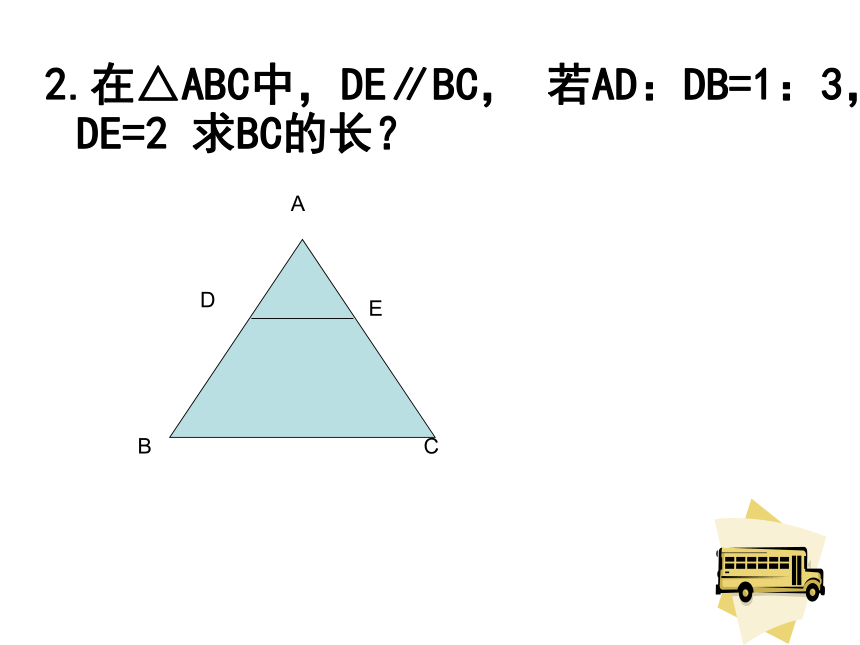
A.1对 B.2对 C.3对 D.4对小试牛刀 △ADF∽ △ECF △EBA∽ △ECF △ADF∽ △EBA 2.在△ABC中,DE∥BC, 若AD:DB=1:3,DE=2 求BC的长?
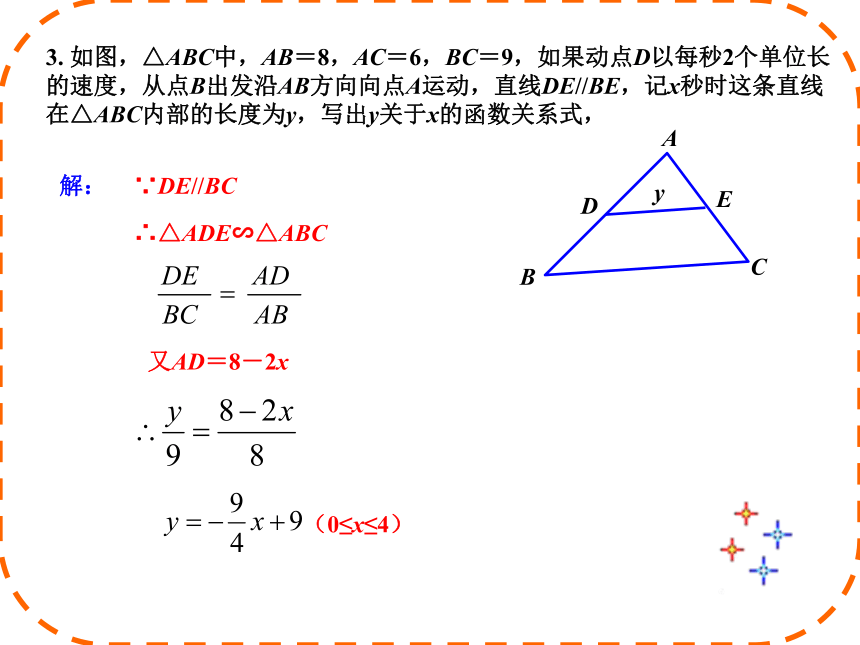
3. 如图,△ABC中,AB=8,AC=6,BC=9,如果动点D以每秒2个单位长的速度,从点B出发沿AB方向向点A运动,直线DE//BE,记x秒时这条直线在△ABC内部的长度为y,写出y关于x的函数关系式,解:∵DE//BC∴△ADE∽△ABC又AD=8-2x(0≤x≤4)相似三角形的
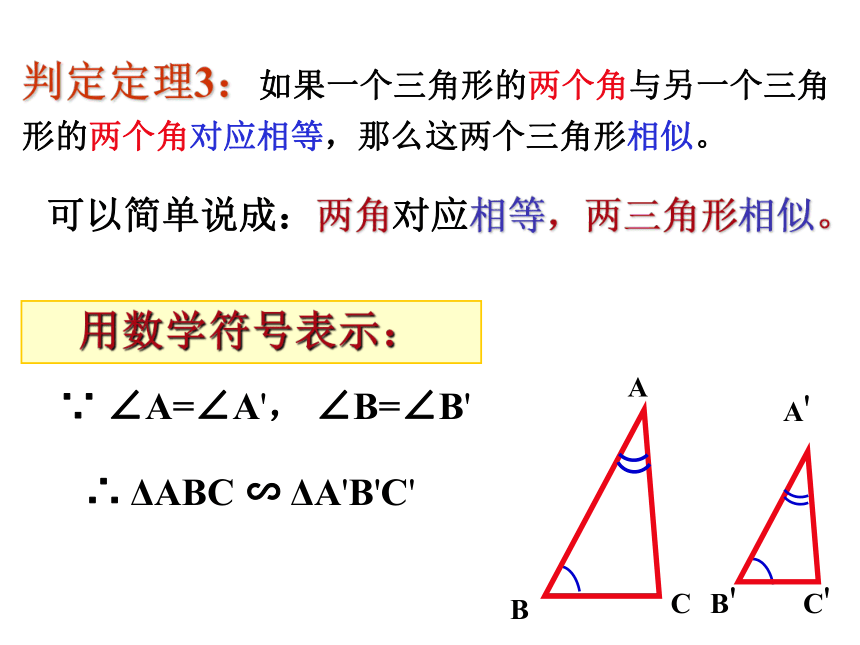
判定AACC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:判定定理3:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。1、判断题:
⑴ 所有的直角三角形都相似 . ( )
⑵ 所有的等边三角形都相似. ( )
⑶ 所有的等腰直角三角形都相似. ( )
⑷ 有一个角相等的两等腰三角形相似 . ( )
×√√×基础演练2、求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,此结论可以称为:“射影定理”,又叫“母子相似定理”∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:(2)AC2=AD · AB (3) CD2=AD · DB
可得(1) BC2=BD · AB DBC3、如图:在Rt △ ABC中 , ∠ABC=90° BD⊥AC于D
② 求证:AB2=AD · AC BD2=AD · DCA 证明 ∵ ∠ABC=900,BD⊥AC
∴ △ ADB ∽ △ ABC
∴AB∶AC=AD∶AB
∴AB2=AD · AC
∵ ∠ABC=900,BD⊥AC
∴ △ ADB ∽ △ CDB
∴ AD∶BD=BD∶DC
∴ BD2=AD · DC
4、如图所示, 锐角△ ABC 的高CD和BE相交于点O,图中与△ ODB相似的三角形的个数有( )
A 1 B 2 C 3 D 45、如图所示,∠ 1= ∠ 2= ∠ 3,∠ C= ∠ E, △ABC 和 △ ADE相似吗?请说明理由。解: △ ABC ∽ △ADE .理由 :
ABCDE 123 ∵ ∠ 1= ∠ 2= ∠ 3,即∠BAC= ∠DAE又∵ ∠ C= ∠ E, ∠ △ ABC ∽ △ADE ∴∠ 1+ ∠ 2= ∠ 2+ ∠ 3,ABCDECOSSS1. 如图,判断两个三角形是否相似,∴△ABC∽△DFC.解:运用2试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAESAS如图:∠DAB=∠CAE且AC×AD=AE×AB
找出与∠ADE相等的角DECBA如图: AB∥CD 求 证:OA·OD=OB·OCABDCO理解4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?这个问题有其他答案吗?4562延伸练习1、已知:如图,在ΔABC中,AD、BE分别是
BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;F答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.2、如图,已知BC∥B'C',AC∥A'C' 求证:△ABC∽△A'B'C' ???????????????????????????? 证明:∵BC∥B’C’ ∴∠3=∠4, B’C’/BC ??= OC’/OC
∵AC∥A’C’ ∴∠1=∠2 ∴ ?A’C’/AC ??= ??OC’/OC ∴∠ACB=∠A’C’B’ ??B’C’/BC? ?= ??A’C’?? ∴△ABC∽△A’B’C’B A C O B’ C’ A’ 1 3 2 4 或AP:AC=AC:AB3、如图点P是△ABC的AB边上的一点,要使△APC∽△ACB,则需补上哪一个条件?4、如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足怎样关系时, △PCA∽△BDP.
(2)当△PCA∽ △BDP时,求∠APB的度数.PBCDA5.如图,不能判定△ACD∽△ABC的条件是( ) A ∠ACD=∠B B ∠ADC=∠ACB C AC·BC=AB·DC D AC2=AD·AB 4.如图,DE∥BC,则图中一共有( )对相似三角形。 ?????????????????????? C DB A A B C DE(3)(4)C2相似三角形
性质总结相似三角形的性质对应角相等
对应边成比例
对应高
对应中线
对应角平分线
周长比等于相似比
面积比等于相似比的平方的比等于相似比理解1.两个相似三角形的一对对应边分别是35厘米和14 厘米,
(1)它们的周长差60厘米,这两个三角形的周长分别是
——————。
(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是_____________。如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?1.已知梯形ABCD中, AD∥BC,对角线AC、BD交于点O,若△AOD的面积为4cm2, △BOC的面积为9cm2, 则梯形ABCD的面积_________cm2∵AD∥BC25例2、如图,DE∥BC,EF∥AB,且S△ADE=25,S△CEF=36.
求△ABC的面积.解:∵DE∥BC,EF∥AB∴∠A=∠CEF,∠AED=∠C∴△ADE∽△EFC∴∵DE∥BC∴△ADE∽△ABC∵ S△ADE=25∴S △ABC=121∴∴∴相似三角形的
应用2.在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为X米,则答:楼高36米.运用5.小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高AB? BDC运用AE答:塔高30米.解:∵∠DEC=∠ABC=90° ∠DCE=∠ACB
∴△DEC∽△ABC运用 皮皮欲测楼房高度,他借助一长5m的标竿,当楼房顶部、标竿顶端与他的眼睛在一条直线 上时,其他人测出AB=4cm,AC=12m。已知皮皮眼睛离地面1.6m.请你帮他算出楼房的高度。GH41251.67.如图,正方形ABCD的边长为8,E是AB的中点,点M,N分别在BC,CD上,且CM=2,则当CN=_________时,△CMN与△ADE相似。1或4在?ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟?BPQ与?BAC相似?在直角梯形ABCD中,AD=7,AB=2,DC=3 P为AD上一点,以P,D,C为顶点的三角形与以P,A,B为顶点的三角形相似,那么这样的点有几个?DAPBCEABC.2、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2, 在AC上取一点F,使以A、E、F为顶点的三角形与 △ABC相似,那么AF=________2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °, ∠DEF= ° ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.AB=2 BC=2EF=2 DE=例 3 如图矩形ABCD是由三个正方形ABEG,GEFH,HFCD组成的,找出图中的相似三角形.解:△ AEF∽ △CEA.理由是:
设小正方形的边长是1,由勾股定理得∴△ AEF ∽ △CEA.
(三边对应边成比例的两个三角形相似.)∴△ AEF ∽ △CEA.
(两条对应边成比例且它们的夹角对应相等的两个三角形相似.)∵∠ AEF = ∠CEA=135°.
19、如图(6), △ABC中,DE??FG??BC,
AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=_________
答案:1:3:5画一画1、 在方格纸中,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.在如图4×4的格纸中, △ABC是一个格点三角形(1)在右图中,请你画一个格点三角形,使它与△ABC相似(相似比不为1)(2)在右图中,请你再画一个格点三角形,使它与△ABC相似(相似比不为1),但与图1中所画的三角形大小不一样.例5、如图, AB/AD=BC/DE=AC/AE.
(1) 求证: ∠BAD= ∠CAE;
(2) 若已知 AB=6, BD=3, AC=4, 求 CE 的长.(1) ∵ 得∴ΔABC∽ΔADE ∴ ∠BAC=∠DAE∴ ∠BAC-∠DAC=∠DAE-∠DAC 即∠BAD=∠CAE(2) 由∴∵∠BAD=∠CAE ∴ΔABD∽ΔACE∴∴ 证明:相似与函数的相关习题
预备定理定理:平行于三角形一边的直线和其他两边相交 (或两边的延长线相交 ) 所构成的三角形与原三角形相似.数学语言: 在△ADE与△ABC中∵DE∥BC ∴△ADE∽△ABC“A”型 “X”型 1、如图,E是 ABCD的边BC的延长线
上的一点,连接AE交CD于F,则图中共有相
似三角形:( )
A.1对 B.2对 C.3对 D.4对小试牛刀 △ADF∽ △ECF △EBA∽ △ECF △ADF∽ △EBA 2.在△ABC中,DE∥BC, 若AD:DB=1:3,DE=2 求BC的长?
3. 如图,△ABC中,AB=8,AC=6,BC=9,如果动点D以每秒2个单位长的速度,从点B出发沿AB方向向点A运动,直线DE//BE,记x秒时这条直线在△ABC内部的长度为y,写出y关于x的函数关系式,解:∵DE//BC∴△ADE∽△ABC又AD=8-2x(0≤x≤4)相似三角形的
判定AACC'∵ ∠A=∠A', ∠B=∠B'∴ ΔABC ∽ ΔA'B'C'用数学符号表示:判定定理3:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角对应相等,两三角形相似。1、判断题:
⑴ 所有的直角三角形都相似 . ( )
⑵ 所有的等边三角形都相似. ( )
⑶ 所有的等腰直角三角形都相似. ( )
⑷ 有一个角相等的两等腰三角形相似 . ( )
×√√×基础演练2、求证:直角三角形被斜边上的高分成的两个直角三角形和原三角形相似。已知:在RtΔABC中,CD是斜边AB上的高。证明: ∵ ∠A=∠A,∠ADC=∠ACB=900,此结论可以称为:“射影定理”,又叫“母子相似定理”∴ ΔACD∽ΔABC(两角对应相等,两 三角形相似)。同理 ΔCBD ∽ ΔABC 。∴ ΔABC∽ΔCBD∽ΔACD。求证:(2)AC2=AD · AB (3) CD2=AD · DB
可得(1) BC2=BD · AB DBC3、如图:在Rt △ ABC中 , ∠ABC=90° BD⊥AC于D
② 求证:AB2=AD · AC BD2=AD · DCA 证明 ∵ ∠ABC=900,BD⊥AC
∴ △ ADB ∽ △ ABC
∴AB∶AC=AD∶AB
∴AB2=AD · AC
∵ ∠ABC=900,BD⊥AC
∴ △ ADB ∽ △ CDB
∴ AD∶BD=BD∶DC
∴ BD2=AD · DC
4、如图所示, 锐角△ ABC 的高CD和BE相交于点O,图中与△ ODB相似的三角形的个数有( )
A 1 B 2 C 3 D 45、如图所示,∠ 1= ∠ 2= ∠ 3,∠ C= ∠ E, △ABC 和 △ ADE相似吗?请说明理由。解: △ ABC ∽ △ADE .理由 :
ABCDE 123 ∵ ∠ 1= ∠ 2= ∠ 3,即∠BAC= ∠DAE又∵ ∠ C= ∠ E, ∠ △ ABC ∽ △ADE ∴∠ 1+ ∠ 2= ∠ 2+ ∠ 3,ABCDECOSSS1. 如图,判断两个三角形是否相似,∴△ABC∽△DFC.解:运用2试说明∠BAD=∠CAE.∴ΔABC∽ΔADE
∴∠BAC=∠DAE
∴∠BAC━∠DAC=∠DAE━∠DAC
即∠BAD=∠CAESAS如图:∠DAB=∠CAE且AC×AD=AE×AB
找出与∠ADE相等的角DECBA如图: AB∥CD 求 证:OA·OD=OB·OCABDCO理解4:2=5:x=6:y
4:x=5:2=6:y
4:x=5:y=6:2要作两个形状相同的三角形框架,其中一个三角形的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?这个问题有其他答案吗?4562延伸练习1、已知:如图,在ΔABC中,AD、BE分别是
BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;F答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.2、如图,已知BC∥B'C',AC∥A'C' 求证:△ABC∽△A'B'C' ???????????????????????????? 证明:∵BC∥B’C’ ∴∠3=∠4, B’C’/BC ??= OC’/OC
∵AC∥A’C’ ∴∠1=∠2 ∴ ?A’C’/AC ??= ??OC’/OC ∴∠ACB=∠A’C’B’ ??B’C’/BC? ?= ??A’C’?? ∴△ABC∽△A’B’C’B A C O B’ C’ A’ 1 3 2 4 或AP:AC=AC:AB3、如图点P是△ABC的AB边上的一点,要使△APC∽△ACB,则需补上哪一个条件?4、如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足怎样关系时, △PCA∽△BDP.
(2)当△PCA∽ △BDP时,求∠APB的度数.PBCDA5.如图,不能判定△ACD∽△ABC的条件是( ) A ∠ACD=∠B B ∠ADC=∠ACB C AC·BC=AB·DC D AC2=AD·AB 4.如图,DE∥BC,则图中一共有( )对相似三角形。 ?????????????????????? C DB A A B C DE(3)(4)C2相似三角形
性质总结相似三角形的性质对应角相等
对应边成比例
对应高
对应中线
对应角平分线
周长比等于相似比
面积比等于相似比的平方的比等于相似比理解1.两个相似三角形的一对对应边分别是35厘米和14 厘米,
(1)它们的周长差60厘米,这两个三角形的周长分别是
——————。
(2)它们的面积之和是58平方厘米,这两个三角形的面积分别是_____________。如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以如图,这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?1.已知梯形ABCD中, AD∥BC,对角线AC、BD交于点O,若△AOD的面积为4cm2, △BOC的面积为9cm2, 则梯形ABCD的面积_________cm2∵AD∥BC25例2、如图,DE∥BC,EF∥AB,且S△ADE=25,S△CEF=36.
求△ABC的面积.解:∵DE∥BC,EF∥AB∴∠A=∠CEF,∠AED=∠C∴△ADE∽△EFC∴∵DE∥BC∴△ADE∽△ABC∵ S△ADE=25∴S △ABC=121∴∴∴相似三角形的
应用2.在同一时刻物体的高度与它的影长成正比例,在某一时刻,有人测得一高为1.8米的竹竿的影长为3米,某一高楼的影长为60米,那么高楼的高度是多少米?解:设高楼的高度为X米,则答:楼高36米.运用5.小明要测量一座古塔的高度,从距他2米的一小块积水处C看到塔顶的倒影,已知小明的眼部离地面的高度DE是1.5米,塔底中心B到积水处C的距离是40米.求塔高AB? BDC运用AE答:塔高30米.解:∵∠DEC=∠ABC=90° ∠DCE=∠ACB
∴△DEC∽△ABC运用 皮皮欲测楼房高度,他借助一长5m的标竿,当楼房顶部、标竿顶端与他的眼睛在一条直线 上时,其他人测出AB=4cm,AC=12m。已知皮皮眼睛离地面1.6m.请你帮他算出楼房的高度。GH41251.67.如图,正方形ABCD的边长为8,E是AB的中点,点M,N分别在BC,CD上,且CM=2,则当CN=_________时,△CMN与△ADE相似。1或4在?ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟?BPQ与?BAC相似?在直角梯形ABCD中,AD=7,AB=2,DC=3 P为AD上一点,以P,D,C为顶点的三角形与以P,A,B为顶点的三角形相似,那么这样的点有几个?DAPBCEABC.2、如图, 在△ABC中,AB=5,AC=4,E是AB上一点,AE=2, 在AC上取一点F,使以A、E、F为顶点的三角形与 △ABC相似,那么AF=________2.如图,在4×4的正方形方格中,△ABC和△DEF
的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC= °, ∠DEF= ° ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.AB=2 BC=2EF=2 DE=例 3 如图矩形ABCD是由三个正方形ABEG,GEFH,HFCD组成的,找出图中的相似三角形.解:△ AEF∽ △CEA.理由是:
设小正方形的边长是1,由勾股定理得∴△ AEF ∽ △CEA.
(三边对应边成比例的两个三角形相似.)∴△ AEF ∽ △CEA.
(两条对应边成比例且它们的夹角对应相等的两个三角形相似.)∵∠ AEF = ∠CEA=135°.
19、如图(6), △ABC中,DE??FG??BC,
AD=DF=FB,则S△ADE:S四边形DFGE:S四边形FBCG=_________
答案:1:3:5画一画1、 在方格纸中,每个小格的顶点叫做格点,以格点为顶点的三角形叫做格点三角形.在如图4×4的格纸中, △ABC是一个格点三角形(1)在右图中,请你画一个格点三角形,使它与△ABC相似(相似比不为1)(2)在右图中,请你再画一个格点三角形,使它与△ABC相似(相似比不为1),但与图1中所画的三角形大小不一样.例5、如图, AB/AD=BC/DE=AC/AE.
(1) 求证: ∠BAD= ∠CAE;
(2) 若已知 AB=6, BD=3, AC=4, 求 CE 的长.(1) ∵ 得∴ΔABC∽ΔADE ∴ ∠BAC=∠DAE∴ ∠BAC-∠DAC=∠DAE-∠DAC 即∠BAD=∠CAE(2) 由∴∵∠BAD=∠CAE ∴ΔABD∽ΔACE∴∴ 证明:相似与函数的相关习题
