13.3.2 等腰三角形的判定 同步练习(解析版)
文档属性
| 名称 | 13.3.2 等腰三角形的判定 同步练习(解析版) | 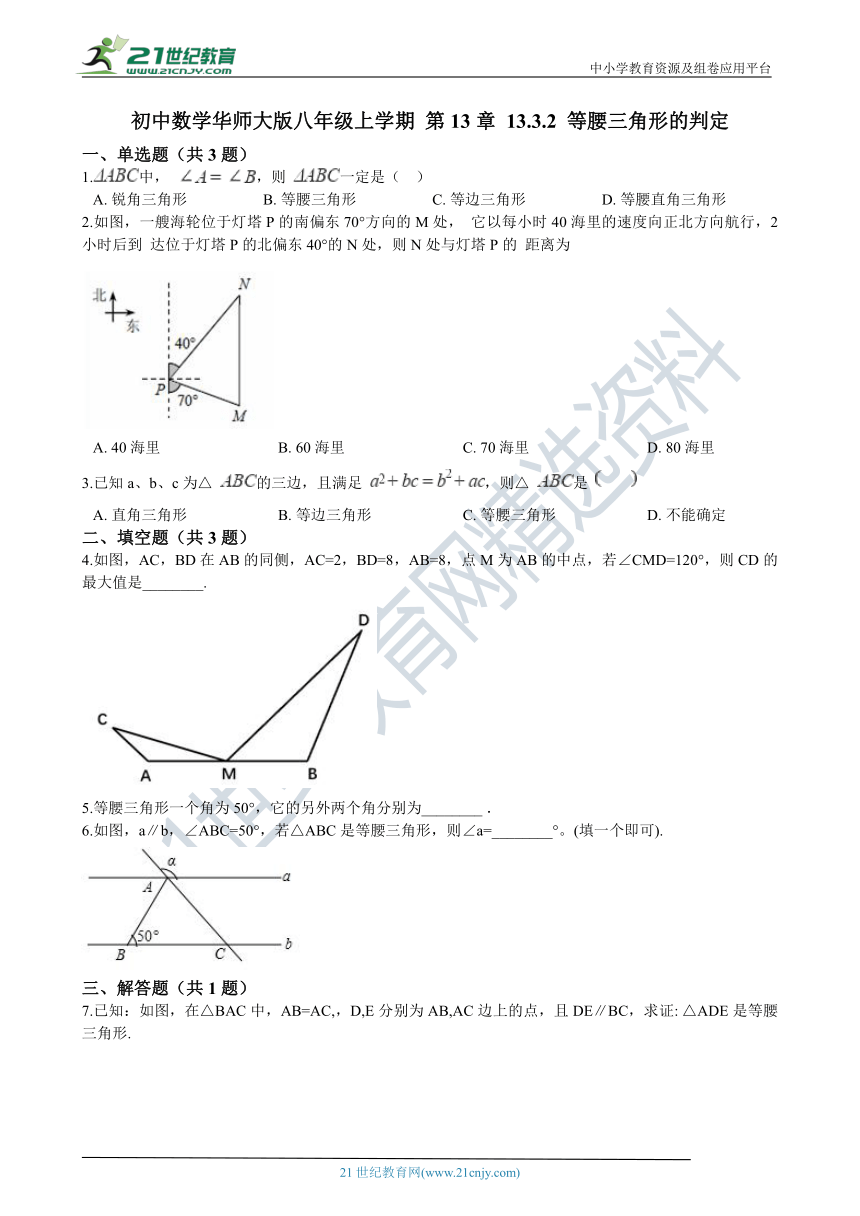 | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-30 09:22:56 | ||
图片预览



文档简介
初中数学华师大版八年级上学期 第13章 13.3.2 等腰三角形的判定
一、单选题(共3题)
1.中, ,则 一定是(?? )
A.?锐角三角形????????????????????B.?等腰三角形????????????????????C.?等边三角形????????????????????D.?等腰直角三角形
2.如图,一艘海轮位于灯塔P的南偏东70°方向的M处, 它以每小时40海里的速度向正北方向航行,2小时后到 达位于灯塔P的北偏东40°的N处,则N处与灯塔P的 距离为 【来源:21·世纪·教育·网】
A.?40海里???????????????????????????????B.?60海里???????????????????????????????C.?70海里???????????????????????????????D.?80海里
3.已知a、b、c为△ 的三边,且满足 ,则△ 是 ? ???
A.?直角三角形????????????????????????B.?等边三角形????????????????????????C.?等腰三角形????????????????????????D.?不能确定
二、填空题(共3题)
4.如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是________. 21·世纪*教育网
5.等腰三角形一个角为50°,它的另外两个角分别为________?.
6.如图,a∥b,∠ABC=50°,若△ABC是等腰三角形,则∠a=________°。(填一个即可).
三、解答题(共1题)
7.已知:如图,在△BAC中,AB=AC,,D,E分别为AB,AC边上的点,且DE∥BC,求证: △ADE是等腰三角形. 2-1-c-n-j-y
四、综合题(共4题)
8.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段AB上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线AC段于E. 21*cnjy*com
(1)当∠BDA=115°时,∠BAD=________°,∠DEC=________°;
(2)当DC等于多少时,△ABD与△DCE全等?请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由. 21世纪教育网版权所有
9.如图,AB⊥EF,DC⊥EF,垂足分别为B、C,且AB=CD,BE=CF.AF、DE相交于点O,AF、DC相交于点N,DE、AB相交于点M. 2·1·c·n·j·y
(1)请直接写出图中所有的等腰三角形;
(2)求证:△ABF≌△DCE.
10.在△ABC中,AC=5,BC=2,且AB长为奇数.
(1)求△ABC的周长;
(2)判定△ABC的形状.
11.如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
答案解析部分
一、单选题
1. B
解:根据在三角形中“等角对等边”,可知,选项B符合题意. 【分析】根据两角相等的三角形是等腰三角形判断即可.21教育网
2. D
解:依题意,知MN=40海里/小时×2小时=80海里,
∵根据方向角的意义和平行的性质,∠M=70°,∠N=40°,
∴根据三角形内角和定理得∠MPN=70°。∴∠M=∠MPN=70°。
∴NP=NM=80海里。
故答案为:D。 【分析】?先计算出MN的长,再根据方向角的意义平行线的性质求出∠M,∠N的度数,然后根据三角形内角和求出∠NPM的度数,可得∠M=∠MPN,最后根据等腰三角形的判定求得NP=NM即可得出答案
3. C
解:∵a2+bc=b2+ac ∴a2-b2+bc-ac=(a+b)(a-b)+c(a-b)=0 ∴(a-b)(a-b+c)=0 ∵a-b+c>0,即a-b+c≠0 ∴a-b=0即a=b ∴△ABC是等腰三角形。 【分析】将a2+bc=b2+ac转化为(a-b)(a-b+c)=0,利用三角形三边关系定理,可证得a=b,即可判断得出△ABC的形状。【来源:21cnj*y.co*m】
二、填空题
4. 14
解:作点A,N关于CM对称,作点B、E关于MD对称,连接MN,ME,CN,NE,DE ∵点M为AB的中点,AB=8 ∴AM=BM=4 ∴△ACM≌△CMN ∴AC=CN=2,AM=NM=4,∠AMC=∠CMN???? 同理可证:BD=DE=8,BM=ME=4,∠BMD=∠EMD ∵∠CMD=120° ∴∠AMC+∠BMD=180°-120°=60° ∴∠CMN+∠EMD=60° ∴∠NME=180°-60°-60°=60° ∴△MNE是等边三角形 ∴NE=ME=4 ∵CD≤CE+NE+DE ∴当点C、N、E、D共线时,CD的值最大 ∴CD的最大值为CE+NE+DE=2+4+8=14 【分析】 作点A,N关于CM对称,作点B、E关于MD对称,连接MN,ME,CN,NE,DE,利用轴对称的性质易证AC=CN=2,AM=NM=4,∠AMC=∠CMN? ,BD=DE=8,BM=ME=4,∠BMD=∠EMD,再由∠CMD=120°,去证明∠NME=60°,就可得到△MNE是等边三角形,求出NE的长,再由CD≤CE+NE+DE,可知当点C、N、E、D共线时,CD的值最大,然后就可求出CD的最大值。【出处:21教育名师】
5. 略
解:当该角为等腰三角形的顶角时,另外两个角分别为65°,65°;当该角为等腰三角形的底角时,两外两个角的为50°,80°。 【版权所有:21教育】
【分析】根据等腰三角形的性质分别进行判断即可得到答案。
6. 130(答案不唯一)
解: 如图 △ABC是等腰三角形 当∠ABC=∠ACB时, ∵∠ABC=50° ∴∠ACB=50° ∴∠BAC=180°-50°-50°=80° ∵a∥b ∠DAB=∠ABC=50° ∵∠a=∠DAB+∠BAC=50°+80°=130°; 当∠ABC=∠BAC=50°时 ∴∠a=∠DAB+∠BAC=50°+50°=100°; 当∠BAC=∠ACB时 ∠BAC= ∴∠a=∠DAB+∠BAC=50°+65°=115°; 故答案为:130°或100°或115° 21教育名师原创作品
【分析】利用平行线的性质,可求出∠DAB的度数,再利用等腰三角形的定义,分情况讨论:当∠ABC=∠ACB时;当∠ABC=∠BAC=50°时;当∠BAC=∠ACB时,再由∠a=∠DAB+∠BAC,可求解。
三、解答题
7. 证明:∵AB=AC,
∴∠B=∠C,
又∵DE∥BC,
∴∠B=∠ADE,∠C=∠AED,
∴∠ADE=∠AED,
∴AD=AE,
∴△ADE是等腰三角形.
【分析】根据等边对等角得出 ∠B=∠C, 根据二直线平行,同位角相等得出 ∠B=∠ADE,∠C=∠AED, 故 ∠ADE=∠AED, 根据等角对等边得出 AD=AE, 从而得出结论.
四、综合题
8. (1)25 ;115 (2)解: 当DC=2时,△ABD≌△DCE, 理由如下: ∵∠C=40°, ∴∠DEC+∠EDC=180°-∠C=140°, ∵∠ADE=40°, ∴∠ADB+∠EDC=140°, ∴∠ADB=∠DEC, ∵AB=AC=2 ∴AB=DC=2, 在△ABD和△DCE中, ∴△ABD≌△DCE(AAS) ∴当DC=2时,△ABD≌△DCE. (3)可以; 理由:当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形, ∵当∠BDA=110°时, ∴∠ADC=70°, ∵∠C=40°, ∴∠DAE=70°, ∴∠AED=180°?70°?40°=70° ∴△ADE的形状是等腰三角形; ∵当∠BDA的度数为80°时, ∴∠ADC=180°-∠BDA=100°, ∵∠C=40°, ∴∠DAE=180°-∠ADC-∠C=180°-100°-40°=40°, ∴∠DAE=∠ADE ∴△ADE的形状是等腰三角形. 21*cnjy*com
【分析】(1)在△ABD中,利用三角形内角和定理求出∠BAD的度数;再利用平角的定义求出∠EDC的度数,然后利用三角形的内角和定理可求出∠DEC的度数. (2)利用三角形内角和定理可证得∠DEC+∠EDC=140°,利用平角的定义可证得∠ADB+∠EDC=140°,就可推出∠ADB=∠DEC,当DC=2时,可证AB=DC,因此利用AAS可证得△ABD≌△DCE. (3)分情况讨论:当∠BDA=110°时;当∠BDA的度数为80°时,分别利用三角形的内角和定理及等腰三角形的判断方法,可证得结论.
9. (1)解:△EOF,△AOM,△DON (2)证明:∵AB⊥EF于点B,DC⊥EF于点C, 21cnjy.com
∴∠ABC=∠DCB=90°,
∵CF=BE,
∴CF+BC=BE+BC,
即BF=CE…
在△ABF和△DCE中,
,
∴△ABF≌△DCE,
【分析】(1)首先利用SAS判断出△ABF≌△DCE,根据全等三角形对应角相等可得∠A=∠D,∠DEC=∠AFB,所以△EOF是等腰三角形,再根据等角的余角相等可得∠A=∠AMO,∠D=∠DNO,从而得到△AOM与△DON也都是等腰三角形; (2)根据等式的性质,由BE=CF,得出EC=BF,然后利用SAS判断出△ABF≌△DCE。 ?www.21-cn-jy.com
10. (1)解:由题意得:5﹣2<AB<5+2,
即:3<AB<7,
∵AB为奇数,
∴AB=5,
∴△ABC的周长为5+5+2=12
(2)解:∵AB=AC=5,
∴△ABC是等腰三角形.
【分析】(1)利用三角形三边关系定理求出AB的取值范围,再根据AB长为奇数,确定出AB的值,然后求出△ABC的周长。 (2)由(1)可知AB=AC,即可判定出△ABC的形状。www-2-1-cnjy-com
11. (1)解:△BDE是等腰三角形.
由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
即△BDE是等腰三角形
(2)解:设DE=x,则BE=x,AE=8﹣x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即42+(8﹣x)2=x2 ,
解得:x=5,
所以S△BDE= DE×AB= ×5×4=10.
【分析】(1)利用折叠的性质,可知∠CBD=∠EBD,再利用矩形的性质及平行线的性质,可证得∠CBD=∠EDB,从而可推出∠EBD=∠EDB,然后利用等角对等边,可证得结论。 (2)设DE=x,用含x的代数式表示出BE,AE的长,在Rt△ABE中,利用勾股定理建立关于x的方程,解方程求出x的值,就可得到DE的长,然后利用三角形的面积公式可求解。21·cn·jy·com
一、单选题(共3题)
1.中, ,则 一定是(?? )
A.?锐角三角形????????????????????B.?等腰三角形????????????????????C.?等边三角形????????????????????D.?等腰直角三角形
2.如图,一艘海轮位于灯塔P的南偏东70°方向的M处, 它以每小时40海里的速度向正北方向航行,2小时后到 达位于灯塔P的北偏东40°的N处,则N处与灯塔P的 距离为 【来源:21·世纪·教育·网】
A.?40海里???????????????????????????????B.?60海里???????????????????????????????C.?70海里???????????????????????????????D.?80海里
3.已知a、b、c为△ 的三边,且满足 ,则△ 是 ? ???
A.?直角三角形????????????????????????B.?等边三角形????????????????????????C.?等腰三角形????????????????????????D.?不能确定
二、填空题(共3题)
4.如图,AC,BD在AB的同侧,AC=2,BD=8,AB=8,点M为AB的中点,若∠CMD=120°,则CD的最大值是________. 21·世纪*教育网
5.等腰三角形一个角为50°,它的另外两个角分别为________?.
6.如图,a∥b,∠ABC=50°,若△ABC是等腰三角形,则∠a=________°。(填一个即可).
三、解答题(共1题)
7.已知:如图,在△BAC中,AB=AC,,D,E分别为AB,AC边上的点,且DE∥BC,求证: △ADE是等腰三角形. 2-1-c-n-j-y
四、综合题(共4题)
8.如图,在△ABC中,AB=AC=2,∠B=40°,点D在线段AB上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线AC段于E. 21*cnjy*com
(1)当∠BDA=115°时,∠BAD=________°,∠DEC=________°;
(2)当DC等于多少时,△ABD与△DCE全等?请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由. 21世纪教育网版权所有
9.如图,AB⊥EF,DC⊥EF,垂足分别为B、C,且AB=CD,BE=CF.AF、DE相交于点O,AF、DC相交于点N,DE、AB相交于点M. 2·1·c·n·j·y
(1)请直接写出图中所有的等腰三角形;
(2)求证:△ABF≌△DCE.
10.在△ABC中,AC=5,BC=2,且AB长为奇数.
(1)求△ABC的周长;
(2)判定△ABC的形状.
11.如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
答案解析部分
一、单选题
1. B
解:根据在三角形中“等角对等边”,可知,选项B符合题意. 【分析】根据两角相等的三角形是等腰三角形判断即可.21教育网
2. D
解:依题意,知MN=40海里/小时×2小时=80海里,
∵根据方向角的意义和平行的性质,∠M=70°,∠N=40°,
∴根据三角形内角和定理得∠MPN=70°。∴∠M=∠MPN=70°。
∴NP=NM=80海里。
故答案为:D。 【分析】?先计算出MN的长,再根据方向角的意义平行线的性质求出∠M,∠N的度数,然后根据三角形内角和求出∠NPM的度数,可得∠M=∠MPN,最后根据等腰三角形的判定求得NP=NM即可得出答案
3. C
解:∵a2+bc=b2+ac ∴a2-b2+bc-ac=(a+b)(a-b)+c(a-b)=0 ∴(a-b)(a-b+c)=0 ∵a-b+c>0,即a-b+c≠0 ∴a-b=0即a=b ∴△ABC是等腰三角形。 【分析】将a2+bc=b2+ac转化为(a-b)(a-b+c)=0,利用三角形三边关系定理,可证得a=b,即可判断得出△ABC的形状。【来源:21cnj*y.co*m】
二、填空题
4. 14
解:作点A,N关于CM对称,作点B、E关于MD对称,连接MN,ME,CN,NE,DE ∵点M为AB的中点,AB=8 ∴AM=BM=4 ∴△ACM≌△CMN ∴AC=CN=2,AM=NM=4,∠AMC=∠CMN???? 同理可证:BD=DE=8,BM=ME=4,∠BMD=∠EMD ∵∠CMD=120° ∴∠AMC+∠BMD=180°-120°=60° ∴∠CMN+∠EMD=60° ∴∠NME=180°-60°-60°=60° ∴△MNE是等边三角形 ∴NE=ME=4 ∵CD≤CE+NE+DE ∴当点C、N、E、D共线时,CD的值最大 ∴CD的最大值为CE+NE+DE=2+4+8=14 【分析】 作点A,N关于CM对称,作点B、E关于MD对称,连接MN,ME,CN,NE,DE,利用轴对称的性质易证AC=CN=2,AM=NM=4,∠AMC=∠CMN? ,BD=DE=8,BM=ME=4,∠BMD=∠EMD,再由∠CMD=120°,去证明∠NME=60°,就可得到△MNE是等边三角形,求出NE的长,再由CD≤CE+NE+DE,可知当点C、N、E、D共线时,CD的值最大,然后就可求出CD的最大值。【出处:21教育名师】
5. 略
解:当该角为等腰三角形的顶角时,另外两个角分别为65°,65°;当该角为等腰三角形的底角时,两外两个角的为50°,80°。 【版权所有:21教育】
【分析】根据等腰三角形的性质分别进行判断即可得到答案。
6. 130(答案不唯一)
解: 如图 △ABC是等腰三角形 当∠ABC=∠ACB时, ∵∠ABC=50° ∴∠ACB=50° ∴∠BAC=180°-50°-50°=80° ∵a∥b ∠DAB=∠ABC=50° ∵∠a=∠DAB+∠BAC=50°+80°=130°; 当∠ABC=∠BAC=50°时 ∴∠a=∠DAB+∠BAC=50°+50°=100°; 当∠BAC=∠ACB时 ∠BAC= ∴∠a=∠DAB+∠BAC=50°+65°=115°; 故答案为:130°或100°或115° 21教育名师原创作品
【分析】利用平行线的性质,可求出∠DAB的度数,再利用等腰三角形的定义,分情况讨论:当∠ABC=∠ACB时;当∠ABC=∠BAC=50°时;当∠BAC=∠ACB时,再由∠a=∠DAB+∠BAC,可求解。
三、解答题
7. 证明:∵AB=AC,
∴∠B=∠C,
又∵DE∥BC,
∴∠B=∠ADE,∠C=∠AED,
∴∠ADE=∠AED,
∴AD=AE,
∴△ADE是等腰三角形.
【分析】根据等边对等角得出 ∠B=∠C, 根据二直线平行,同位角相等得出 ∠B=∠ADE,∠C=∠AED, 故 ∠ADE=∠AED, 根据等角对等边得出 AD=AE, 从而得出结论.
四、综合题
8. (1)25 ;115 (2)解: 当DC=2时,△ABD≌△DCE, 理由如下: ∵∠C=40°, ∴∠DEC+∠EDC=180°-∠C=140°, ∵∠ADE=40°, ∴∠ADB+∠EDC=140°, ∴∠ADB=∠DEC, ∵AB=AC=2 ∴AB=DC=2, 在△ABD和△DCE中, ∴△ABD≌△DCE(AAS) ∴当DC=2时,△ABD≌△DCE. (3)可以; 理由:当∠BDA的度数为110°或80°时,△ADE的形状是等腰三角形, ∵当∠BDA=110°时, ∴∠ADC=70°, ∵∠C=40°, ∴∠DAE=70°, ∴∠AED=180°?70°?40°=70° ∴△ADE的形状是等腰三角形; ∵当∠BDA的度数为80°时, ∴∠ADC=180°-∠BDA=100°, ∵∠C=40°, ∴∠DAE=180°-∠ADC-∠C=180°-100°-40°=40°, ∴∠DAE=∠ADE ∴△ADE的形状是等腰三角形. 21*cnjy*com
【分析】(1)在△ABD中,利用三角形内角和定理求出∠BAD的度数;再利用平角的定义求出∠EDC的度数,然后利用三角形的内角和定理可求出∠DEC的度数. (2)利用三角形内角和定理可证得∠DEC+∠EDC=140°,利用平角的定义可证得∠ADB+∠EDC=140°,就可推出∠ADB=∠DEC,当DC=2时,可证AB=DC,因此利用AAS可证得△ABD≌△DCE. (3)分情况讨论:当∠BDA=110°时;当∠BDA的度数为80°时,分别利用三角形的内角和定理及等腰三角形的判断方法,可证得结论.
9. (1)解:△EOF,△AOM,△DON (2)证明:∵AB⊥EF于点B,DC⊥EF于点C, 21cnjy.com
∴∠ABC=∠DCB=90°,
∵CF=BE,
∴CF+BC=BE+BC,
即BF=CE…
在△ABF和△DCE中,
,
∴△ABF≌△DCE,
【分析】(1)首先利用SAS判断出△ABF≌△DCE,根据全等三角形对应角相等可得∠A=∠D,∠DEC=∠AFB,所以△EOF是等腰三角形,再根据等角的余角相等可得∠A=∠AMO,∠D=∠DNO,从而得到△AOM与△DON也都是等腰三角形; (2)根据等式的性质,由BE=CF,得出EC=BF,然后利用SAS判断出△ABF≌△DCE。 ?www.21-cn-jy.com
10. (1)解:由题意得:5﹣2<AB<5+2,
即:3<AB<7,
∵AB为奇数,
∴AB=5,
∴△ABC的周长为5+5+2=12
(2)解:∵AB=AC=5,
∴△ABC是等腰三角形.
【分析】(1)利用三角形三边关系定理求出AB的取值范围,再根据AB长为奇数,确定出AB的值,然后求出△ABC的周长。 (2)由(1)可知AB=AC,即可判定出△ABC的形状。www-2-1-cnjy-com
11. (1)解:△BDE是等腰三角形.
由折叠可知,∠CBD=∠EBD,
∵AD∥BC,
∴∠CBD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
即△BDE是等腰三角形
(2)解:设DE=x,则BE=x,AE=8﹣x,
在Rt△ABE中,由勾股定理得:AB2+AE2=BE2即42+(8﹣x)2=x2 ,
解得:x=5,
所以S△BDE= DE×AB= ×5×4=10.
【分析】(1)利用折叠的性质,可知∠CBD=∠EBD,再利用矩形的性质及平行线的性质,可证得∠CBD=∠EDB,从而可推出∠EBD=∠EDB,然后利用等角对等边,可证得结论。 (2)设DE=x,用含x的代数式表示出BE,AE的长,在Rt△ABE中,利用勾股定理建立关于x的方程,解方程求出x的值,就可得到DE的长,然后利用三角形的面积公式可求解。21·cn·jy·com
