13.2.3 边角边 同步练习(解析版)
文档属性
| 名称 | 13.2.3 边角边 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-30 09:39:42 | ||
图片预览



文档简介
初中数学华师大版八年级上学期 第13章 13.2.3 边角边
一、单选题(共2题)
1.下面各条件中,能使△ABC≌△DEF的条件是(????? )
A.?AB=DE,∠A=∠D,BC=EF B.?AB=BC,∠B=∠E,DE=EF C.?AB=EF,∠A=∠D,AC=DF D.?BC=EF,∠C=∠F,AC=DF21教育网
2.如图,已知 ,添加条件后,可得 ,则在下列条件中,不能添加的是(???? )
A.????????????????????B.????????????????????C.????????????????????D.?
二、填空题(共4题)
3.如图点C,D在AB同侧,AD=BC,添加一个条件________就能使△ABD≌△BAC。
4.如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且 ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;② 的周长为 ;③ ;④ 的面积的最大值 .其中正确的结论是________.(填写所有正确结论的序号) 21·cn·jy·com
5.如图,点B,A,D,E在同一直线上,BD=AE,BC∥EF,要使△ABC △DEF,则只需添加一个适当的条件是________(只填一个即可) 2·1·c·n·j·y
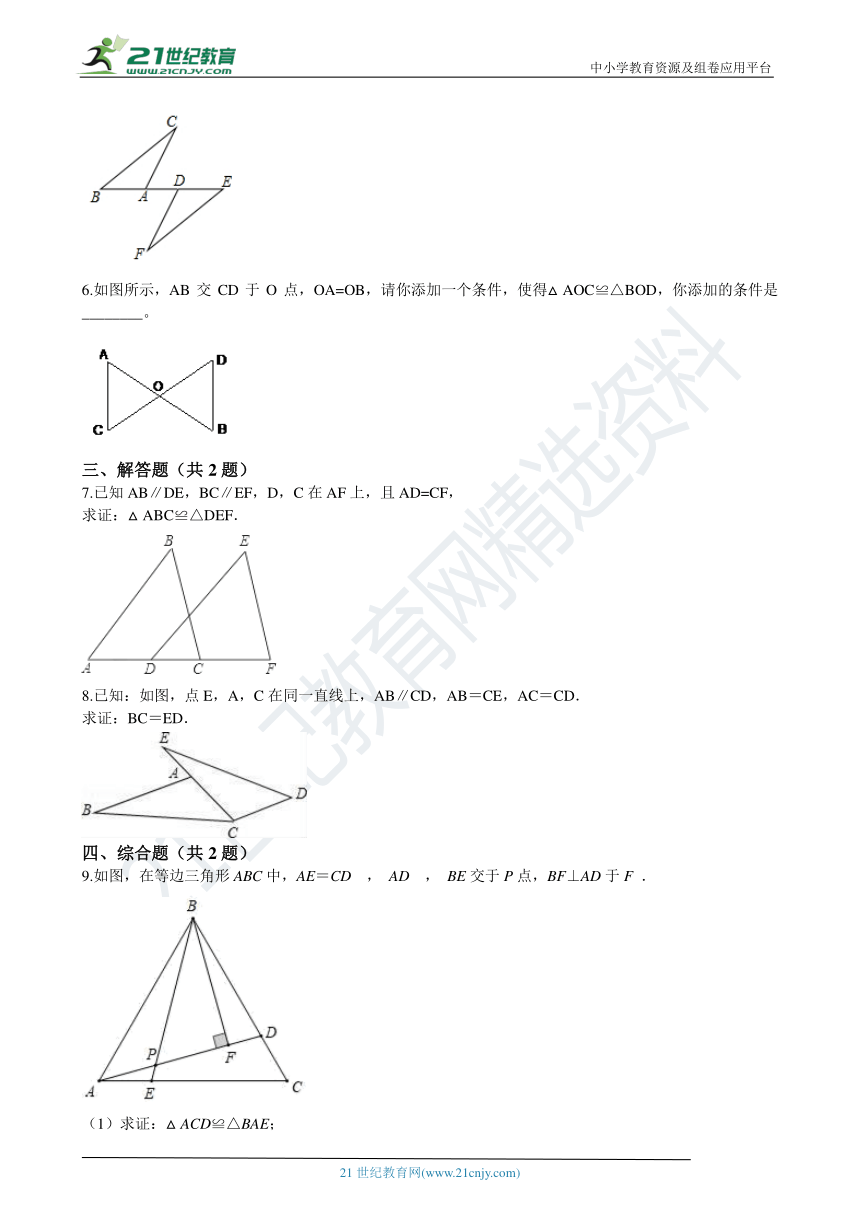
6.如图所示,AB交CD于O点,OA=OB,请你添加一个条件,使得△AOC≌△BOD,你添加的条件是________。
三、解答题(共2题)
7.已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,
求证:△ABC≌△DEF.
8.已知:如图,点E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD.
求证:BC=ED.
四、综合题(共2题)
9.如图,在等边三角形ABC中,AE=CD , AD , BE交于P点,BF⊥AD于F .
(1)求证:△ACD≌△BAE;
(2)求证:BF= PF .
10.如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF. 21·世纪*教育网
(1)DF=________;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
答案解析部分
一、单选题
1. D
解:∵AB=DE,BC=EF ,∠A=∠D,两边及一边的对角对应相等, ∴△ABC和△DEF不一定全等,故A不符合题意; ∵AB=BC,∠B=∠E,DE=EF,这两个三角形中只有一组对应角相等, ∴△ABC和△DEF不一定全等,故B不符合题意; ∵ AB=EF,∠A=∠D,AC=DF ,EF和DF的夹角为∠F, ∴△ABC和△DEF不全等,故C不符合题意; ∵ BC=EF,∠C=∠F,AC=DF ∴△ABC≌△DEF(SAS),故D符合题意; 故答案为:D 【分析】利用判定两三角形全等的方法:SSS,SAS,AAS,ASA,对各选项逐一判断,即可得出答案:注意对应边和对应角。2-1-c-n-j-y
2. D
解:A、∵∠BAD=∠CAD,
∴ ,
∴△ABD≌△ACD(ASA);故不符合题意;
B、∵∠B=∠C,
∴??? ,
∴△ABD≌△ACD(AAS);故不符合题意;
C、∵BD=CD,
∴ ,
∴△ABD≌△ACD(SAS);故不符合题意;
D、AB=AC与∠ADB=∠ADC、AD=AD组成了SSA不能由此判定三角形全等,故符合题意。
故答案为:D。
【分析】根据题干及图形提供的条件来看,已经具有AD=AD, ,要使 只需要再添加任意一对角对应相等或BD=CD即可,从而即可一一判断得出答案。
二、填空题
3. ∠DAB=∠CBA或AC=BD
解:∵在△ABD和△BAC中, ∴△ABD≌△BAC(SAS),故可以添加∠DAB=∠CBA; 在△ABD和△BAC中, ∴△ABD≌△BAC(SAS),故可以添加AC=BD; 故答案为:∠DAB=∠CBA或AC=BD 【分析】观察图形,隐含条件为:AB=BA,因此利用SAS,可以添加∠DAB=∠CBA,利用SSS可以添加AC=BD.21世纪教育网版权所有
4. ①④
解:如图1,在BC上截取BH=BE,连接EH.
?
∵BE=BH,∠EBH=90°,
∴EH= BE,∵AF= BE,∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°,
∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,
∴AE=HC,∴△FAE≌△EHC(SAS),
∴EF=EC,∠AEF=∠ECH,
∵∠ECH+∠CEB=90°,∴∠AEF+∠CEB=90°,∴∠FEC=90°,
∴∠ECF=∠EFC=45°,故①正确,
如图2中,延长AD到H,使得DH=BE,则△CBE≌△CDH(SAS),
∴∠ECB=∠DCH,∴∠ECH=∠BCD=90°,∴∠ECG=∠GCH=45°,
∵CG=CG,CE=CH,∴△GCE≌△GCH(SAS),∴EG=GH,
∵GH=DG+DH,DH=BE,
∴EG=BE+DG,故③错误,
∴△AEG的周长=AE+EG+AG=AG+GH=AD+DH+AE=AE+EB+AD=AB+AD=2a,故②错误,
设BE=x,则AE=a-x,AF= ,
∴∴ ,
∴当 时, 的面积有最大值,最大值是 ,④正确;
故答案为:①④. 【分析】根据全等三角形的判定定理(AAS)和三角形的周长、面积公式,可列出关系式,得到正确的结论。21cnjy.com
5. BC=EF或∠BAC=∠EDF(答案不唯一)
解:∵ BC∥EF ∴∠B=∠E ∵BD=AE ∴ BD-AD=AE-AD,即BA=DE ∴添加BC=EF ∴△ABC≌△DEF(SAS) 添加 ∠BAC=∠EDF ∴△ABC≌△DEF(ASA) 添加∠C=∠F ∴△ABC≌△DEF(AAS) 故答案为: BC=EF或∠BAC=∠EDF或∠C=∠F www-2-1-cnjy-com
【分析】利用平行线的性质,易证∠B=∠E,再由BD=AE,再根据SAS或ASA或AAS添加条件即可得到△ABC≌△DEF。21*cnjy*com
6. OC=OD
理由是:在△AOC和△BOD中,
?
∴△AOC≌△BOD(SAS).
故答案为:OC=OD. 【分析】开放性的命题,答案不唯一,题干中已经具有 OA=OB ,图形中又具有∠AOC=∠BOD,故只要添加任意一组角对应相等,或边OC=OD即可利用三角形全等的判定方法判断出△AOC≌△BOD。
三、解答题
7. 解:∵AB∥DE,BC∥EF, ∴∠A=∠EDF,∠ACB=∠F, ∵AD=CF, ∴AD+DC=CF+CD即AC=DF; 在△ABC和△DEF中, ∴△ABC≌△DEF(SAS) 源【分析】利用平行线的性质,易证∠A=∠EDF,∠ACB=∠F,再利用线段的和差,可证得AC=DF,然后利用SAS可证得结论。【出处:21教育名师】
8. 证明:∵AB∥CD,
∴∠BAC=∠ECD,
在△BAC和△ECD中 ,
∴△BAC≌△ECD(SAS),
∴BC=ED
【分析】根据平行线的性质,即可得到∠BAC=∠ECD,根据边角边的三角形的判定定理即可证明三角形全等,得出BC=ED即可。【版权所有:21教育】
四、综合题
9. (1)证明:如图所示:
∵△ABC是等边三角形,
∴在△ABE和△CAD中,
AB=AC ;
∴△ABE≌△CAD(SAS) (2)证明:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
又∵∠BAE=∠BAP+∠PAE=60°,
∴∠BAP+∠ABP=60°,
又∵∠BPF=∠BAP+∠ABP,
∴∠BPF=60°,
∵BF⊥AD
∴tan∠BPF= ,
∴tan60°= = ,
∴BF= PF
【分析】(1)在等边三角形ABC中,AB=AC,∠BAC=∠C=60°,且AE=CD,根据“两边和其夹角对应相等的两个三角形全等”可证明△ACD≌△BAE; (2)由题(1)可得∠CAD=∠ABE,故∠BPD=∠BAD+∠ABE=∠BAD+∠CAD=60°,由于BF⊥AD,根据三角函数可得tan∠BPF=, 所以可证明BF=PF。www.21-cn-jy.com
10. (1)t (2)证明:∵∠CFD=90°,∠B=90°,
∴DF∥AB,
∴∠AED=∠FDE.
在△AED和△FDE中,AF=FD=t,∠AED=∠FDE,DE=DE,
∴△AED≌△FDE(SAS). (3)∵△AED≌△FDE,
∴当△DEF是等边三角形时,△EDA是等边三角形.
∵∠A=90°﹣∠C=60°,
∴AD=AE.
∵AE=t,AD=AC﹣CD=10﹣2t,
∴t=10﹣2t,
∴t= ,
∴当t为 时,△DEF是等边三角形.
(4)∵△AED≌△FDE,
∴当△DEF为直角三角形时,△EDA是直角三角形.
当∠AED=90°时,AD=2AE,即10﹣2t=2t,
解得:t= ;
当∠ADE=90°时,AE=2AD,即t=2(10﹣2t),
解得:t=4.
综上所述:当t为 或4时,△DEF为直角三角形.
解:(1)∵DF⊥BC,
∴∠CFD=90°.
在Rt△CDF中,∠CFD=90°,∠C=30°,CD=2t,
∴DF= CD=t.
故答案为:t.
【分析】(1)根据30°的角所对的直角边等于斜边的一半可得DF= CD=t.(2)根据两直线平行内错角相等可得 ∠AED=∠FDE,由SAS即可判断△AED≌△FDE ;(3)由 △AED≌△FDE可知, 当△DEF是等边三角形时,△EDA是等边三角形,根据有一个角是60°的等腰三角形是等边三角形可得当 AD=AE,即 t=10﹣2t时, △DEF是等边三角形,解方程求出t值即可.(4)由△AED≌△FDE可知 ,当△DEF为直角三角形时,△EDA是直角三角形. ① 当∠ADE=90°时 ,根据30°的角所对的直角边等于斜边的一半可得 AE=2AD,即t=2(10﹣2t), 解方程求出t值即可.② 当∠AED=90°时,根据30°的角所对的直角边等于斜边的一半可得 AD=2AE,即10﹣2t=2t,解方程求出t值即可.【来源:21·世纪·教育·网】
一、单选题(共2题)
1.下面各条件中,能使△ABC≌△DEF的条件是(????? )
A.?AB=DE,∠A=∠D,BC=EF B.?AB=BC,∠B=∠E,DE=EF C.?AB=EF,∠A=∠D,AC=DF D.?BC=EF,∠C=∠F,AC=DF21教育网
2.如图,已知 ,添加条件后,可得 ,则在下列条件中,不能添加的是(???? )
A.????????????????????B.????????????????????C.????????????????????D.?
二、填空题(共4题)
3.如图点C,D在AB同侧,AD=BC,添加一个条件________就能使△ABD≌△BAC。
4.如图,正方形ABCD的边长为a,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且 ,CF与AD相交于点G,连接EC,EF,EG,则下列结论:①∠ECF=45°;② 的周长为 ;③ ;④ 的面积的最大值 .其中正确的结论是________.(填写所有正确结论的序号) 21·cn·jy·com
5.如图,点B,A,D,E在同一直线上,BD=AE,BC∥EF,要使△ABC △DEF,则只需添加一个适当的条件是________(只填一个即可) 2·1·c·n·j·y
6.如图所示,AB交CD于O点,OA=OB,请你添加一个条件,使得△AOC≌△BOD,你添加的条件是________。
三、解答题(共2题)
7.已知AB∥DE,BC∥EF,D,C在AF上,且AD=CF,
求证:△ABC≌△DEF.
8.已知:如图,点E,A,C在同一直线上,AB∥CD,AB=CE,AC=CD.
求证:BC=ED.
四、综合题(共2题)
9.如图,在等边三角形ABC中,AE=CD , AD , BE交于P点,BF⊥AD于F .
(1)求证:△ACD≌△BAE;
(2)求证:BF= PF .
10.如图,在Rt△ABC中,∠B=90°,AC=10,∠C=30°点D从点C出发沿CA方向以每秒2个单位长度的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长度的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF. 21·世纪*教育网
(1)DF=________;(用含t的代数式表示)
(2)求证:△AED≌△FDE;
(3)当t为何值时,△DEF是等边三角形?说明理由;
(4)当t为何值时,△DEF为直角三角形?(请直接写出t的值.)
答案解析部分
一、单选题
1. D
解:∵AB=DE,BC=EF ,∠A=∠D,两边及一边的对角对应相等, ∴△ABC和△DEF不一定全等,故A不符合题意; ∵AB=BC,∠B=∠E,DE=EF,这两个三角形中只有一组对应角相等, ∴△ABC和△DEF不一定全等,故B不符合题意; ∵ AB=EF,∠A=∠D,AC=DF ,EF和DF的夹角为∠F, ∴△ABC和△DEF不全等,故C不符合题意; ∵ BC=EF,∠C=∠F,AC=DF ∴△ABC≌△DEF(SAS),故D符合题意; 故答案为:D 【分析】利用判定两三角形全等的方法:SSS,SAS,AAS,ASA,对各选项逐一判断,即可得出答案:注意对应边和对应角。2-1-c-n-j-y
2. D
解:A、∵∠BAD=∠CAD,
∴ ,
∴△ABD≌△ACD(ASA);故不符合题意;
B、∵∠B=∠C,
∴??? ,
∴△ABD≌△ACD(AAS);故不符合题意;
C、∵BD=CD,
∴ ,
∴△ABD≌△ACD(SAS);故不符合题意;
D、AB=AC与∠ADB=∠ADC、AD=AD组成了SSA不能由此判定三角形全等,故符合题意。
故答案为:D。
【分析】根据题干及图形提供的条件来看,已经具有AD=AD, ,要使 只需要再添加任意一对角对应相等或BD=CD即可,从而即可一一判断得出答案。
二、填空题
3. ∠DAB=∠CBA或AC=BD
解:∵在△ABD和△BAC中, ∴△ABD≌△BAC(SAS),故可以添加∠DAB=∠CBA; 在△ABD和△BAC中, ∴△ABD≌△BAC(SAS),故可以添加AC=BD; 故答案为:∠DAB=∠CBA或AC=BD 【分析】观察图形,隐含条件为:AB=BA,因此利用SAS,可以添加∠DAB=∠CBA,利用SSS可以添加AC=BD.21世纪教育网版权所有
4. ①④
解:如图1,在BC上截取BH=BE,连接EH.
?
∵BE=BH,∠EBH=90°,
∴EH= BE,∵AF= BE,∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°,
∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,
∴AE=HC,∴△FAE≌△EHC(SAS),
∴EF=EC,∠AEF=∠ECH,
∵∠ECH+∠CEB=90°,∴∠AEF+∠CEB=90°,∴∠FEC=90°,
∴∠ECF=∠EFC=45°,故①正确,
如图2中,延长AD到H,使得DH=BE,则△CBE≌△CDH(SAS),
∴∠ECB=∠DCH,∴∠ECH=∠BCD=90°,∴∠ECG=∠GCH=45°,
∵CG=CG,CE=CH,∴△GCE≌△GCH(SAS),∴EG=GH,
∵GH=DG+DH,DH=BE,
∴EG=BE+DG,故③错误,
∴△AEG的周长=AE+EG+AG=AG+GH=AD+DH+AE=AE+EB+AD=AB+AD=2a,故②错误,
设BE=x,则AE=a-x,AF= ,
∴∴ ,
∴当 时, 的面积有最大值,最大值是 ,④正确;
故答案为:①④. 【分析】根据全等三角形的判定定理(AAS)和三角形的周长、面积公式,可列出关系式,得到正确的结论。21cnjy.com
5. BC=EF或∠BAC=∠EDF(答案不唯一)
解:∵ BC∥EF ∴∠B=∠E ∵BD=AE ∴ BD-AD=AE-AD,即BA=DE ∴添加BC=EF ∴△ABC≌△DEF(SAS) 添加 ∠BAC=∠EDF ∴△ABC≌△DEF(ASA) 添加∠C=∠F ∴△ABC≌△DEF(AAS) 故答案为: BC=EF或∠BAC=∠EDF或∠C=∠F www-2-1-cnjy-com
【分析】利用平行线的性质,易证∠B=∠E,再由BD=AE,再根据SAS或ASA或AAS添加条件即可得到△ABC≌△DEF。21*cnjy*com
6. OC=OD
理由是:在△AOC和△BOD中,
?
∴△AOC≌△BOD(SAS).
故答案为:OC=OD. 【分析】开放性的命题,答案不唯一,题干中已经具有 OA=OB ,图形中又具有∠AOC=∠BOD,故只要添加任意一组角对应相等,或边OC=OD即可利用三角形全等的判定方法判断出△AOC≌△BOD。
三、解答题
7. 解:∵AB∥DE,BC∥EF, ∴∠A=∠EDF,∠ACB=∠F, ∵AD=CF, ∴AD+DC=CF+CD即AC=DF; 在△ABC和△DEF中, ∴△ABC≌△DEF(SAS) 源【分析】利用平行线的性质,易证∠A=∠EDF,∠ACB=∠F,再利用线段的和差,可证得AC=DF,然后利用SAS可证得结论。【出处:21教育名师】
8. 证明:∵AB∥CD,
∴∠BAC=∠ECD,
在△BAC和△ECD中 ,
∴△BAC≌△ECD(SAS),
∴BC=ED
【分析】根据平行线的性质,即可得到∠BAC=∠ECD,根据边角边的三角形的判定定理即可证明三角形全等,得出BC=ED即可。【版权所有:21教育】
四、综合题
9. (1)证明:如图所示:
∵△ABC是等边三角形,
∴在△ABE和△CAD中,
AB=AC ;
∴△ABE≌△CAD(SAS) (2)证明:∵△ABE≌△CAD,
∴∠ABE=∠CAD,
又∵∠BAE=∠BAP+∠PAE=60°,
∴∠BAP+∠ABP=60°,
又∵∠BPF=∠BAP+∠ABP,
∴∠BPF=60°,
∵BF⊥AD
∴tan∠BPF= ,
∴tan60°= = ,
∴BF= PF
【分析】(1)在等边三角形ABC中,AB=AC,∠BAC=∠C=60°,且AE=CD,根据“两边和其夹角对应相等的两个三角形全等”可证明△ACD≌△BAE; (2)由题(1)可得∠CAD=∠ABE,故∠BPD=∠BAD+∠ABE=∠BAD+∠CAD=60°,由于BF⊥AD,根据三角函数可得tan∠BPF=, 所以可证明BF=PF。www.21-cn-jy.com
10. (1)t (2)证明:∵∠CFD=90°,∠B=90°,
∴DF∥AB,
∴∠AED=∠FDE.
在△AED和△FDE中,AF=FD=t,∠AED=∠FDE,DE=DE,
∴△AED≌△FDE(SAS). (3)∵△AED≌△FDE,
∴当△DEF是等边三角形时,△EDA是等边三角形.
∵∠A=90°﹣∠C=60°,
∴AD=AE.
∵AE=t,AD=AC﹣CD=10﹣2t,
∴t=10﹣2t,
∴t= ,
∴当t为 时,△DEF是等边三角形.
(4)∵△AED≌△FDE,
∴当△DEF为直角三角形时,△EDA是直角三角形.
当∠AED=90°时,AD=2AE,即10﹣2t=2t,
解得:t= ;
当∠ADE=90°时,AE=2AD,即t=2(10﹣2t),
解得:t=4.
综上所述:当t为 或4时,△DEF为直角三角形.
解:(1)∵DF⊥BC,
∴∠CFD=90°.
在Rt△CDF中,∠CFD=90°,∠C=30°,CD=2t,
∴DF= CD=t.
故答案为:t.
【分析】(1)根据30°的角所对的直角边等于斜边的一半可得DF= CD=t.(2)根据两直线平行内错角相等可得 ∠AED=∠FDE,由SAS即可判断△AED≌△FDE ;(3)由 △AED≌△FDE可知, 当△DEF是等边三角形时,△EDA是等边三角形,根据有一个角是60°的等腰三角形是等边三角形可得当 AD=AE,即 t=10﹣2t时, △DEF是等边三角形,解方程求出t值即可.(4)由△AED≌△FDE可知 ,当△DEF为直角三角形时,△EDA是直角三角形. ① 当∠ADE=90°时 ,根据30°的角所对的直角边等于斜边的一半可得 AE=2AD,即t=2(10﹣2t), 解方程求出t值即可.② 当∠AED=90°时,根据30°的角所对的直角边等于斜边的一半可得 AD=2AE,即10﹣2t=2t,解方程求出t值即可.【来源:21·世纪·教育·网】
