第一章勾股定理过关测试卷(无答案)

第一章过关测试
(第一章　勾股定理)
　　本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷30分,第Ⅱ卷70分, 共100分,考试时间100分钟.
第Ⅰ卷　(选择题　共30分)
　　　　　　　　　　　　　　　　　　　　　　
一、选择题(每小题3分,共30分)
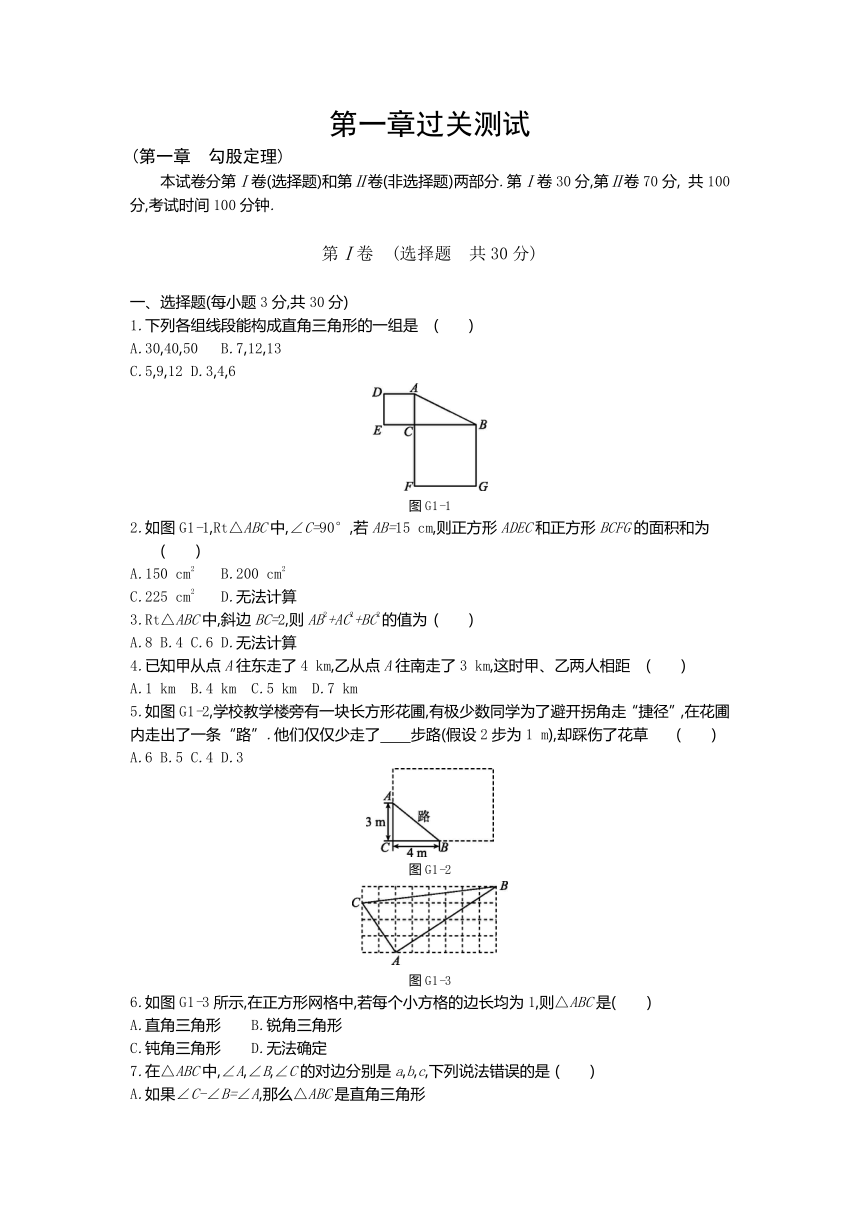
1.下列各组线段能构成直角三角形的一组是 (　　)
A.30,40,50 B.7,12,13
C.5,9,12 D.3,4,6
图G1-1
2.如图G1-1,Rt△ABC中,∠C=90°,若AB=15 cm,则正方形ADEC和正方形BCFG的面积和为 (　　)
A.150 cm2 B.200 cm2
C.225 cm2 D.无法计算
3.Rt△ABC中,斜边BC=2,则AB2+AC2+BC2的值为 (　　)
A.8 B.4 C.6 D.无法计算
4.已知甲从点A往东走了4 km,乙从点A往南走了3 km,这时甲、乙两人相距 (　　)
A.1 km B.4 km C.5 km D.7 km
5.如图G1-2,学校教学楼旁有一块长方形花圃,有极少数同学为了避开拐角走“捷径”,在花圃内走出了一条“路”.他们仅仅少走了　　步路(假设2步为1 m),却踩伤了花草 (　　)?
A.6 B.5 C.4 D.3
图G1-2
图G1-3
6.如图G1-3所示,在正方形网格中,若每个小方格的边长均为1,则△ABC是(　　)
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
7.在△ABC中,∠A,∠B,∠C的对边分别是a,b,c,下列说法错误的是 (　　)
A.如果∠C-∠B=∠A,那么△ABC是直角三角形
B.如果c2=b2-a2,那么△ABC是直角三角形,且∠C=90°
C.如果(c+a)(c-a)=b2,那么△ABC是直角三角形
D.如果∠A∶∠B∶∠C=5∶2∶3,那么△ABC是直角三角形
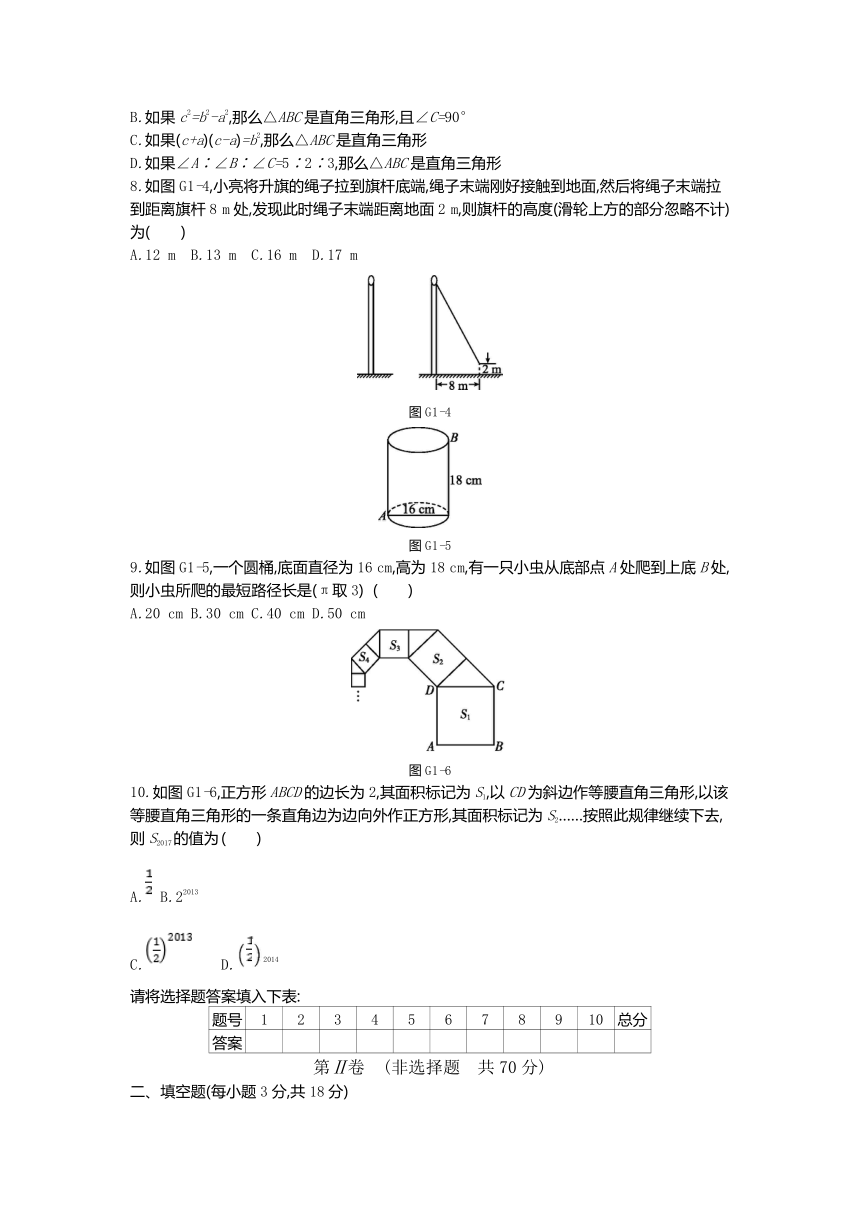
8.如图G1-4,小亮将升旗的绳子拉到旗杆底端,绳子末端刚好接触到地面,然后将绳子末端拉到距离旗杆8 m处,发现此时绳子末端距离地面2 m,则旗杆的高度(滑轮上方的部分忽略不计)为(　　)
A.12 m B.13 m C.16 m D.17 m
图G1-4
图G1-5
9.如图G1-5,一个圆桶,底面直径为16 cm,高为18 cm,有一只小虫从底部点A处爬到上底B处,则小虫所爬的最短路径长是(π取3) (　　)
A.20 cm B.30 cm C.40 cm D.50 cm
图G1-6
10.如图G1-6,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2……按照此规律继续下去,则S2017的值为 (　　)
A. B.22013
C. D.2014
请将选择题答案填入下表:
题号
1
2
3
4
5
6
7
8
9
10
总分
答案
第Ⅱ卷　(非选择题　共70分)
二、填空题(每小题3分,共18分)
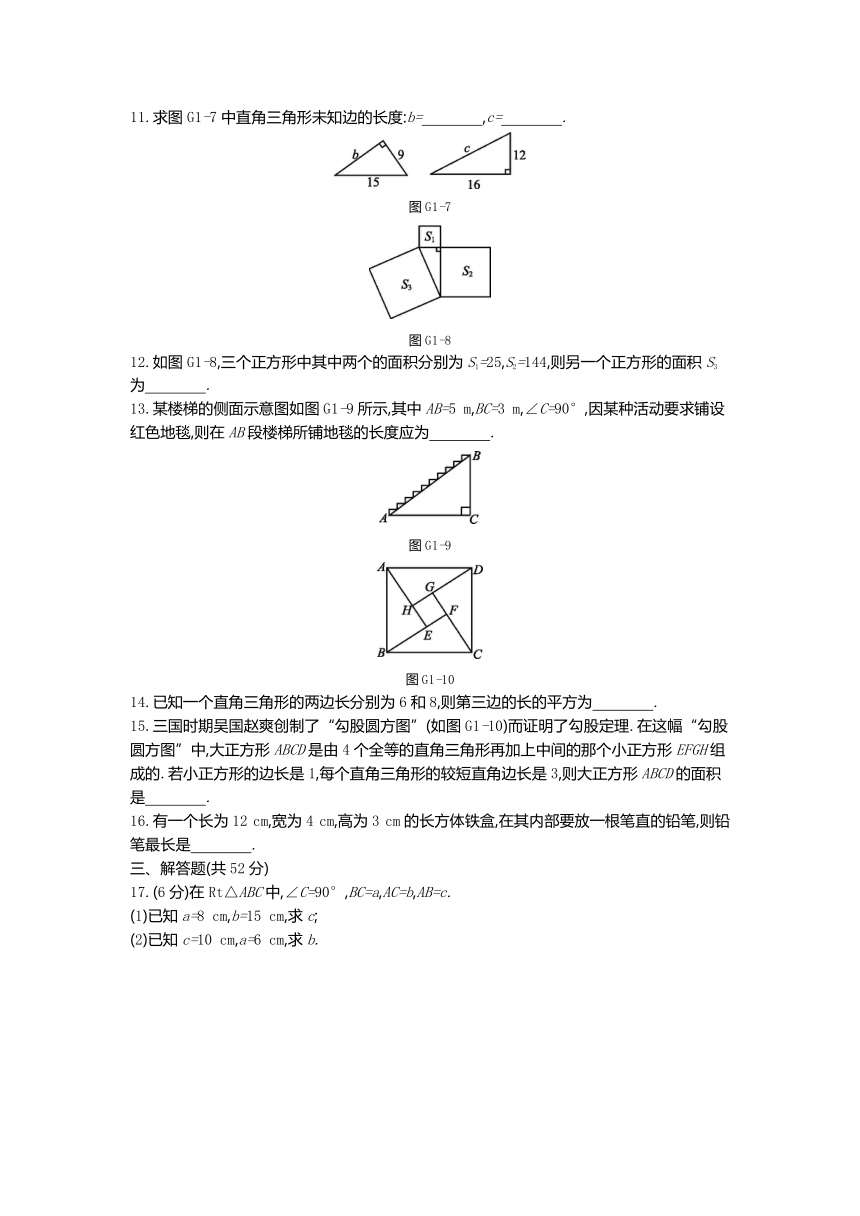
11.求图G1-7中直角三角形未知边的长度:b=　　　　,c=　　　　.?
图G1-7
图G1-8
12.如图G1-8,三个正方形中其中两个的面积分别为S1=25,S2=144,则另一个正方形的面积S3为　　　　.?
13.某楼梯的侧面示意图如图G1-9所示,其中AB=5 m,BC=3 m,∠C=90°,因某种活动要求铺设红色地毯,则在AB段楼梯所铺地毯的长度应为　　　　.?
图G1-9
图G1-10
14.已知一个直角三角形的两边长分别为6和8,则第三边的长的平方为　　　　.?
15.三国时期吴国赵爽创制了“勾股圆方图”(如图G1-10)而证明了勾股定理.在这幅“勾股圆方图”中,大正方形ABCD是由4个全等的直角三角形再加上中间的那个小正方形EFGH组成的.若小正方形的边长是1,每个直角三角形的较短直角边长是3,则大正方形ABCD的面积是　　　　.?
16.有一个长为12 cm,宽为4 cm,高为3 cm的长方体铁盒,在其内部要放一根笔直的铅笔,则铅笔最长是　　　　.?
三、解答题(共52分)
17.(6分)在Rt△ABC中,∠C=90°,BC=a,AC=b,AB=c.
(1)已知a=8 cm,b=15 cm,求c;
(2)已知c=10 cm,a=6 cm,求b.
18.(4分)如图G1-11,已知△ABC中,CD⊥AB于点D,AC=20,BC=15,DB=9,求AB的长.
图G1-11
19.(6分)如图G1-12所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8 cm,BC=10 cm.求CE的长.
图G1-12
20.(6分)小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5 m远的水底,竹竿高出水面0.5 m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,求河水的深度.
21.(6分)如图G1-13,两艘军舰在海上进行为时2小时的军事演习,一艘军舰以160海里/时的速度从港口A出发,向北偏东60°方向航行到达B处,另一艘军舰以120海里/时的速度同时从港口A出发,向南偏东30°方向航行到达C处,则此时两艘军舰相距多少海里?
图G1-13
22.(6分)如图G1-14所示,去年某省将位于A,B两地的两所大学合并成了一所综合性大学,为方便A,B两地师生的交往,学校准备在相距5 km的A,B两地之间修筑一条笔直的公路,已知有一个C地为中心,半径为2 km的果园,并且AC=4 km,BC=3 km,问计划修筑的这条公路会不会穿过该果园?为什么?
图G1-14
23.(8分)如图G1-15所示,为了丰富少年儿童的业余文化生活,某社区要在AB所在的直线上建一个图书阅览室.本社区有两所学校,分别在点C和点D处.已知CA⊥AB于点A,DB⊥AB于点B,AB=25 km,CA=15 km,DB=10 km.试问:阅览室E应建在距点A多少千米处,才能使它到两所学校的距离相等?
图G1-15
24.(10分)有一个如图G1-16所示的长方体透明玻璃鱼缸,假设其长AD=80 cm,高AB=60 cm,水深AE=40 cm,在水面上紧贴内壁G处有一块面包屑,G在水面线EF上,且EG=60 cm.一只蚂蚁想从鱼缸外的点A沿缸壁爬进鱼缸内的G处吃面包屑.
(1)该蚂蚁应该沿怎样的路线爬行才能使路程最短呢?请你画出它爬行的路线,并用箭头标注.
(2)求蚂蚁爬行的最短路线长.
图G1-16