人教版九年级数学上册第二十四章 圆24.1.2 垂直于弦的直径教学课件(共30张PPT)
文档属性
| 名称 | 人教版九年级数学上册第二十四章 圆24.1.2 垂直于弦的直径教学课件(共30张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-31 00:00:00 | ||
图片预览







文档简介
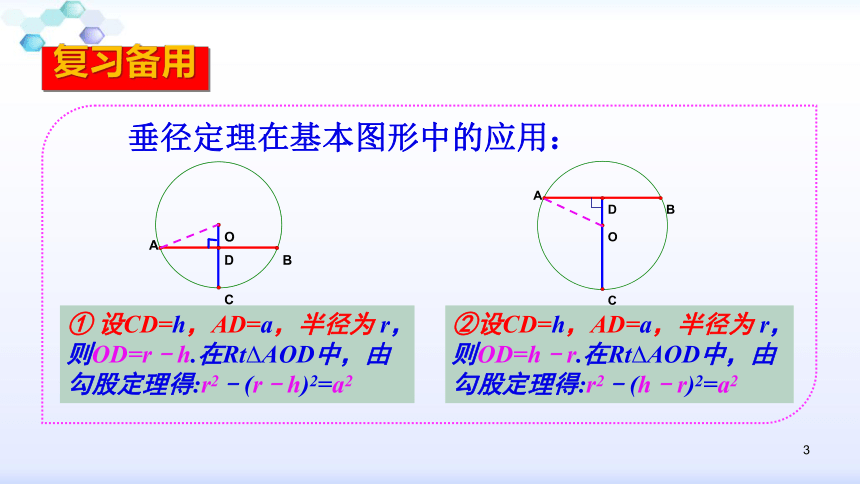
课件30张PPT。1几何语言复习备用2垂径定理的几个基本图形:复习备用3垂径定理在基本图形中的应用:① 设CD=h,AD=a,半径为 r,则OD=r﹣h.在Rt?AOD中,由勾股定理得:r2﹣(r﹣h)2=a2②设CD=h,AD=a,半径为 r,则OD=h﹣r.在Rt?AOD中,由勾股定理得:r2﹣(h﹣r)2=a2复习备用4几何语言复习备用 在一个圆中,一条直线只要满足下列五个条件中的任意两个,那么它一定具备其他三个:
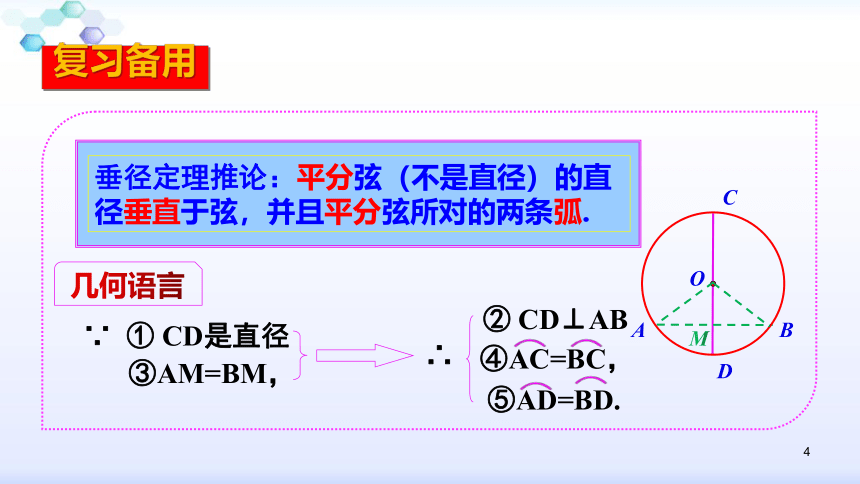
①过圆心 ②垂直于弦 ③平分弦(非直径) ④平分弦所对优弧 ⑤平分弦所对的劣弧
简称“知二推三”复习备用56人教版九年级数学上册第二十四章 圆24.1 圆的有关性质 1.2 ② 垂径定理的应用1.能灵活运用垂径定理及其推论进行证明和计算.
2.能利用垂径定理及其推论解决简单的实际问题.
3.能利用垂径定理解决最值问题.重点:利用垂径定理及其推论解决简单的实际问题.
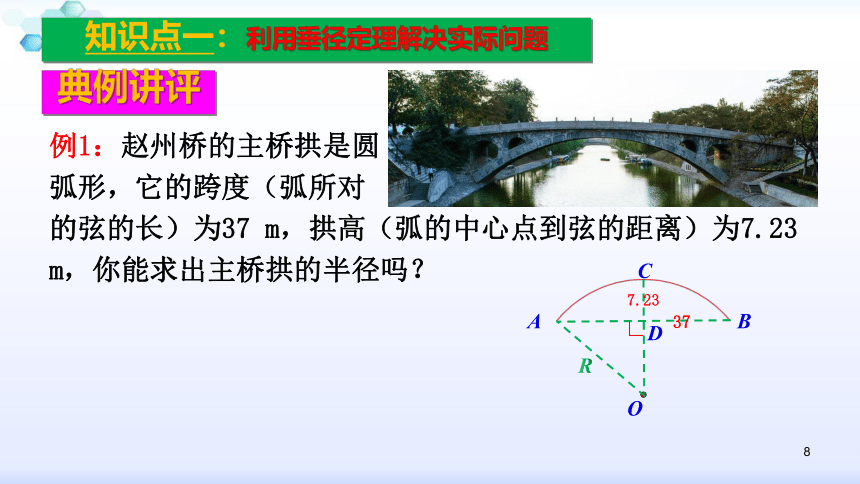
难点:利用垂径定理解决最值问题.7学习目标重点难点8例1:赵州桥的主桥拱是圆
弧形,它的跨度(弧所对
的弦的长)为37 m,拱高(弧的中心点到弦的距离)为7.23 m,你能求出主桥拱的半径吗? 知识点一:利用垂径定理解决实际问题典例讲评7.23379学以致用1.在直径为650mm的圆柱形油槽内装入一些油后,油面宽AB=600mm,求油的最大深度.知识点一:利用垂径定理解决实际问题ED(1)解:如图(1)过点O作OD⊥AB于E,连OB
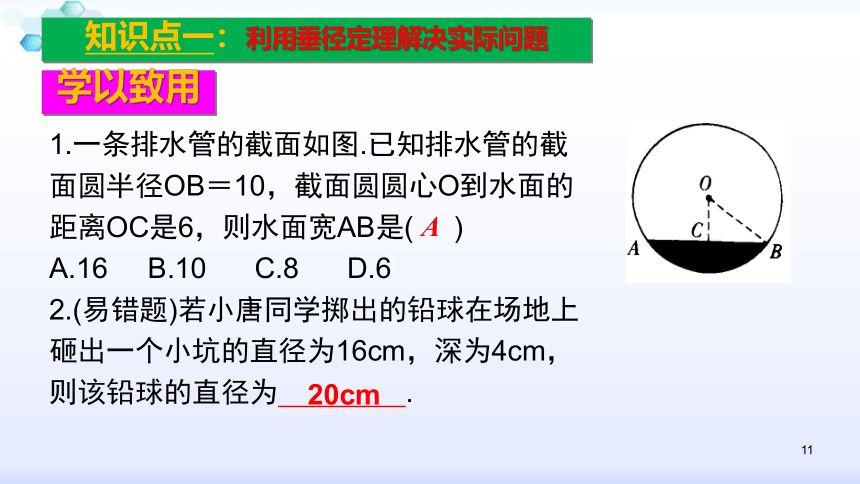
则在Rt?OBE中,由勾股定理得:=125(mm)∴油的最大深度ED=OD-OE=200(mm)10学以致用1.在直径为650mm的圆柱形油槽内装入一些油后,油面宽AB=600mm,求油的最大深度.知识点一:利用垂径定理解决实际问题解:如图(2)在Rt?OBE中,由勾股定理得:=125(mm)∴ED=OD+OE=450(mm)∴油的最大深度是200mm或450mm.111.一条排水管的截面如图.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是( )
A.16 B.10 C.8 D.6
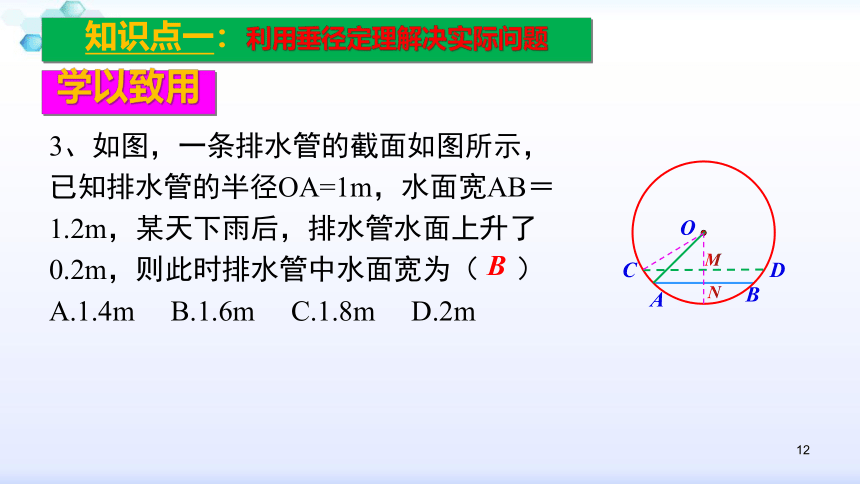
2.(易错题)若小唐同学掷出的铅球在场地上砸出一个小坑的直径为16cm,深为4cm,则该铅球的直径为 .A20cm学以致用知识点一:利用垂径定理解决实际问题123、如图,一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,排水管水面上升了0.2m,则此时排水管中水面宽为( )
A.1.4m B.1.6m C.1.8m D.2m学以致用知识点一:利用垂径定理解决实际问题MNB134、《九章算术》是我国古代第一部自成体系的数学专著.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸),问这块圆柱形木
材的直径是多少?”如图,请根据所学知
识计算:圆柱形木材的直径AC是( )
A13寸 B.20寸 C.26寸 D.28寸学以致用知识点一:利用垂径定理解决实际问题C145、如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米
(1)求圆弧所在圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?学以致用知识点一:利用垂径定理解决实际问题 先独立完成导学案互动探究2,再同桌相互交
流,最后小组交流;15合作探究知识点一:利用垂径定理解决实际问题16归纳总结知识点一:利用垂径定理解决实际问题17典例讲评知识点二:垂径定理与平面直角坐标系的综合应用例2:如图,在平面直角坐标系中,⊙P 的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P 截得的弦AB的长为 ,则a的值是( )
A.4 B. C. D.DE解析:如图,作PC⊥x轴于点C,交AB于点D,作PE⊥AB于点E,连接PBCxy18新知探究知识点二:垂径定理与平面直角坐标系的综合应用解析:如图,作PC⊥x轴于点C,交AB于点D,作PE⊥AB于点E,连接PB
∵⊙P的圆心坐标是(3,a),∴OC=3,PC=a.
把x=3代人y=x,得y=3 ∴CD=3,∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形.19学以致用知识点二:垂径定理与平面直角坐标系的综合应用1、如图,在平面直角坐标系中,A,B两点分别为圆P与x轴y轴的交点,有一直线l通过点P且与AB垂直,点C为l与y轴的交点.若A,B,C的坐标分别为(a,0),(0,4),(0,-5),且a<0,则a的值为( )
A. B. C.-8 D.-7A202.如图,在平面直角坐标系中,⊙O′与两坐标轴分别交于A,B,C,D四点,已知A(6,0),B(0,-3),C(-2,0),则点D的坐标是( )
A.(0,2) B.(0,3) C.(0,4) D.(0,5)C知识点二:垂径定理与平面直角坐标系的综合应用学以致用213.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为 ,则点P的坐标为 .B(3,2)知识点二:垂径定理与平面直角坐标系的综合应用学以致用22典例讲评知识点三:利用垂径定理解决分类讨论问题例3:已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是 .EFEF2cm或14cm先独立完成导学案互动探究2、3,再同桌相互交
流,最后小组交流;23学以致用知识点三:利用垂径定理解决分类讨论问题24典例讲评知识点四:利用垂径定理解决最值问题例4:如图所示,AB,CD是半径为10的⊙O的两条弦AB=16,CD=12,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上任意一点,则PA+PC的最小值为 .H利用圆的对称性和垂径定理把PA+PC的最小值转化为AD的长.25学以致用知识点四:利用垂径定理解决最值问题1、⊙O的半径是8,AB是⊙O的直径,M为AB上动点,AC=CD=BD,如图所示,则CM+DM的最小值为 .D26学以致用知识点四:利用垂径定理解决最值问题2.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线
y=kx-3k+4与⊙O交于B,C两点,则弦BC的长的最小值为 .BD27归纳总结知识点四:利用垂径定理解决最值问题28思维导图垂径定理的应用29 对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?蓦然回首301.课本第90页习题24.21第9、16题;
2.《导学测评》;作业布置
①过圆心 ②垂直于弦 ③平分弦(非直径) ④平分弦所对优弧 ⑤平分弦所对的劣弧
简称“知二推三”复习备用56人教版九年级数学上册第二十四章 圆24.1 圆的有关性质 1.2 ② 垂径定理的应用1.能灵活运用垂径定理及其推论进行证明和计算.
2.能利用垂径定理及其推论解决简单的实际问题.
3.能利用垂径定理解决最值问题.重点:利用垂径定理及其推论解决简单的实际问题.
难点:利用垂径定理解决最值问题.7学习目标重点难点8例1:赵州桥的主桥拱是圆
弧形,它的跨度(弧所对
的弦的长)为37 m,拱高(弧的中心点到弦的距离)为7.23 m,你能求出主桥拱的半径吗? 知识点一:利用垂径定理解决实际问题典例讲评7.23379学以致用1.在直径为650mm的圆柱形油槽内装入一些油后,油面宽AB=600mm,求油的最大深度.知识点一:利用垂径定理解决实际问题ED(1)解:如图(1)过点O作OD⊥AB于E,连OB
则在Rt?OBE中,由勾股定理得:=125(mm)∴油的最大深度ED=OD-OE=200(mm)10学以致用1.在直径为650mm的圆柱形油槽内装入一些油后,油面宽AB=600mm,求油的最大深度.知识点一:利用垂径定理解决实际问题解:如图(2)在Rt?OBE中,由勾股定理得:=125(mm)∴ED=OD+OE=450(mm)∴油的最大深度是200mm或450mm.111.一条排水管的截面如图.已知排水管的截面圆半径OB=10,截面圆圆心O到水面的距离OC是6,则水面宽AB是( )
A.16 B.10 C.8 D.6
2.(易错题)若小唐同学掷出的铅球在场地上砸出一个小坑的直径为16cm,深为4cm,则该铅球的直径为 .A20cm学以致用知识点一:利用垂径定理解决实际问题123、如图,一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,排水管水面上升了0.2m,则此时排水管中水面宽为( )
A.1.4m B.1.6m C.1.8m D.2m学以致用知识点一:利用垂径定理解决实际问题MNB134、《九章算术》是我国古代第一部自成体系的数学专著.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸),问这块圆柱形木
材的直径是多少?”如图,请根据所学知
识计算:圆柱形木材的直径AC是( )
A13寸 B.20寸 C.26寸 D.28寸学以致用知识点一:利用垂径定理解决实际问题C145、如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米
(1)求圆弧所在圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?学以致用知识点一:利用垂径定理解决实际问题 先独立完成导学案互动探究2,再同桌相互交
流,最后小组交流;15合作探究知识点一:利用垂径定理解决实际问题16归纳总结知识点一:利用垂径定理解决实际问题17典例讲评知识点二:垂径定理与平面直角坐标系的综合应用例2:如图,在平面直角坐标系中,⊙P 的圆心坐标是(3,a)(a>3),半径为3,函数y=x的图象被⊙P 截得的弦AB的长为 ,则a的值是( )
A.4 B. C. D.DE解析:如图,作PC⊥x轴于点C,交AB于点D,作PE⊥AB于点E,连接PBCxy18新知探究知识点二:垂径定理与平面直角坐标系的综合应用解析:如图,作PC⊥x轴于点C,交AB于点D,作PE⊥AB于点E,连接PB
∵⊙P的圆心坐标是(3,a),∴OC=3,PC=a.
把x=3代人y=x,得y=3 ∴CD=3,∴△OCD为等腰直角三角形,
∴△PED也为等腰直角三角形.19学以致用知识点二:垂径定理与平面直角坐标系的综合应用1、如图,在平面直角坐标系中,A,B两点分别为圆P与x轴y轴的交点,有一直线l通过点P且与AB垂直,点C为l与y轴的交点.若A,B,C的坐标分别为(a,0),(0,4),(0,-5),且a<0,则a的值为( )
A. B. C.-8 D.-7A202.如图,在平面直角坐标系中,⊙O′与两坐标轴分别交于A,B,C,D四点,已知A(6,0),B(0,-3),C(-2,0),则点D的坐标是( )
A.(0,2) B.(0,3) C.(0,4) D.(0,5)C知识点二:垂径定理与平面直角坐标系的综合应用学以致用213.如图,在平面直角坐标系中,点O为坐标原点,点P在第一象限,⊙P与x轴交于O,A两点,点A的坐标为(6,0),⊙P的半径为 ,则点P的坐标为 .B(3,2)知识点二:垂径定理与平面直角坐标系的综合应用学以致用22典例讲评知识点三:利用垂径定理解决分类讨论问题例3:已知⊙O的半径为10cm,AB,CD是⊙O的两条弦,AB∥CD,AB=16cm,CD=12cm,则弦AB和CD之间的距离是 .EFEF2cm或14cm先独立完成导学案互动探究2、3,再同桌相互交
流,最后小组交流;23学以致用知识点三:利用垂径定理解决分类讨论问题24典例讲评知识点四:利用垂径定理解决最值问题例4:如图所示,AB,CD是半径为10的⊙O的两条弦AB=16,CD=12,MN是直径,AB⊥MN于点E,CD⊥MN于点F,P为EF上任意一点,则PA+PC的最小值为 .H利用圆的对称性和垂径定理把PA+PC的最小值转化为AD的长.25学以致用知识点四:利用垂径定理解决最值问题1、⊙O的半径是8,AB是⊙O的直径,M为AB上动点,AC=CD=BD,如图所示,则CM+DM的最小值为 .D26学以致用知识点四:利用垂径定理解决最值问题2.如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线
y=kx-3k+4与⊙O交于B,C两点,则弦BC的长的最小值为 .BD27归纳总结知识点四:利用垂径定理解决最值问题28思维导图垂径定理的应用29 对自己说,你有什么收获?
对同学说,你有什么温馨提示?
对老师说,你还有什么困惑?蓦然回首301.课本第90页习题24.21第9、16题;
2.《导学测评》;作业布置
同课章节目录
