2018~2019学年上海市普陀区九年级上册期中考试数学试卷(PDF版含答案)
文档属性
| 名称 | 2018~2019学年上海市普陀区九年级上册期中考试数学试卷(PDF版含答案) | 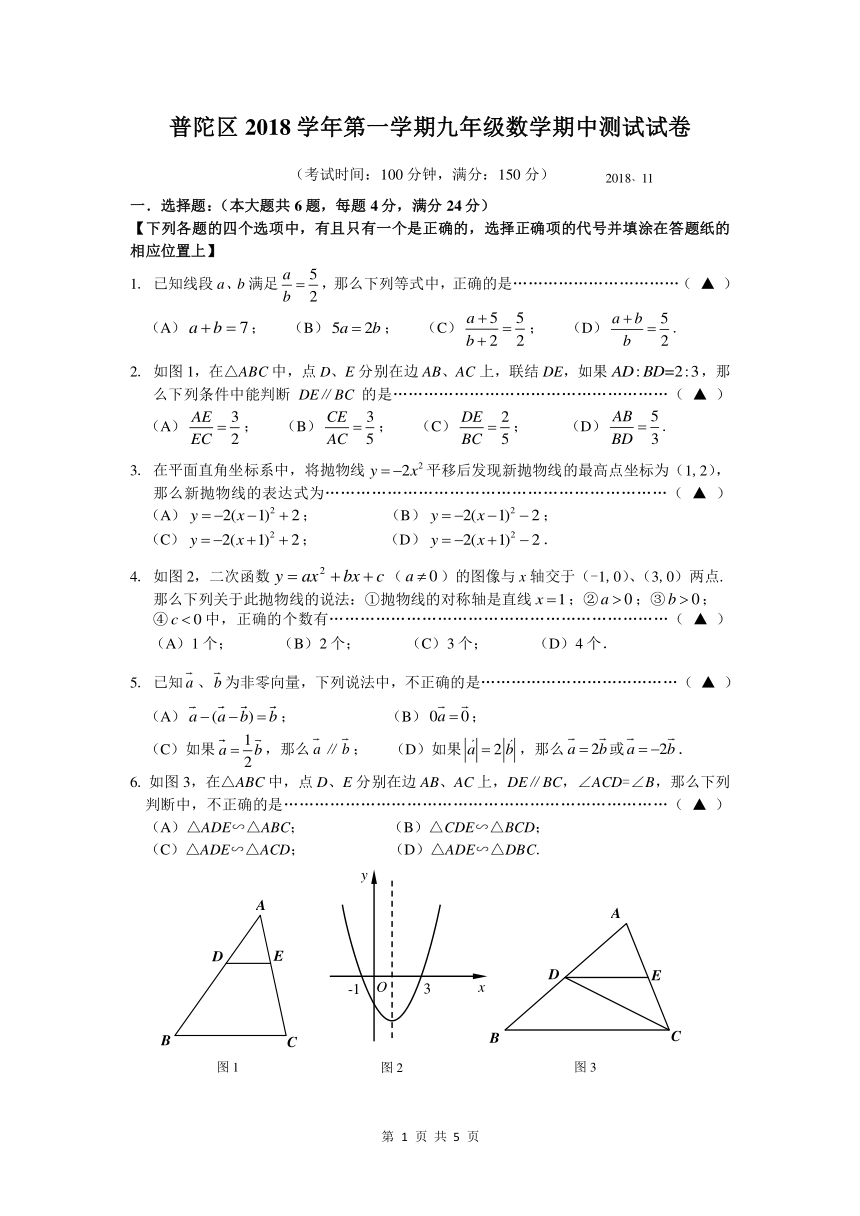 | |
| 格式 | zip | ||
| 文件大小 | 257.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-30 08:42:42 | ||
图片预览



文档简介
第 1 页 共 5 页
普陀区 2018 学年第一学期九年级数学期中测试试卷
(考试时间:100 分钟,满分:150 分) 2018、11
一.选择题:(本大题共 6 题,每题 4 分,满分 24 分)
【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的
相应位置上】
1. 已知线段 a、b 满足
5
2
a
b
? ,那么下列等式中,正确的是……………………………( ▲ )
(A) 7??ba ; (B) 5 2a b? ; (C) 5 5
2 2
a
b
?
?
?
; (D)
5
2
a b
b
?
? .
2. 如图 1,在△ABC 中,点 D、E 分别在边 AB、AC 上,联结 DE,如果 : =2:3AD BD ,那
么下列条件中能判断 DE∥BC 的是………………………………………………( ▲ )
(A)
3
2
AE
EC
? ; (B)
3
5
CE
AC
? ; (C)
2
5
DE
BC
? ; (D)
5
3
AB
BD
? .
3. 在平面直角坐标系中,将抛物线 22y x? ? 平移后发现新抛物线的最高点坐标为(1,2),
那么新抛物线的表达式为…………………………………………………………( ▲ )
(A) 22( 1) 2y x? ? ? ? ; (B) 22( 1) 2y x? ? ? ? ;
(C) 22( 1) 2y x? ? ? ? ; (D) 22( 1) 2y x? ? ? ? .
4. 如图 2,二次函数 cbxaxy ??? 2 ( 0a ? )的图像与 x 轴交于(-1,0)、(3,0)两点.
那么下列关于此抛物线的说法:①抛物线的对称轴是直线 1x ? ;② 0a ? ;③ 0b ? ;
④ 0c ? 中,正确的个数有…………………………………………………………( ▲ )
(A)1 个; (B)2 个; (C)3 个; (D)4 个.
5. 已知 a 、b 为非零向量,下列说法中,不正确的是…………………………………( ▲ )
(A) ( )a a b b? ? ? ; (B) 0 0a ? ;
(C)如果
1
2
a b? ,那么 a ∥b ; (D)如果 2a b? ,那么 2a b? 或 2a b? ? .
6. 如图 3,在△ABC 中,点 D、E 分别在边 AB、AC 上,DE∥BC,∠ACD=∠B,那么下列
判断中,不正确的是…………………………………………………………………( ▲ )
(A)△ADE∽△ABC; (B)△CDE∽△BCD;
(C)△ADE∽△ACD; (D)△ADE∽△DBC.
O
y
图 2
x 3 -1
ED
A
B C
图 3
ED
A
B C
图 1
第 2 页 共 5 页
二.填空题:(本大题共 12 题,每题 4 分,满分 48 分)
【请将结果直接填入答题纸的相应位置】
7. 如果线段 m 是线段 a、b、c 的第四比例项,已知 4a ? , 5b ? , 8c ? ,那么线段 m 的长
等于 ▲ .
8. 已知点 P 是线段 AB 的黄金分割点,且 AP > BP,如果 2 5 2AP ? ? ,那么 AB= ▲ .
9. 如果向量 a 与单位向量 e 的方向相反,且 | | 4 | |a e? ,那么 a = ▲ .(用 e 表示)
10. 已知点 A(3,n)在二次函数 2 2 3y x x? ? ? 的图像上,那么 n 的值为 ▲ .
11. 如果二次函数 ? ?22 4 3y x m x? ? ? ? ? 图像的对称轴是 y 轴,那么 m = ▲ .
12. 沿着 x 轴正方向看,抛物线 22y x bx c? ? ? 在对称轴左侧部分是 ▲ 的.(填“上
升”或“下降”)
13. 如图 4,AC、BD 相交于点 O,分别联结 AB、DC,如果∠A=∠D,OA=2,OB=5,
OD=
6
5
,那么 OC= ▲ .
14. 如图 5,△ABC 的中线 AD、BE 相交于点 G,过点 G 作 GH∥AC 交 BC 于点 H,
如果 GH=2,那么 AC = ▲ .
15. 如图 6,梯形 ABCD 中,AD∥BC,AC 与 BD 相交于点 O,
已知 Δ
Δ
1
4
AOD
COB
S
S
? ,那么 Δ
Δ
AOD
AOB
S
S
= ▲ .
16. 如图 7,在△ABC 中,点 D、E 分别在边 AB、AC 的反向延长线上,
DE∥BC,
1
2
AD
AB
? ,设 AB a? , AC b? ,那么向量 DE 用向量
a 、 b 表示为 ▲ .
17. 如果抛物线 L:
2
y ax bx c? ? ? (其中 a、b、c 是常数,且 0?a )与直线 l 都经过 y
轴上的同一点,且抛物线的顶点 P 在直线 l 上,那么称该直线 l 是抛物线 L 的“梦想直
线”.如果直线 l: 1y nx? ? (n 是常数)是抛物线 L: 2 2y x x m? ? ? (m 是常数)
的“梦想直线”,那么 m n? 的值是 ▲ .
18. 如图 8,在△ABC 中,AB=6,BC=4,AC=3,
将△ABC 绕点 A 旋转得到△AEF,点 E、F
分别是点 B、C 旋转后得到的点,如果 AF∥BC,
直线 AE 交 BC 的延长线于点 D,那么 DE 的长
为 ▲ .
H
G
E
D
A
B C
图 5
E
A
B C
D
图 7
D
O
A
C
B 图 4
O
D
B C
A
图 6
A
CB 图 8
第 3 页 共 5 页
三.解答题(本大题共 7 题,满分 78 分)
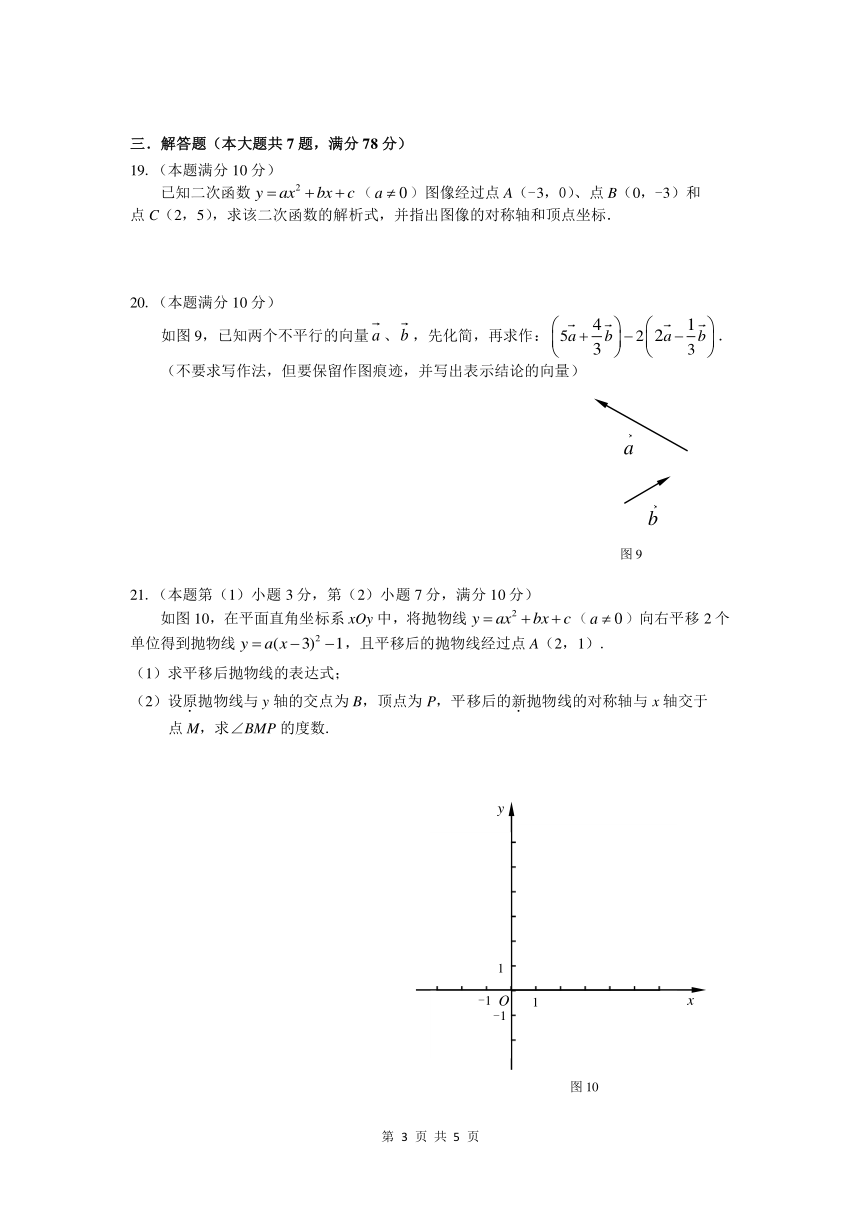
19.(本题满分 10 分)
已知二次函数 2y ax bx c? ? ? ( 0?a )图像经过点 A(-3,0)、点 B(0,-3)和
点 C(2,5),求该二次函数的解析式,并指出图像的对称轴和顶点坐标.
20.(本题满分 10 分)
如图 9,已知两个不平行的向量 a 、b ,先化简,再求作: 5 2
3
4 1
2
3
a b a b? ? ?? ? ? ?? ? ? ?
? ? ? ?
.
(不要求写作法,但要保留作图痕迹,并写出表示结论的向量)
21.(本题第(1)小题 3 分,第(2)小题 7 分,满分 10 分)
如图 10,在平面直角坐标系 xOy 中,将抛物线 2y ax bx c? ? ? ( 0?a )向右平移 2 个
单位得到抛物线 2( 3) 1y a x? ? ? ,且平移后的抛物线经过点 A(2,1).
(1)求平移后抛物线的表达式;
(2)设原.抛物线与 y 轴的交点为 B,顶点为 P,平移后的新.抛物线的对称轴与 x 轴交于
点 M,求∠BMP 的度数.
a
b
图 9
y
x
图 10
O 1
1
-1
-1
第 4 页 共 5 页
22.(本题第(1)小题 4 分,第(2)小题 6 分,满分 10 分)
如图 11,在平行四边形 ABCD 中,点 G 在边 DC 的延长线上,AG 交边 BC 于点 E,交
对角线 BD 于点 F.
(1)求证: 2AF EF FG? ? ;
(2)如果
3
2
EF ? ,
8
3
FG ? ,求
BE
EC
的值.
23.(本题第(1)题 6 分,第(2)题 6 分,满分 12 分)
如图 12,在 Rt△ABC 中,∠ACB =90°,CD⊥AB 于点 D,E 是 AC 的中点,DE 的延长
线与 BC 的延长线交于点 F.
(1)求证:△FDC∽△FBD;
(2)求证: AC BF BC DF? ? ? .
24.(本题第(1)题 5 分,第(2)题 7 分,满分 12 分)
如图 13,在平面直角坐标系 xOy 中,抛物线与 x 轴的正半轴交于点 B(3,0),交 y 轴
于点 C,顶点 A(1,-4),直线 AB 与 y 轴交于点 D.
(1)求抛物线的表达式;
(2)联结 BC,如果点 P 在 x 轴上,且△PBC 与△BCD 相似,求出点 P 坐标.
F
E
D
C B
A
图 12
E
F
A D
B C
G
图 11
O
y
x
C
D
A
B
图 13
第 5 页 共 5 页
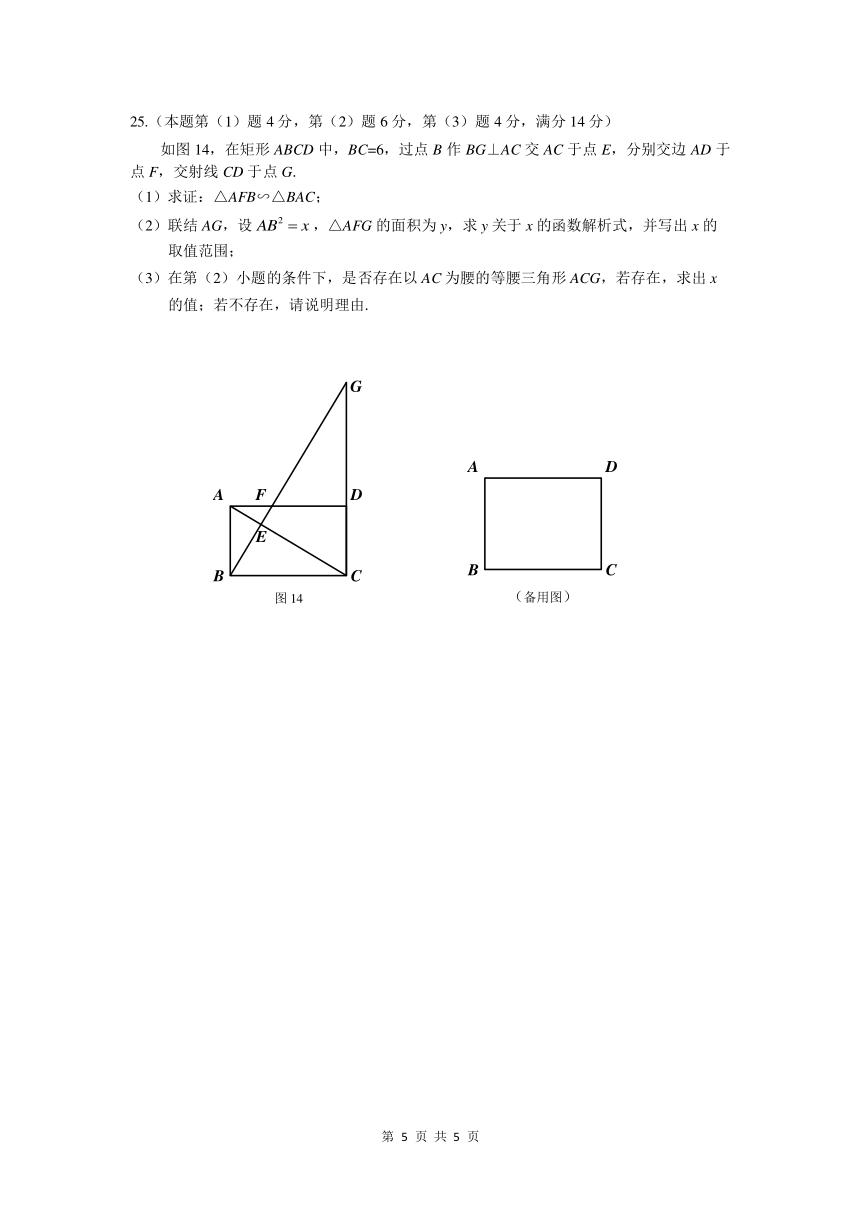
25.(本题第(1)题 4 分,第(2)题 6 分,第(3)题 4 分,满分 14 分)
如图 14,在矩形 ABCD 中,BC=6,过点 B 作 BG⊥AC 交 AC 于点 E,分别交边 AD 于
点 F,交射线 CD 于点 G.
(1)求证:△AFB∽△BAC;
(2)联结 AG,设 2AB x? ,△AFG 的面积为 y,求 y 关于 x 的函数解析式,并写出 x 的
取值范围;
(3)在第(2)小题的条件下,是否存在以 AC 为腰的等腰三角形 ACG,若存在,求出 x
的值;若不存在,请说明理由.
图 14
G
F
E
D
CB
A
(备用图)
D
CB
A
第 1 页共 6 页
普陀区 2018 学年第一学期九年级数学期中测试试卷评分标准 2018、11
一.选择题:
1.C; 2.B; 3.A; 4.C; 5.D; 6.D.
二.填空题:
7.10; 8.4; 9. 4e? ; 10.6; 11.4; 12.下降; 13.3; 14.6;
15.
1
2
; 16.
1 1
2 2
a b? ; 17.0; 18. 3
2
或
21
2
.
三、解答题:
19. 解:根据题意,得
9 3 0
3
4 2 5.
a b c
c
a b c
? ? ?
? ?
? ? ?
?
?
?
?
?
,
, ………………………………………………………… 3 分
解得
1
2
3
a
b
c
?
?
? ?
?
?
?
?
?
.…………………………………………………………………2 分
∴所求二次函数的解析式为
2
2 3y x x? ? ? .………………………………1 分
∴函数图像的对称轴为直线. 1x ? ? .……………………………………………2 分
顶点坐标为(-1,-4).……………………………………………………2 分
其中,函数图像对称轴为直线. 1x ? ? 中的“直线”不写扣 1 分.
20. 解:
1
5 2
3
4
2
3
a b a b? ? ?? ? ? ?? ? ? ?
? ? ? ?
5 4
3 3
4 2
a b a b? ? ? ?
...
……………………………………………………………2 分
2a b? ? ………………………………………………………………………2 分
作图如下:
∴OP即为所求作的向量.
其中,作图正确 2 分, a 和 2b 箭头正确各 1 分, 2a b? 箭头正确 1 分,结论 1 分.
O
A
P
a
2b
2a b?
第 2 页共 6 页
21. 解:(1)由题意,抛物线 2( 3) 1y a x? ? ? 经过点 A(2,1),
得 1 1a ? ? …………………………………………………………1 分
解得 2a ? …………………………………………………………1 分
∴平移后抛物线的表达式为 22( 3) 1y x? ? ? ..……………………1 分
(2)∵平移后抛物线的表达式为 22( 3) 1y x? ? ? ,
∴对称轴为直线. 3x ? .
∴点 M(3,0).……………………………………………………1 分
∵原抛物线向右平移 2 个单位得到抛物线 22( 3) 1y x? ? ? ,
∴原抛物线表达式为 22( 1) 1y x? ? ? .
∴顶点 P(1,-1).……………………………………………………1 分
∵抛物线 22( 1) 1y x? ? ? 与 y 轴相交于点 B,
∴点 B(0,1)..………………………………………………………1 分
∵B(0,1)、M(3,0)、P(1,-1),
∴ 5BP ? , 5MP ? , 10BM ? .
∴ 2 2 2BP MP BM? ? ,BP=MP.………………………………………1 分
∴△BPM 是等腰直角三角形,且∠BPM=90°.……………………2 分
∴∠BMP=45°.………………………………………………………1 分
22. (1)证明:∵四边形 ABCD 是平行四边形,
∴AB∥DC,AD∥BC.
∴
AF BF
GF DF
? ,
EF BF
AF DF
? .………………………………………1+1 分
∴
AF EF
GF AF
? .………………………………………………………1 分
即 2AF EF FG? ? .…………………………………………………1 分
(2)解:∵ 2AF EF FG? ? ,
又∵
3
2
EF ? ,
8
3
FG ? ,
∴ 2 4AF ? .
∴ 2AF ? .……………………………………………………………1 分
∵AD∥BC,
∴
BE EF
AD AF
? .…………………………………………………………1 分
∴
3
4
BE
AD
? .……………………………………………………………1 分
∵四边形 ABCD 是平行四边形,
∴AD=BC.
∴
3
4
BE
BC
? .……………………………………………………………1 分
第 3 页共 6 页
∴ 3
BE
EC
? .………………………………………………………………2 分
23.(1)证明:∵CD⊥AB,点 E 是 AC 的中点,
∴
1
2
CE DE AC? ? .
∴∠EDC=∠ECD.…………………………………………………1 分
∵CD⊥AB,∠ACB=90°,
∴∠ECD+∠A=90°,∠B+∠A=90°.
∴∠ECD=∠B.……………………………………………………2 分
∴∠EDC=∠B.……………………………………………………1 分
∵∠F=∠F,………………………………………………………1 分
∴△FDC∽△FBD.………………………………………………1 分
(2)证明:∵△FDC∽△FBD,
∴
DF DC
BF BD
? .………………………………………………… 2 分
∵CD⊥AB,
∴∠ADC=∠CDB=90°.
∵∠ECD=∠B,
∴△ADC∽△CDB.…………………………………………………1 分
∴
AC DC
CB DB
? .………………………………………………………1 分
∴
DF AC
BF CB
? .………………………………………………………1 分
即 AC BF BC DF? ? ? .…………………………………………………1 分
24. 解:(1)由题意设抛物线表达式为 2( 1) 4y a x? ? ? ( 0a ? ).……………2 分
∵抛物线交 x 轴于点 B(3,0),
∴得 4 4 0a ? ? ,……………………………………………………1 分
解得 1a ? .…………………………………………………………1 分
∴抛物线表达式为 2( 1) 4y x? ? ? .…………………………………1 分
(2)∵抛物线 2( 1) 4y x? ? ? 交 y 轴于点 C,
∴C(0,- 3).………………………………………………………1 分
∵B(3,0),
∴OC=OB=3.
联结 BC,
∵∠BOC =90°,
∴△BOC 是等腰直角三角形.
∴∠OBC=∠OCB=45°, 3 2BC ? .………………………………1 分
第 4 页共 6 页
设直线 AB 的表达式为 y kx b? ? ( 0k ? ),
∵直线 AB 经过点 A(1,-4)、B(3,0),
∴
4
3 0
k b
k b
? ? ??
? ? ??
,
解得
2
6
k
b
??
? ? ??
,
∴直线 AB 的表达式为 2 6y x? ? .
∵直线 AB 与 y 轴交于点 D,
∴D(0,-6),
∴CD=3.………………………………………………………………1 分
∵△PBC 与△BCD 相似,点 P 在 x 轴上,
又∵∠OBC=∠OCB=45°,
∴点 P 在点 B 右侧,且∠PBC=∠BCD=135°.……………………1 分
设 BP m? ,
①当
BP BC
CD CB
? 时,……………………………………………………1 分
得 1
3
m
? ,
解得 3m ? ,
∴点
1
P (6,0).………………………………………………………1 分
②当
BP BC
CB CD
? 时,
得
3 2
33 2
m
? ,
解得 6m ? ,
∴点
2
P (9,0).……………………………………………………1 分
综上所述,点 P 的坐标为(6,0)或(9,0).
备注:无论点
1
P 或
2
P ,哪个点先求解出,得分都为 2+1 分,但都必须先得出
线段比例关系.
25.(1)证明:∵四边形 ABCD 是矩形,
∴∠FAB=∠ABC=90°.……………………………………………1 分
∴∠ACB+∠BAC=90°.
∵BG⊥AC,
∴∠AEB=90°.
∴∠ABF+∠BAC=90°.
∴∠ABF=∠BCA.………………………………………………2 分
∴△AFB∽△BAC.………………………………………………1 分
(2)解:∵△AFB∽△BAC,
第 5 页共 6 页
∴
AF AB
BA BC
? .
即 2AB AF BC? ? .
∵ 2AB x? , 6BC ? ,
∴
6
x
AF ? .………………………………………………………1 分
∵四边形 ABCD 是矩形,
∴AB∥DC,AD=BC=6.
∴
AF AB
DF DG
? .
∵ 2AB x?
∴ AB x? (边长取正值).
∵
36
6
6 6
x x
DF
?
? ? ? ,
∴
36
x x
x DG
?
?
.
解得
(36 )x x
DG
x
?
? .…………………………………………2 分
∵
1
2
AFGS AF DG? ? ?△ ,且 AFGS y?△ ,
∴
1 (36 ) (36 )
2 6 12
x x x x x
y
x
? ?
? ? ? ? ( 0 36x? ? ).…… 2 + 1 分
(3)解:∵△ACG 是以 AC 为腰的等腰三角形,
①当 AC=AG 时,
解法 1:
∵AD⊥CG,
∴DC=DG.……………………………………………………………1 分
∵AB=DC,
∴AB=DG.
∴
(36 )x x
x
x
?
? ,
解得 18x ? .………………………………………………………1 分
解法 2:
∵AD⊥CG,
∴DC=DG.
∵AB=DC,
∴AB=DG.
∵
AF AB
DF DG
? ,
∴AF=DF.…………………………………………………………1 分
即
1
3
2
AF AD? ? .
∴ 3
6
x
? .
解得: 18x ? .……………………………………………………1 分
第 6 页共 6 页
②当 CA=CG 时,
解法 1:
∴ 2 2CA CG? .
∵∠ABC=90°,
∴ 2 2 2AB BC AC? ? .
即 2 36AC x? ? .
∵ AB DC x? ? ,
(36 )x x
DG
x
?
? ,
∴
(36 ) 36x x x
CG x
x x
?
? ? ? ,
∴ 2
36
36 ( )
x
x
x
? ? ,……………………………………………………1 分
化简得 2 236 36 0x x? ? ? ,
解得 18 18 5x ? ? ? .
∵ 2 0x AB? ? ,
∴ 18 5 18x ? ? ………………………………………………………1 分
解法 2:
∵CA=CG,
∴∠CAG=∠CGA.
∵AD∥BC,AB∥GC,
∴∠CAF=∠ACB,∠CGF=∠ABF.
∵∠ABF =∠ACB,
∴∠CAF =∠CGF.
∴AF=GF.
联结 CF,
∴△AFC≌△GFC.
∴∠AFC=∠GFC.
∵∠AFE=∠GFD,
∴∠AFC-∠AFE=∠GFC-∠GFD.
即∠EFC=∠DFC.
∵AD∥BC,
∴∠BCF=∠DFC.
∴∠BCF=∠EFC.
∴BF=BC=6.
∵∠BAF=90°,
∴ 2 2 2AF AB BF? ? .
即 2( ) 36
6
x
x? ? ,………………………………………………………1 分
化简得 2 236 36 0x x? ? ? ,
解得 18 18 5x ? ? ? .
∵ 2 0x AB? ? ,
∴ 18 5 18x ? ? ………………………………………………… 1 分
综上所述,x 的值为 18 或18 5 18? .
普陀区 2018 学年第一学期九年级数学期中测试试卷
(考试时间:100 分钟,满分:150 分) 2018、11
一.选择题:(本大题共 6 题,每题 4 分,满分 24 分)
【下列各题的四个选项中,有且只有一个是正确的,选择正确项的代号并填涂在答题纸的
相应位置上】
1. 已知线段 a、b 满足
5
2
a
b
? ,那么下列等式中,正确的是……………………………( ▲ )
(A) 7??ba ; (B) 5 2a b? ; (C) 5 5
2 2
a
b
?
?
?
; (D)
5
2
a b
b
?
? .
2. 如图 1,在△ABC 中,点 D、E 分别在边 AB、AC 上,联结 DE,如果 : =2:3AD BD ,那
么下列条件中能判断 DE∥BC 的是………………………………………………( ▲ )
(A)
3
2
AE
EC
? ; (B)
3
5
CE
AC
? ; (C)
2
5
DE
BC
? ; (D)
5
3
AB
BD
? .
3. 在平面直角坐标系中,将抛物线 22y x? ? 平移后发现新抛物线的最高点坐标为(1,2),
那么新抛物线的表达式为…………………………………………………………( ▲ )
(A) 22( 1) 2y x? ? ? ? ; (B) 22( 1) 2y x? ? ? ? ;
(C) 22( 1) 2y x? ? ? ? ; (D) 22( 1) 2y x? ? ? ? .
4. 如图 2,二次函数 cbxaxy ??? 2 ( 0a ? )的图像与 x 轴交于(-1,0)、(3,0)两点.
那么下列关于此抛物线的说法:①抛物线的对称轴是直线 1x ? ;② 0a ? ;③ 0b ? ;
④ 0c ? 中,正确的个数有…………………………………………………………( ▲ )
(A)1 个; (B)2 个; (C)3 个; (D)4 个.
5. 已知 a 、b 为非零向量,下列说法中,不正确的是…………………………………( ▲ )
(A) ( )a a b b? ? ? ; (B) 0 0a ? ;
(C)如果
1
2
a b? ,那么 a ∥b ; (D)如果 2a b? ,那么 2a b? 或 2a b? ? .
6. 如图 3,在△ABC 中,点 D、E 分别在边 AB、AC 上,DE∥BC,∠ACD=∠B,那么下列
判断中,不正确的是…………………………………………………………………( ▲ )
(A)△ADE∽△ABC; (B)△CDE∽△BCD;
(C)△ADE∽△ACD; (D)△ADE∽△DBC.
O
y
图 2
x 3 -1
ED
A
B C
图 3
ED
A
B C
图 1
第 2 页 共 5 页
二.填空题:(本大题共 12 题,每题 4 分,满分 48 分)
【请将结果直接填入答题纸的相应位置】
7. 如果线段 m 是线段 a、b、c 的第四比例项,已知 4a ? , 5b ? , 8c ? ,那么线段 m 的长
等于 ▲ .
8. 已知点 P 是线段 AB 的黄金分割点,且 AP > BP,如果 2 5 2AP ? ? ,那么 AB= ▲ .
9. 如果向量 a 与单位向量 e 的方向相反,且 | | 4 | |a e? ,那么 a = ▲ .(用 e 表示)
10. 已知点 A(3,n)在二次函数 2 2 3y x x? ? ? 的图像上,那么 n 的值为 ▲ .
11. 如果二次函数 ? ?22 4 3y x m x? ? ? ? ? 图像的对称轴是 y 轴,那么 m = ▲ .
12. 沿着 x 轴正方向看,抛物线 22y x bx c? ? ? 在对称轴左侧部分是 ▲ 的.(填“上
升”或“下降”)
13. 如图 4,AC、BD 相交于点 O,分别联结 AB、DC,如果∠A=∠D,OA=2,OB=5,
OD=
6
5
,那么 OC= ▲ .
14. 如图 5,△ABC 的中线 AD、BE 相交于点 G,过点 G 作 GH∥AC 交 BC 于点 H,
如果 GH=2,那么 AC = ▲ .
15. 如图 6,梯形 ABCD 中,AD∥BC,AC 与 BD 相交于点 O,
已知 Δ
Δ
1
4
AOD
COB
S
S
? ,那么 Δ
Δ
AOD
AOB
S
S
= ▲ .
16. 如图 7,在△ABC 中,点 D、E 分别在边 AB、AC 的反向延长线上,
DE∥BC,
1
2
AD
AB
? ,设 AB a? , AC b? ,那么向量 DE 用向量
a 、 b 表示为 ▲ .
17. 如果抛物线 L:
2
y ax bx c? ? ? (其中 a、b、c 是常数,且 0?a )与直线 l 都经过 y
轴上的同一点,且抛物线的顶点 P 在直线 l 上,那么称该直线 l 是抛物线 L 的“梦想直
线”.如果直线 l: 1y nx? ? (n 是常数)是抛物线 L: 2 2y x x m? ? ? (m 是常数)
的“梦想直线”,那么 m n? 的值是 ▲ .
18. 如图 8,在△ABC 中,AB=6,BC=4,AC=3,
将△ABC 绕点 A 旋转得到△AEF,点 E、F
分别是点 B、C 旋转后得到的点,如果 AF∥BC,
直线 AE 交 BC 的延长线于点 D,那么 DE 的长
为 ▲ .
H
G
E
D
A
B C
图 5
E
A
B C
D
图 7
D
O
A
C
B 图 4
O
D
B C
A
图 6
A
CB 图 8
第 3 页 共 5 页
三.解答题(本大题共 7 题,满分 78 分)
19.(本题满分 10 分)
已知二次函数 2y ax bx c? ? ? ( 0?a )图像经过点 A(-3,0)、点 B(0,-3)和
点 C(2,5),求该二次函数的解析式,并指出图像的对称轴和顶点坐标.
20.(本题满分 10 分)
如图 9,已知两个不平行的向量 a 、b ,先化简,再求作: 5 2
3
4 1
2
3
a b a b? ? ?? ? ? ?? ? ? ?
? ? ? ?
.
(不要求写作法,但要保留作图痕迹,并写出表示结论的向量)
21.(本题第(1)小题 3 分,第(2)小题 7 分,满分 10 分)
如图 10,在平面直角坐标系 xOy 中,将抛物线 2y ax bx c? ? ? ( 0?a )向右平移 2 个
单位得到抛物线 2( 3) 1y a x? ? ? ,且平移后的抛物线经过点 A(2,1).
(1)求平移后抛物线的表达式;
(2)设原.抛物线与 y 轴的交点为 B,顶点为 P,平移后的新.抛物线的对称轴与 x 轴交于
点 M,求∠BMP 的度数.
a
b
图 9
y
x
图 10
O 1
1
-1
-1
第 4 页 共 5 页
22.(本题第(1)小题 4 分,第(2)小题 6 分,满分 10 分)
如图 11,在平行四边形 ABCD 中,点 G 在边 DC 的延长线上,AG 交边 BC 于点 E,交
对角线 BD 于点 F.
(1)求证: 2AF EF FG? ? ;
(2)如果
3
2
EF ? ,
8
3
FG ? ,求
BE
EC
的值.
23.(本题第(1)题 6 分,第(2)题 6 分,满分 12 分)
如图 12,在 Rt△ABC 中,∠ACB =90°,CD⊥AB 于点 D,E 是 AC 的中点,DE 的延长
线与 BC 的延长线交于点 F.
(1)求证:△FDC∽△FBD;
(2)求证: AC BF BC DF? ? ? .
24.(本题第(1)题 5 分,第(2)题 7 分,满分 12 分)
如图 13,在平面直角坐标系 xOy 中,抛物线与 x 轴的正半轴交于点 B(3,0),交 y 轴
于点 C,顶点 A(1,-4),直线 AB 与 y 轴交于点 D.
(1)求抛物线的表达式;
(2)联结 BC,如果点 P 在 x 轴上,且△PBC 与△BCD 相似,求出点 P 坐标.
F
E
D
C B
A
图 12
E
F
A D
B C
G
图 11
O
y
x
C
D
A
B
图 13
第 5 页 共 5 页
25.(本题第(1)题 4 分,第(2)题 6 分,第(3)题 4 分,满分 14 分)
如图 14,在矩形 ABCD 中,BC=6,过点 B 作 BG⊥AC 交 AC 于点 E,分别交边 AD 于
点 F,交射线 CD 于点 G.
(1)求证:△AFB∽△BAC;
(2)联结 AG,设 2AB x? ,△AFG 的面积为 y,求 y 关于 x 的函数解析式,并写出 x 的
取值范围;
(3)在第(2)小题的条件下,是否存在以 AC 为腰的等腰三角形 ACG,若存在,求出 x
的值;若不存在,请说明理由.
图 14
G
F
E
D
CB
A
(备用图)
D
CB
A
第 1 页共 6 页
普陀区 2018 学年第一学期九年级数学期中测试试卷评分标准 2018、11
一.选择题:
1.C; 2.B; 3.A; 4.C; 5.D; 6.D.
二.填空题:
7.10; 8.4; 9. 4e? ; 10.6; 11.4; 12.下降; 13.3; 14.6;
15.
1
2
; 16.
1 1
2 2
a b? ; 17.0; 18. 3
2
或
21
2
.
三、解答题:
19. 解:根据题意,得
9 3 0
3
4 2 5.
a b c
c
a b c
? ? ?
? ?
? ? ?
?
?
?
?
?
,
, ………………………………………………………… 3 分
解得
1
2
3
a
b
c
?
?
? ?
?
?
?
?
?
.…………………………………………………………………2 分
∴所求二次函数的解析式为
2
2 3y x x? ? ? .………………………………1 分
∴函数图像的对称轴为直线. 1x ? ? .……………………………………………2 分
顶点坐标为(-1,-4).……………………………………………………2 分
其中,函数图像对称轴为直线. 1x ? ? 中的“直线”不写扣 1 分.
20. 解:
1
5 2
3
4
2
3
a b a b? ? ?? ? ? ?? ? ? ?
? ? ? ?
5 4
3 3
4 2
a b a b? ? ? ?
...
……………………………………………………………2 分
2a b? ? ………………………………………………………………………2 分
作图如下:
∴OP即为所求作的向量.
其中,作图正确 2 分, a 和 2b 箭头正确各 1 分, 2a b? 箭头正确 1 分,结论 1 分.
O
A
P
a
2b
2a b?
第 2 页共 6 页
21. 解:(1)由题意,抛物线 2( 3) 1y a x? ? ? 经过点 A(2,1),
得 1 1a ? ? …………………………………………………………1 分
解得 2a ? …………………………………………………………1 分
∴平移后抛物线的表达式为 22( 3) 1y x? ? ? ..……………………1 分
(2)∵平移后抛物线的表达式为 22( 3) 1y x? ? ? ,
∴对称轴为直线. 3x ? .
∴点 M(3,0).……………………………………………………1 分
∵原抛物线向右平移 2 个单位得到抛物线 22( 3) 1y x? ? ? ,
∴原抛物线表达式为 22( 1) 1y x? ? ? .
∴顶点 P(1,-1).……………………………………………………1 分
∵抛物线 22( 1) 1y x? ? ? 与 y 轴相交于点 B,
∴点 B(0,1)..………………………………………………………1 分
∵B(0,1)、M(3,0)、P(1,-1),
∴ 5BP ? , 5MP ? , 10BM ? .
∴ 2 2 2BP MP BM? ? ,BP=MP.………………………………………1 分
∴△BPM 是等腰直角三角形,且∠BPM=90°.……………………2 分
∴∠BMP=45°.………………………………………………………1 分
22. (1)证明:∵四边形 ABCD 是平行四边形,
∴AB∥DC,AD∥BC.
∴
AF BF
GF DF
? ,
EF BF
AF DF
? .………………………………………1+1 分
∴
AF EF
GF AF
? .………………………………………………………1 分
即 2AF EF FG? ? .…………………………………………………1 分
(2)解:∵ 2AF EF FG? ? ,
又∵
3
2
EF ? ,
8
3
FG ? ,
∴ 2 4AF ? .
∴ 2AF ? .……………………………………………………………1 分
∵AD∥BC,
∴
BE EF
AD AF
? .…………………………………………………………1 分
∴
3
4
BE
AD
? .……………………………………………………………1 分
∵四边形 ABCD 是平行四边形,
∴AD=BC.
∴
3
4
BE
BC
? .……………………………………………………………1 分
第 3 页共 6 页
∴ 3
BE
EC
? .………………………………………………………………2 分
23.(1)证明:∵CD⊥AB,点 E 是 AC 的中点,
∴
1
2
CE DE AC? ? .
∴∠EDC=∠ECD.…………………………………………………1 分
∵CD⊥AB,∠ACB=90°,
∴∠ECD+∠A=90°,∠B+∠A=90°.
∴∠ECD=∠B.……………………………………………………2 分
∴∠EDC=∠B.……………………………………………………1 分
∵∠F=∠F,………………………………………………………1 分
∴△FDC∽△FBD.………………………………………………1 分
(2)证明:∵△FDC∽△FBD,
∴
DF DC
BF BD
? .………………………………………………… 2 分
∵CD⊥AB,
∴∠ADC=∠CDB=90°.
∵∠ECD=∠B,
∴△ADC∽△CDB.…………………………………………………1 分
∴
AC DC
CB DB
? .………………………………………………………1 分
∴
DF AC
BF CB
? .………………………………………………………1 分
即 AC BF BC DF? ? ? .…………………………………………………1 分
24. 解:(1)由题意设抛物线表达式为 2( 1) 4y a x? ? ? ( 0a ? ).……………2 分
∵抛物线交 x 轴于点 B(3,0),
∴得 4 4 0a ? ? ,……………………………………………………1 分
解得 1a ? .…………………………………………………………1 分
∴抛物线表达式为 2( 1) 4y x? ? ? .…………………………………1 分
(2)∵抛物线 2( 1) 4y x? ? ? 交 y 轴于点 C,
∴C(0,- 3).………………………………………………………1 分
∵B(3,0),
∴OC=OB=3.
联结 BC,
∵∠BOC =90°,
∴△BOC 是等腰直角三角形.
∴∠OBC=∠OCB=45°, 3 2BC ? .………………………………1 分
第 4 页共 6 页
设直线 AB 的表达式为 y kx b? ? ( 0k ? ),
∵直线 AB 经过点 A(1,-4)、B(3,0),
∴
4
3 0
k b
k b
? ? ??
? ? ??
,
解得
2
6
k
b
??
? ? ??
,
∴直线 AB 的表达式为 2 6y x? ? .
∵直线 AB 与 y 轴交于点 D,
∴D(0,-6),
∴CD=3.………………………………………………………………1 分
∵△PBC 与△BCD 相似,点 P 在 x 轴上,
又∵∠OBC=∠OCB=45°,
∴点 P 在点 B 右侧,且∠PBC=∠BCD=135°.……………………1 分
设 BP m? ,
①当
BP BC
CD CB
? 时,……………………………………………………1 分
得 1
3
m
? ,
解得 3m ? ,
∴点
1
P (6,0).………………………………………………………1 分
②当
BP BC
CB CD
? 时,
得
3 2
33 2
m
? ,
解得 6m ? ,
∴点
2
P (9,0).……………………………………………………1 分
综上所述,点 P 的坐标为(6,0)或(9,0).
备注:无论点
1
P 或
2
P ,哪个点先求解出,得分都为 2+1 分,但都必须先得出
线段比例关系.
25.(1)证明:∵四边形 ABCD 是矩形,
∴∠FAB=∠ABC=90°.……………………………………………1 分
∴∠ACB+∠BAC=90°.
∵BG⊥AC,
∴∠AEB=90°.
∴∠ABF+∠BAC=90°.
∴∠ABF=∠BCA.………………………………………………2 分
∴△AFB∽△BAC.………………………………………………1 分
(2)解:∵△AFB∽△BAC,
第 5 页共 6 页
∴
AF AB
BA BC
? .
即 2AB AF BC? ? .
∵ 2AB x? , 6BC ? ,
∴
6
x
AF ? .………………………………………………………1 分
∵四边形 ABCD 是矩形,
∴AB∥DC,AD=BC=6.
∴
AF AB
DF DG
? .
∵ 2AB x?
∴ AB x? (边长取正值).
∵
36
6
6 6
x x
DF
?
? ? ? ,
∴
36
x x
x DG
?
?
.
解得
(36 )x x
DG
x
?
? .…………………………………………2 分
∵
1
2
AFGS AF DG? ? ?△ ,且 AFGS y?△ ,
∴
1 (36 ) (36 )
2 6 12
x x x x x
y
x
? ?
? ? ? ? ( 0 36x? ? ).…… 2 + 1 分
(3)解:∵△ACG 是以 AC 为腰的等腰三角形,
①当 AC=AG 时,
解法 1:
∵AD⊥CG,
∴DC=DG.……………………………………………………………1 分
∵AB=DC,
∴AB=DG.
∴
(36 )x x
x
x
?
? ,
解得 18x ? .………………………………………………………1 分
解法 2:
∵AD⊥CG,
∴DC=DG.
∵AB=DC,
∴AB=DG.
∵
AF AB
DF DG
? ,
∴AF=DF.…………………………………………………………1 分
即
1
3
2
AF AD? ? .
∴ 3
6
x
? .
解得: 18x ? .……………………………………………………1 分
第 6 页共 6 页
②当 CA=CG 时,
解法 1:
∴ 2 2CA CG? .
∵∠ABC=90°,
∴ 2 2 2AB BC AC? ? .
即 2 36AC x? ? .
∵ AB DC x? ? ,
(36 )x x
DG
x
?
? ,
∴
(36 ) 36x x x
CG x
x x
?
? ? ? ,
∴ 2
36
36 ( )
x
x
x
? ? ,……………………………………………………1 分
化简得 2 236 36 0x x? ? ? ,
解得 18 18 5x ? ? ? .
∵ 2 0x AB? ? ,
∴ 18 5 18x ? ? ………………………………………………………1 分
解法 2:
∵CA=CG,
∴∠CAG=∠CGA.
∵AD∥BC,AB∥GC,
∴∠CAF=∠ACB,∠CGF=∠ABF.
∵∠ABF =∠ACB,
∴∠CAF =∠CGF.
∴AF=GF.
联结 CF,
∴△AFC≌△GFC.
∴∠AFC=∠GFC.
∵∠AFE=∠GFD,
∴∠AFC-∠AFE=∠GFC-∠GFD.
即∠EFC=∠DFC.
∵AD∥BC,
∴∠BCF=∠DFC.
∴∠BCF=∠EFC.
∴BF=BC=6.
∵∠BAF=90°,
∴ 2 2 2AF AB BF? ? .
即 2( ) 36
6
x
x? ? ,………………………………………………………1 分
化简得 2 236 36 0x x? ? ? ,
解得 18 18 5x ? ? ? .
∵ 2 0x AB? ? ,
∴ 18 5 18x ? ? ………………………………………………… 1 分
综上所述,x 的值为 18 或18 5 18? .
同课章节目录
