上海市嘉定区2018-2019学年八年级上期中数学卷(pdf版,含答案)
文档属性
| 名称 | 上海市嘉定区2018-2019学年八年级上期中数学卷(pdf版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 229.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-30 00:00:00 | ||
图片预览


文档简介
2018 学年第一学期八年级期中考试
数学试题
(考试时间:90 分钟 满分 100 分) 2018.11
一、填空题(本大题共 14 题,每题 2 分,满分 28 分)
1.化简: 8 =_________.
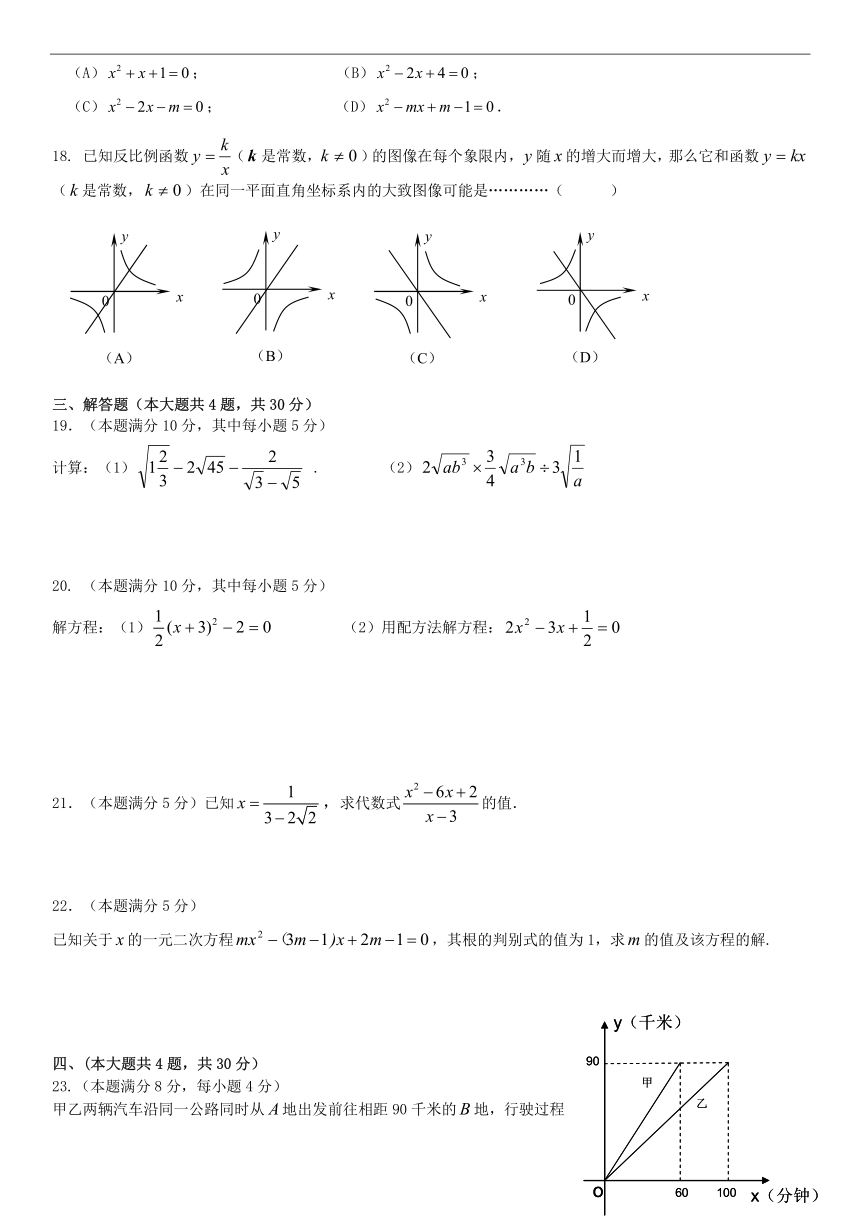
2.函数 2y x? ? 的定义域是___________.
3.化简: ba 2 (a <0)=____________.
4.计算: 18 8? = ___________.
5. ba ? 的一个有理化因式是___________.
6.不等式 132 ?xx> 的解集是___________.
7.方程 2 2x x? 的根是_____________________.
8.在实数范围内分解因式:
2 8 2x x? ? ? ____________________.
9.已知 3?x 是关于 x的方程 0122 ???? mx)m(x 的一个实数根,则m =_________.
10.如果正比例函数 x)k(y 23 ?? 的图像在第二、四象限内,那么 k 的取值范围是_________.
11.已知点 ),1( aA ? 、 ),1( bB 在函数
x
y
2
?? 的图像上,则a b (填“?”或“=”或“?”).
12. 如果
2
( )
2
x
f x
x
?
?
?
,那么 ( 2)f ? __________.
13. 某工厂七月份的产值是 100 万元,计划九月份的产值要达到 144 万元.如果每月产值的增长率相同,则这个增
长率是 .
14.对于实数m 、 n ,定义一种运算“?”为:m n mn n? ? ? .如果关于 x 的方程
1
( )
4
x a x? ? ? ? 有两个相
等的实数根,那么满足条件的实数a 的值是_______.
二、选择题(本大题共 4 题,每题 3 分,满分 12 分)
15. 下列二次根式中与 3 是同类二次根式的是……………………………( )
(A) 12 ; (B) 0.3 ; (C)
2
3
; (D) 18 ;
16.下列关于 x的方程一定是一元二次方程的是( )
(A) 02 ??? cbxax (B) xx ?? 53 2 (C)
22 51)75 xxx ???( (D) 01
12 ???
x
x
17.下列关于 x的方程中一定有实数解的是…………………………………( )
(A) 2 1 0x x? ? ? ; (B) 2 2 4 0x x? ? ? ;
(C) 2 2 0x x m? ? ? ; (D) 2 1 0x mx m? ? ? ? .
18. 已知反比例函数
x
k
y ? (k 是常数, 0?k )的图像在每个象限内,y 随 x 的增大而增大,那么它和函数 kxy ?
( k 是常数, 0?k )在同一平面直角坐标系内的大致图像可能是…………( )
三、解答题(本大题共 4 题,共 30 分)
19.(本题满分 10分,其中每小题 5分)
计算:(1)
53
2
452
3
2
1
?
?? . (2)
a
baab
1
3
4
3
2 33 ??
20. (本题满分 10分,其中每小题 5分)
解方程:(1)
21
( 3) 2 0
2
x ? ? ? (2)用配方法解方程: 0
2
1
32 2 ??? xx
21.(本题满分 5 分)已知
1
3 2 2
x ?
?
,求代数式
2
6 2
3
x x
x
? ?
?
的值.
22.(本题满分 5 分)
已知关于 x 的一元二次方程 012132 ????? mx)mmx ( ,其根的判别式的值为 1,求m 的值及该方程的解.
四、(本大题共 4 题,共 30 分)
23.(本题满分 8 分,每小题 4 分)
甲乙两辆汽车沿同一公路同时从 A地出发前往相距 90千米的B 地,行驶过程
0 x
y
(A)
0 x
y
(B)
0 x
y
(C)
0 x
y
(D)
y(千米)
x(分钟)60 100
90
甲
乙
o
中所行驶路程分别用 1y 、 2y 表示,它们与行驶与行驶时间 x (单位:分钟)的函数关系如图所示.
(1)填写 1y 关于 x 的函数解析式及定义域___________________________;
填写 2y 关于 x 的函数解析式及定义域___________________________.
(2)分别求行驶了 50 分钟及 80 分钟时,辆车之间相距的路程.
24.(本题满分 8 分,其中第(1)小题 6分,第(2)题 2分)
如图,要建一个面积为 130 平方米的仓库,现有能围成 32 米长的木板,仓库的一边靠墙,并在与墙垂直的一边开
一道 1米宽的小门。
(1)如果墙长 16 米,求仓库的长和宽;
(2)如果墙长a 米,在离开墙 9 米开外仓库一侧修条小路,那么墙长a 米至少要多少米?
25.(本题满分 6 分,第(1)小题 2分,第(2)小题 4 分)
如图,已知点 P 是反比例函数的图像与正比例函数 xy 2?? 的图像的公共点, PQ垂直于 x 轴,垂足Q的坐标为
(2,0).
(1)求这个反比例函数的解析式
(2)如果点M 在这个反比例函数的图像上,且△MPQ的面积为 6,求点M 的坐标.
26. (本题满分 8 分,其中每小题 2分)
已知:如图,正方形 ABCD的边长是 3厘米,动点P 从点B 出发,沿BC 、CD、DA方向运动至点 A点停止.设
点 P 运动的速度为 2 厘米/秒,运动时间为 x 秒, ABP△ 的面积为 y 平方厘米.
小门
小路
y
xo
Q
P
(1)当动点P 在 BC 上运动时,求 y 关于 x 的解析式及定义域;
(2)当动点P 在 DC 上运动时,求 y 关于 x 的解析式及定义域;
(3)当动点P 在 AD 在上运动时,求 y 关于 x 的解析式及定义域;
(3)当 x 取何值时,线段 AP 把正方形的面积分成两部分,且面积比为 2:5?
2018 学年第一学期八年级期中考试
数学试卷参考答案
一、填空题(本大题共 14 题,每题 2 分,满分 28 分)
1. 22 ;2. 2x ?? ;3. ba? ;4. 2 ;5. ba ? 等;6. 32 ??<x ;
7. 01 ?x 22 ?x ;8. )144x)(144x ????( ;9.
7
6
??m ;
10.
3
2
<k ;11.>;12. 223?? ;13.20%;14.0
二、选择题(本大题共 4题,每题 3 分,满分 12 分)
15. A;16. B ;17. D ;18. D .
三、解答题(本大题共 5 题,每题 6 分,满分 30 分)
19. (1)解:原式=
15
6 5 3 5
3
? ? ? ……………4 分(化简一个 1分)
=
15
5 5 3
3
? ? ………………………………1 分
(2)解:原式= 5 4
1
2
a b …………………………………3 分
= 2 2
1
2
a b a ………………………………2分
20.(1)解: 04)3( 2 ???x …………1分
2)3( ???x ………2 分
15 ???? xx 或 ………1分
15 21 ????? xx ,原方程的解是 ………1 分
(2)解:
4
1
2
32 ??? xx ...............1 分
A B
CD
P
A B
CD
A B
CD
16
9
4
1
16
9
2
32 ????? xx .................1 分
16
5
)
4
3
( 2 ??x ................1分
4
5
4
3
???x
4
5
4
3
,
4
5
4
3
21 ???? xx
.................1 分
∴原方程的根
4
5
4
3
,
4
5
4
3
21 ???? xx .................1分
21.解: 3 2 2x ? ? …………………………………1 分
原式=
? ?
2
3 7
3
x
x
? ?
?
………………………………2 分
=
8 7
2 2
?
……………………………………1 分
=
2
4
……………………1 分(也可以直接代入计算)
22.解:由题意得,△=1
又∵△= ? ? )m(m)m( 12413 2 ???? = 122 ?? mm …………………1 分
∴ 12
2 ?? mm =1 解得 20 21 ?? m,m ………………………1分
又∵m ≠0 ∴m =2 …………………………1 分
当m =2 时,原方程为 0352 2 ??? xx ………………………1分
0132 ??? )x)(x( ∴ 1
2
3
21 ?? x,x ……………1 分
所以m 的值为 2,此时原方程的解为 1
2
3
21 ?? x,x
23. 解:(1) xy
2
3
1 ? (0≤ x ≤60)……………2分
xy
10
9
2 ? (0≤ x ≤100)……………2 分
(2)当 50?x 时, 751 ?y , 452 ?y ,这时 75-45=30(千米)……2 分
当 80?x 时,甲车早已到达 B 地, 722 ?y ,这时 90-72=18(千米)……2 分
所以行驶了 50分钟、80分钟时,两车之间相距的路程分别为 30千米、18千米.
24.(1)解:设这个长方形的长为 x米,则宽为
33
2
x?
米……………………1 分
33
130
2
x
x
?
? ? …………………………2 分
1 213, 20x x? ? …………………… 1 分
当
1
20x ? 时,20>16(不合题意,舍去)所以 13x ? ……………1分
这时
33
2
x?
=10
答:这个长方形的长为 13米,宽为 10 米. …………………………1分
(2)当平行于墙的边为 13 米时,垂直于墙的边为 10 米,这时 10>9,所以不合题意,舍去;当平行于墙的边
为 20米时,垂直于墙的边为
2
13
米,这时
2
13
<9,符合题意,所以 20a ? …………………1+1 分
25.(1)由题意可设P (2, y )
因为点P 在正比例函数 xy 2?? 图像上
所以 422 ?????y 所以P (2,-4)…………1 分
设反比例函数的解析式为
x
k
y ? ( k ≠0)
又因为P (2,-4)在反比例函数的图像上
2
4
k
?? k =-8
所以反比例函数的解析式为
x
y
8
?? …………1 分
(2)过点M 作 PQMH ? ,垂足为H
因为 MHPQS MPQ ???
2
1
△ =6,又因为PQ =4,所以MH =3 …………1 分
所以点M 的横坐标为 2+3=5 或 2-3=-1…………1分
因为点M 在反比例函数
x
y
8
?? 上
所以M (5,
5
8
? )或(-1,8)…………2 分
26. (1)当动点P 在 BC 上运动时,BP =2 x , AB =3,
∴ xBPABy 3
2
1
???? (0< x ≤1.5)……………1 分+1 分
(2)当动点P 在 DC 上运动时,过点P 作 PE ⊥ AB 垂足为E ,则PE =3, AB =3
2
9
2
1
???? PEABy (1.5< x ≤3)……………1 分+1 分
(3)当动点P 在 AD 上运动时, AB =3, AP =9-2 x ,
这时
2
)29(3
2
1 x
APABy
?
???? (3< x <4.5)…………1 分+1 分
(4)
7
6
?x 或
7
15
?x …………一个答案 1 分
如答案有误,请自行更正,谢谢.
同课章节目录
