五年级上册数学单元测试-6.多边形的面积(含答案)
文档属性
| 名称 | 五年级上册数学单元测试-6.多边形的面积(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 133.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-30 20:07:18 | ||
图片预览


文档简介
五年级上册数学单元测试-6.多边形的面积
一、单选题
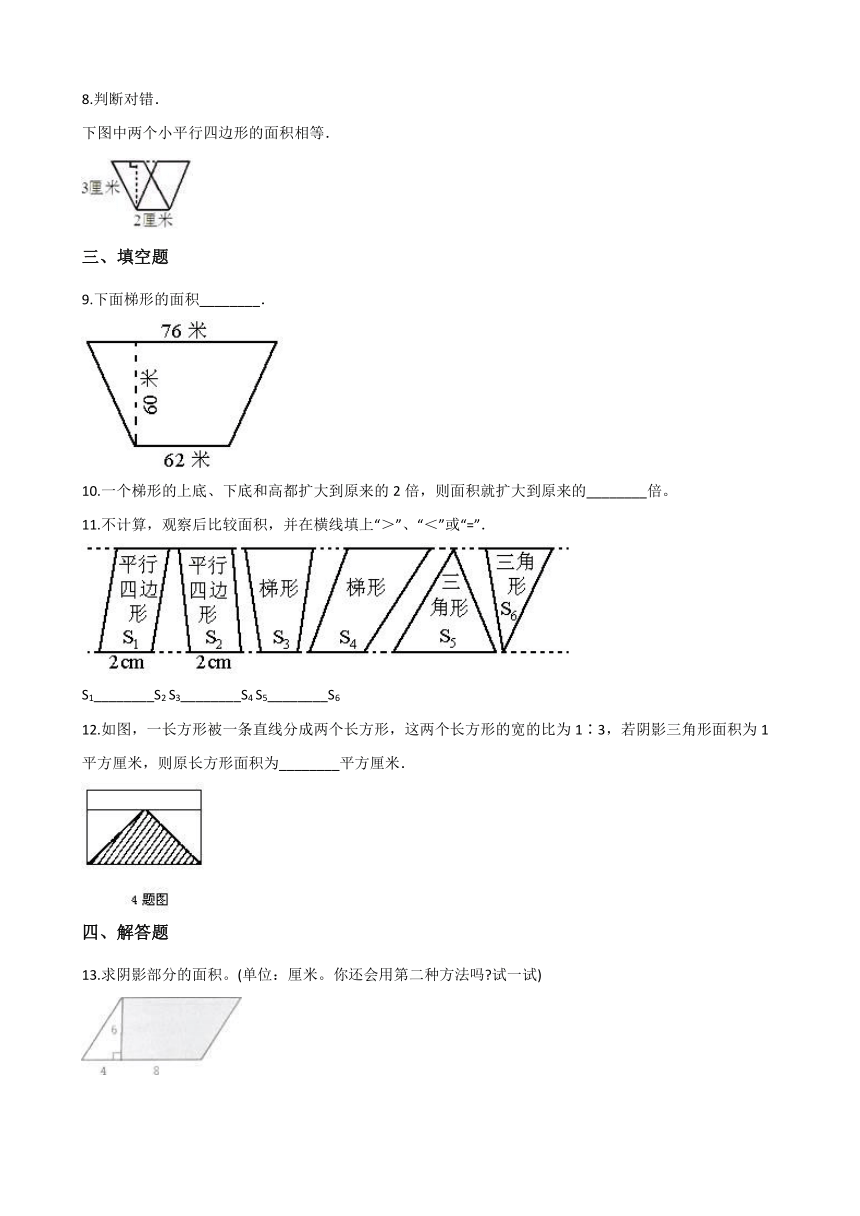
1.三角形的面积是(?? )
A.?53 ????????????????????????????????B.?35 ????????????????????????????????C.?30 ????????????????????????????????D.?70
2.如图中,一组平行线间有甲乙丙三个图形,其中面积最大的是(?? )
A.?甲?????????????????????????????????????????????B.?乙?????????????????????????????????????????????C.?丙
3.一个梯形的面积是18m2 , 它的上底是3m,高是4m,求它的下底。下面(??? )是正确的。
A.?18÷4-3=1.5????????????????????B.?18×2÷4-3=6????????????????????C.?18×2÷4+3=12????????????????????D.?无法计算
4.如下图,AB与CD平行,E是AB的中点,比较三角形甲和三角形乙的面积,结果是(?? )
A.?甲面积大????????????????????????????????B.?乙面积大????????????????????????????????C.?它们面积相等
二、判断题
5.三角形的底越长,面积就越大。
6.底乘以另一条底上的高也可以求出平行四边形的面积。
7.判断,正确的填“正确”,错误的填“错误”.
三角形的底是8cm,高是4cm,面积是32 .
8.判断对错. 下图中两个小平行四边形的面积相等.
三、填空题
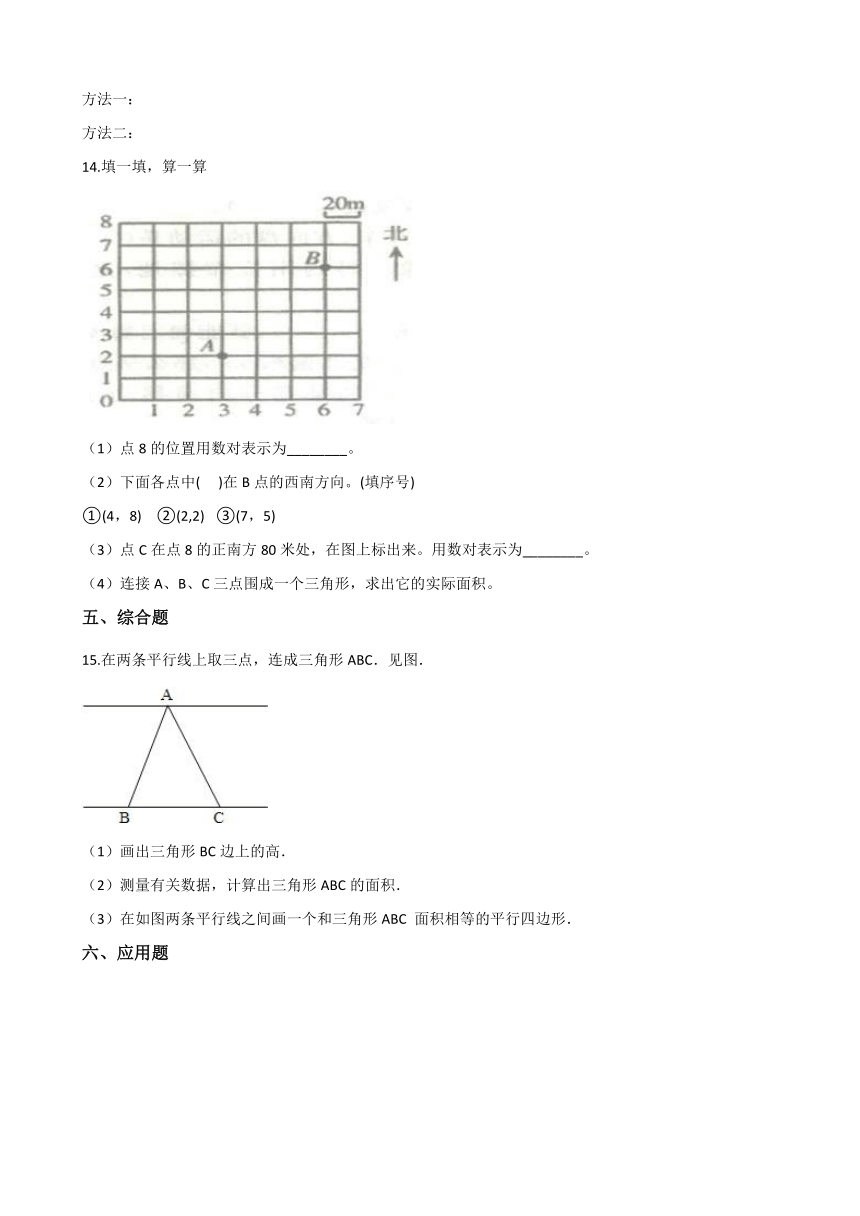
9.下面梯形的面积________.
10.一个梯形的上底、下底和高都扩大到原来的2倍,则面积就扩大到原来的________倍。
11.不计算,观察后比较面积,并在横线填上“>”、“<”或“=”.
S1________S2
S3________S4
S5________S6
12.如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1∶3,若阴影三角形面积为1平方厘米,则原长方形面积为________平方厘米.
四、解答题
13.求阴影部分的面积。(单位:厘米。你还会用第二种方法吗?试一试) 方法一: 方法二:
14.填一填,算一算
(1)点8的位置用数对表示为________。
(2)下面各点中(??? )在B点的西南方向。(填序号)
①(4,8) ??②(2,2)? ③(7,5)
(3)点C在点8的正南方80米处,在图上标出来。用数对表示为________。
(4)连接A、B、C三点围成一个三角形,求出它的实际面积。
五、综合题
15.在两条平行线上取三点,连成三角形ABC.见图.
(1)画出三角形BC边上的高.
(2)测量有关数据,计算出三角形ABC的面积.
(3)在如图两条平行线之间画一个和三角形ABC 面积相等的平行四边形.
六、应用题
16.已知:ABCD是长方形,DC=4cm,AD=6cm,E是DF的中点,求S△EFC?
17.如图,长方形里画了两个同样的半圆,求阴影部分面积.
参考答案
一、单选题
1.【答案】 B
【解析】【解答】10 × 7 ÷ 2=35
【分析】三角形的面积=对应的底对应的高2=1072=35
2.【答案】 B
【解析】【解答】解:设高是h, 甲:12×h÷2=6h; 乙:7×h=7h; 丙:(3+8)×h÷2=5.5h; 所以面积最大的是乙。 故答案为:B。 【分析】三个图形的高相等,三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,设出高,分别表示出三个图形的面积并判断面积的大小即可。
3.【答案】 B
【解析】【解答】解:梯形的下底是:18×2÷4-3=6。 故答案为:B。
【分析】由梯形的面积公式:梯形的面积=(上底+下底)×高÷2,可以得到梯形的下底=梯形的面积×2÷高-上底
4.【答案】 C
【解析】【解答】三角形甲的面积为:AC×AE÷2,三角形乙的面积为:BD×BE÷2,因为AC=BD,AE=BE,所以三角形甲的面积=三角形乙的面积. 故答案为:C.
【分析】因为E是AB的中点,所以AE=BE,长方形对边相等AC=BD,再根据三角形甲的面积=AC×AE÷2,三角形乙的面积=BD×BE÷2即可得出答案.
二、判断题
5.【答案】错误
【解析】【解答】当三角形的高不变时,三角形的底越长,面积就越大,原题说法错误. 故答案为:错误.【分析】因为三角形的面积=底×高÷2,决定三角形面积大小的因素有两个,那就是它的底和对应底上的高,据此判断.
6.【答案】错误
【解析】【解答】解:底乘以这条底对应的高可以求出平行四边形的面积,原题说法错误。 故答案为:错误【分析】平行四边形面积=底×高,注意底和高一定是对应的。
7.【答案】错误
【解析】【解答】解答:三角形的底是8cm,高是4cm,面积是16 .
运用“底×高”计算三角形的面积是不对的.
【分析】三角形的面积=底×高÷2.
8.【答案】正确
【解析】【解答】这两个平行四边的底都是2厘米,高都是3厘米,面积是相等的,原题说法正确. 故答案为:正确 【分析】平行四边形面积=底×高,注意等底等高的平行四边形面积是相等的.
三、填空题
9.【答案】4140平方米
【解析】【解答】解:(76+62)×60÷2 =138×60÷2 =4140(平方米) 故答案为:4140平方米 【分析】本题考查的主要内容是梯形的面积计算问题,根据梯形的面积公式进行分析即可.
10.【答案】4
【解析】【解答】一个梯形的上底、下底和高都扩大到原来的2倍,则面积就扩大到原来的4倍. 故答案为:4.【分析】根据梯形的面积=(上底+下底)×高÷2,梯形的上底扩大到原来的2倍,下底也扩大2倍,则(上底+下底)的和扩大了2倍,高扩大2倍,它的面积将扩大到原来的2×2=4倍,据此解答.
11.【答案】=;<;>
【解析】【解答】S1=S2,S3<S4 , S5>S6。 【分析】两个平行四边形的底和高的长度都是相等,所以两个平行四边形的面积相等;两个梯形的高相等,但是第一个图形的上底和下底的长度都不如第二个图形的上底和下底的长度长,所以第一个图形的面积没有第二个图形的面积大;两个三角形的高是相等的,但第一个三角形的底比第二个三角形的底长,所以第一个三角形的面积大于第二个三角形的面积。
12.【答案】
【解析】【解答】解:阴影三角形的高=长方形的宽,阴影三角形的面积=长方形的长×高÷2=长方形的长×长方形的宽÷2=1,即长方形的长×长方形的宽=(平方厘米). 故答案为:.
【分析】由两个长方形的宽的比为1∶3可以推出阴影三角形的高=长方形的宽,再根据阴影三角形的面积是1推出长方形的长与宽的积,进而求得原来长方形的面积.
四、解答题
13.【答案】解:方法一: (4+8)×6-4×6÷2 =12×6-24÷2 =72-12 =60(平方厘米) 方法二: (8+4+8)×6÷2 =20×6÷2 =60(平方厘米) 答:阴影部分的面积是60平方厘米.
【解析】【分析】方法一:用平行四边形的面积减去空白部分三角形的面积就是阴影部分的面积;方法二:直接根据梯形的面积来计算阴影部分的面积即可.
14.【答案】 (1)(6,6) (2)解:② (3)解:图略? (6,2) (4)解:(3×20×4×20)÷2=2400(平方米)
【解析】【解答】解:(1)点B的位置用数对表示为(6,6); (2)①是在B点的正西方向,②是在B点的西南方向,③是在B点的东南方向; (3)80÷20=4,点C用数对表示为(6,2); 故答案为:(1)(6,6);(2)②;(3)(6,2)。 【分析】(1)数对中第一个数表示列,第二个数表示行;根据B点所在的列与行用数对表示; (2)确定每个点的位置后,再根据图上的方向判断即可; (3)80米是图上的4格,先确定C点的位置再用数对表示; (4)围成的图形是一个直角三角形,用图上的距离乘20求出实际距离,用实际的底乘高再除以2即可求出实际面积。
五、综合题
15.【答案】(1)解:如图,画出三角形ABC的BC边上的高AD
(2)解:经过测量可得:BC=2厘米,AD=3厘米,则三角形的面积是:2×3÷2=3(平方厘米)
(3)解:根据平行四边形和三角形的面积公式可以画出与它面积相等的平行四边形如下
【解析】【分析】(1)从A点向BC边作垂线,点A到对边垂足之间的线段,是这个三角形的一条高;(2)三角形的面积=底×高÷2,据此测量出BC与AD的长度即可计算出这个三角形的面积;③三角形的面积是与其等底等高的平行四边形面积的一半,所以所画的平行四边形的底只要等于三角形的底的一半即可.本题考查了学生三角形高的作法,以及三角形的面积公式与平行四边形的面积公式的计算方法的灵活应用.
六、应用题
16.【答案】解:因为AF∥DC,所以三角形DCE∽三角形FBE,CE:BE=DE:FE,由于E是DF的中点,所以E也是DF的中点, 三角形DCE的面积:4×(6÷2)÷2 =4×3÷2 =6(cm2) 三角形DCF的面积:4×6÷2=12(cm2) 三角形EFC的面积:12﹣6=6(cm2) 答:三角形EFC的面积6cm2
【解析】【分析】阴影三有形面积等于三角形DCF的面积减去三角形DCE的面积.三角形DCF的底与长方形的宽相等,高与长方形的长相等,长方形的长、宽已知,三角形FDC的面积可求;因为AF∥DC,所以三角形DCE∽三角形FBE,CE:BE=DE:FE,由于E是DF的中点,所以E也是DF的中点,三角形DCE的底等于长方形的宽,高为长方形长的一半,面积可求.
17.【答案】解:20×10﹣3.14×(10÷2)2 , =200﹣78.5, =121.5(平方厘米); 答:阴影部分的面积是121.5平方厘米
【解析】【分析】由图意可知:阴影部分的面积=长方形的面积﹣圆的面积,又因圆的直径等于长方形的宽,于是利用长方形和圆的面积公式即可求解.解答此题的关键是明白:阴影部分的面积可以由哪些图形的面积和或差求出.
一、单选题
1.三角形的面积是(?? )
A.?53 ????????????????????????????????B.?35 ????????????????????????????????C.?30 ????????????????????????????????D.?70
2.如图中,一组平行线间有甲乙丙三个图形,其中面积最大的是(?? )
A.?甲?????????????????????????????????????????????B.?乙?????????????????????????????????????????????C.?丙
3.一个梯形的面积是18m2 , 它的上底是3m,高是4m,求它的下底。下面(??? )是正确的。
A.?18÷4-3=1.5????????????????????B.?18×2÷4-3=6????????????????????C.?18×2÷4+3=12????????????????????D.?无法计算
4.如下图,AB与CD平行,E是AB的中点,比较三角形甲和三角形乙的面积,结果是(?? )
A.?甲面积大????????????????????????????????B.?乙面积大????????????????????????????????C.?它们面积相等
二、判断题
5.三角形的底越长,面积就越大。
6.底乘以另一条底上的高也可以求出平行四边形的面积。
7.判断,正确的填“正确”,错误的填“错误”.
三角形的底是8cm,高是4cm,面积是32 .
8.判断对错. 下图中两个小平行四边形的面积相等.
三、填空题
9.下面梯形的面积________.
10.一个梯形的上底、下底和高都扩大到原来的2倍,则面积就扩大到原来的________倍。
11.不计算,观察后比较面积,并在横线填上“>”、“<”或“=”.
S1________S2
S3________S4
S5________S6
12.如图,一长方形被一条直线分成两个长方形,这两个长方形的宽的比为1∶3,若阴影三角形面积为1平方厘米,则原长方形面积为________平方厘米.
四、解答题
13.求阴影部分的面积。(单位:厘米。你还会用第二种方法吗?试一试) 方法一: 方法二:
14.填一填,算一算
(1)点8的位置用数对表示为________。
(2)下面各点中(??? )在B点的西南方向。(填序号)
①(4,8) ??②(2,2)? ③(7,5)
(3)点C在点8的正南方80米处,在图上标出来。用数对表示为________。
(4)连接A、B、C三点围成一个三角形,求出它的实际面积。
五、综合题
15.在两条平行线上取三点,连成三角形ABC.见图.
(1)画出三角形BC边上的高.
(2)测量有关数据,计算出三角形ABC的面积.
(3)在如图两条平行线之间画一个和三角形ABC 面积相等的平行四边形.
六、应用题
16.已知:ABCD是长方形,DC=4cm,AD=6cm,E是DF的中点,求S△EFC?
17.如图,长方形里画了两个同样的半圆,求阴影部分面积.
参考答案
一、单选题
1.【答案】 B
【解析】【解答】10 × 7 ÷ 2=35
【分析】三角形的面积=对应的底对应的高2=1072=35
2.【答案】 B
【解析】【解答】解:设高是h, 甲:12×h÷2=6h; 乙:7×h=7h; 丙:(3+8)×h÷2=5.5h; 所以面积最大的是乙。 故答案为:B。 【分析】三个图形的高相等,三角形面积=底×高÷2,平行四边形面积=底×高,梯形面积=(上底+下底)×高÷2,设出高,分别表示出三个图形的面积并判断面积的大小即可。
3.【答案】 B
【解析】【解答】解:梯形的下底是:18×2÷4-3=6。 故答案为:B。
【分析】由梯形的面积公式:梯形的面积=(上底+下底)×高÷2,可以得到梯形的下底=梯形的面积×2÷高-上底
4.【答案】 C
【解析】【解答】三角形甲的面积为:AC×AE÷2,三角形乙的面积为:BD×BE÷2,因为AC=BD,AE=BE,所以三角形甲的面积=三角形乙的面积. 故答案为:C.
【分析】因为E是AB的中点,所以AE=BE,长方形对边相等AC=BD,再根据三角形甲的面积=AC×AE÷2,三角形乙的面积=BD×BE÷2即可得出答案.
二、判断题
5.【答案】错误
【解析】【解答】当三角形的高不变时,三角形的底越长,面积就越大,原题说法错误. 故答案为:错误.【分析】因为三角形的面积=底×高÷2,决定三角形面积大小的因素有两个,那就是它的底和对应底上的高,据此判断.
6.【答案】错误
【解析】【解答】解:底乘以这条底对应的高可以求出平行四边形的面积,原题说法错误。 故答案为:错误【分析】平行四边形面积=底×高,注意底和高一定是对应的。
7.【答案】错误
【解析】【解答】解答:三角形的底是8cm,高是4cm,面积是16 .
运用“底×高”计算三角形的面积是不对的.
【分析】三角形的面积=底×高÷2.
8.【答案】正确
【解析】【解答】这两个平行四边的底都是2厘米,高都是3厘米,面积是相等的,原题说法正确. 故答案为:正确 【分析】平行四边形面积=底×高,注意等底等高的平行四边形面积是相等的.
三、填空题
9.【答案】4140平方米
【解析】【解答】解:(76+62)×60÷2 =138×60÷2 =4140(平方米) 故答案为:4140平方米 【分析】本题考查的主要内容是梯形的面积计算问题,根据梯形的面积公式进行分析即可.
10.【答案】4
【解析】【解答】一个梯形的上底、下底和高都扩大到原来的2倍,则面积就扩大到原来的4倍. 故答案为:4.【分析】根据梯形的面积=(上底+下底)×高÷2,梯形的上底扩大到原来的2倍,下底也扩大2倍,则(上底+下底)的和扩大了2倍,高扩大2倍,它的面积将扩大到原来的2×2=4倍,据此解答.
11.【答案】=;<;>
【解析】【解答】S1=S2,S3<S4 , S5>S6。 【分析】两个平行四边形的底和高的长度都是相等,所以两个平行四边形的面积相等;两个梯形的高相等,但是第一个图形的上底和下底的长度都不如第二个图形的上底和下底的长度长,所以第一个图形的面积没有第二个图形的面积大;两个三角形的高是相等的,但第一个三角形的底比第二个三角形的底长,所以第一个三角形的面积大于第二个三角形的面积。
12.【答案】
【解析】【解答】解:阴影三角形的高=长方形的宽,阴影三角形的面积=长方形的长×高÷2=长方形的长×长方形的宽÷2=1,即长方形的长×长方形的宽=(平方厘米). 故答案为:.
【分析】由两个长方形的宽的比为1∶3可以推出阴影三角形的高=长方形的宽,再根据阴影三角形的面积是1推出长方形的长与宽的积,进而求得原来长方形的面积.
四、解答题
13.【答案】解:方法一: (4+8)×6-4×6÷2 =12×6-24÷2 =72-12 =60(平方厘米) 方法二: (8+4+8)×6÷2 =20×6÷2 =60(平方厘米) 答:阴影部分的面积是60平方厘米.
【解析】【分析】方法一:用平行四边形的面积减去空白部分三角形的面积就是阴影部分的面积;方法二:直接根据梯形的面积来计算阴影部分的面积即可.
14.【答案】 (1)(6,6) (2)解:② (3)解:图略? (6,2) (4)解:(3×20×4×20)÷2=2400(平方米)
【解析】【解答】解:(1)点B的位置用数对表示为(6,6); (2)①是在B点的正西方向,②是在B点的西南方向,③是在B点的东南方向; (3)80÷20=4,点C用数对表示为(6,2); 故答案为:(1)(6,6);(2)②;(3)(6,2)。 【分析】(1)数对中第一个数表示列,第二个数表示行;根据B点所在的列与行用数对表示; (2)确定每个点的位置后,再根据图上的方向判断即可; (3)80米是图上的4格,先确定C点的位置再用数对表示; (4)围成的图形是一个直角三角形,用图上的距离乘20求出实际距离,用实际的底乘高再除以2即可求出实际面积。
五、综合题
15.【答案】(1)解:如图,画出三角形ABC的BC边上的高AD
(2)解:经过测量可得:BC=2厘米,AD=3厘米,则三角形的面积是:2×3÷2=3(平方厘米)
(3)解:根据平行四边形和三角形的面积公式可以画出与它面积相等的平行四边形如下
【解析】【分析】(1)从A点向BC边作垂线,点A到对边垂足之间的线段,是这个三角形的一条高;(2)三角形的面积=底×高÷2,据此测量出BC与AD的长度即可计算出这个三角形的面积;③三角形的面积是与其等底等高的平行四边形面积的一半,所以所画的平行四边形的底只要等于三角形的底的一半即可.本题考查了学生三角形高的作法,以及三角形的面积公式与平行四边形的面积公式的计算方法的灵活应用.
六、应用题
16.【答案】解:因为AF∥DC,所以三角形DCE∽三角形FBE,CE:BE=DE:FE,由于E是DF的中点,所以E也是DF的中点, 三角形DCE的面积:4×(6÷2)÷2 =4×3÷2 =6(cm2) 三角形DCF的面积:4×6÷2=12(cm2) 三角形EFC的面积:12﹣6=6(cm2) 答:三角形EFC的面积6cm2
【解析】【分析】阴影三有形面积等于三角形DCF的面积减去三角形DCE的面积.三角形DCF的底与长方形的宽相等,高与长方形的长相等,长方形的长、宽已知,三角形FDC的面积可求;因为AF∥DC,所以三角形DCE∽三角形FBE,CE:BE=DE:FE,由于E是DF的中点,所以E也是DF的中点,三角形DCE的底等于长方形的宽,高为长方形长的一半,面积可求.
17.【答案】解:20×10﹣3.14×(10÷2)2 , =200﹣78.5, =121.5(平方厘米); 答:阴影部分的面积是121.5平方厘米
【解析】【分析】由图意可知:阴影部分的面积=长方形的面积﹣圆的面积,又因圆的直径等于长方形的宽,于是利用长方形和圆的面积公式即可求解.解答此题的关键是明白:阴影部分的面积可以由哪些图形的面积和或差求出.
