初中数学北师大版 第三章 位置与坐标 单元测试卷 (解析版)
文档属性
| 名称 | 初中数学北师大版 第三章 位置与坐标 单元测试卷 (解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-30 17:19:56 | ||
图片预览


文档简介
初中数学北师大版八年级上学期 第三章测试卷
一、单选题
1.根据下列表述,能确定具体位置的是(?? )
A.?我校八年级(1)班班级座位3排4列???????B.?滨海县育才路 ???????C.?东经118°???????D.?县一中北偏东60°
2.平面直角坐标系中,点A(-3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的长度最小时点C的坐标为(?? ) 21教育网
A.?(-3,4)????????????????????????????????B.?(3,2)????????????????????????????????C.?(3,0)????????????????????????????????D.?(4,2)
3.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是(? ?)
A.?(66,34)?????????????????????B.?(67,33)?????????????????????C.?(100,33)?????????????????????D.?(99,34)
4.点P(m+3、m+1)在x轴上,则P点的坐标为( ??)
A.?(0,1)??????????????????????????B.?(1,0)??????????????????????????C.?(0,-2)??????????????????????????D.?(2,0)
二、填空题
5.如果将电影票上“8排5号”简记为(8,5),那么“11排11号”可表示为________ ;(5,6)表示的含义是________ . 21·cn·jy·com
6.平面直角坐标系的应用十分广泛,用坐标表示地理位置体现了坐标系在实际生活中的应用.不管是出差办事,还是出去旅游,人民都愿意带上一副地图,它给人们出行带来了很大方便.如图是某市地图的一部分.在图中,分别以正东、正北方向为 轴, 轴的正方向建立平面直角坐标系,若表示牡丹园的点的坐标为 ,则表示狮虎园的点的坐标为________. 21·世纪*教育网
7.如图,一所学校的平面示意图中,如果图书馆的位置记作(3,2),实验楼的位置记作(1,﹣1),则校门的位置记作________. 2-1-c-n-j-y
8.如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点C的坐标是________. www.21-cn-jy.com
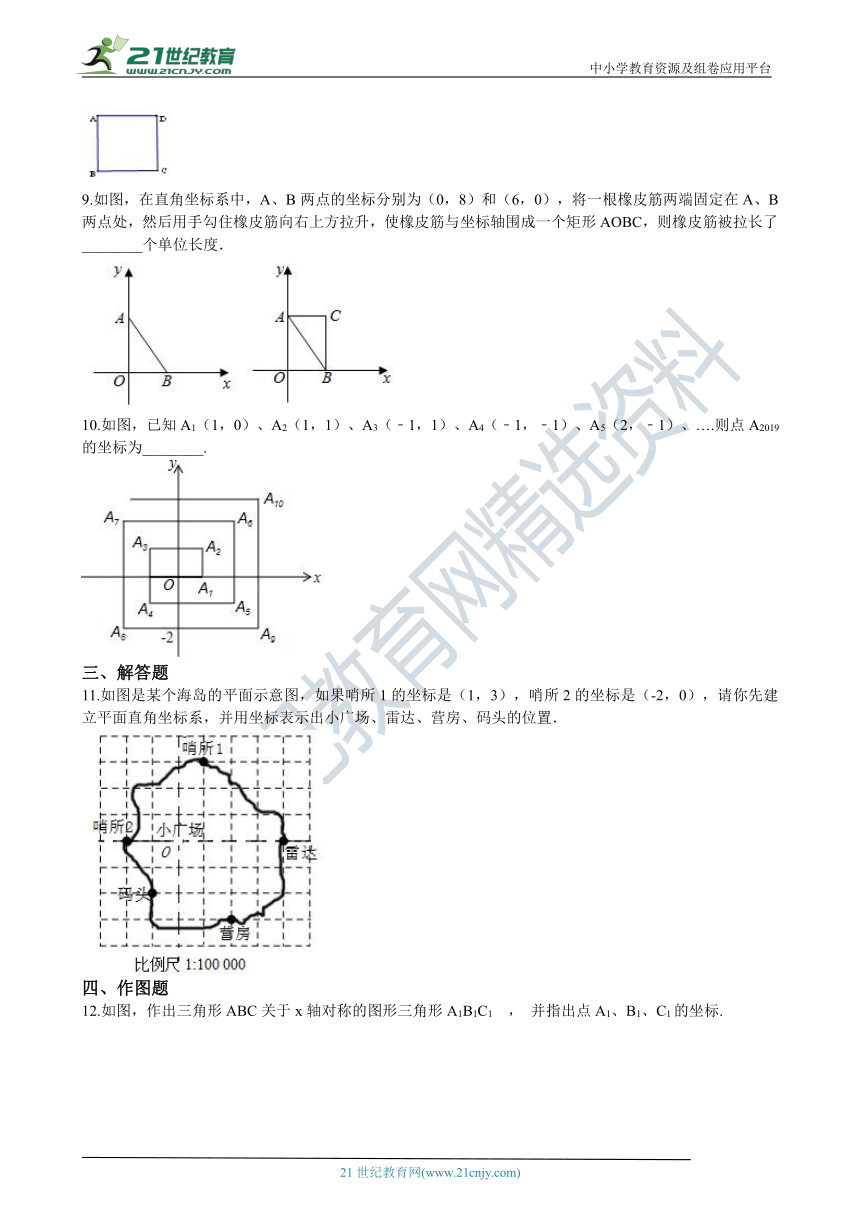
9.如图,在直角坐标系中,A、B两点的坐标分别为(0,8)和(6,0),将一根橡皮筋两端固定在A、B两点处,然后用手勾住橡皮筋向右上方拉升,使橡皮筋与坐标轴围成一个矩形AOBC,则橡皮筋被拉长了________个单位长度. 21*cnjy*com
10.如图,已知A1(1,0)、A2(1,1)、A3(﹣1,1)、A4(﹣1,﹣1)、A5(2,﹣1)、….则点A2019的坐标为________. 【出处:21教育名师】
三、解答题
11.如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置. 【版权所有:21教育】
四、作图题
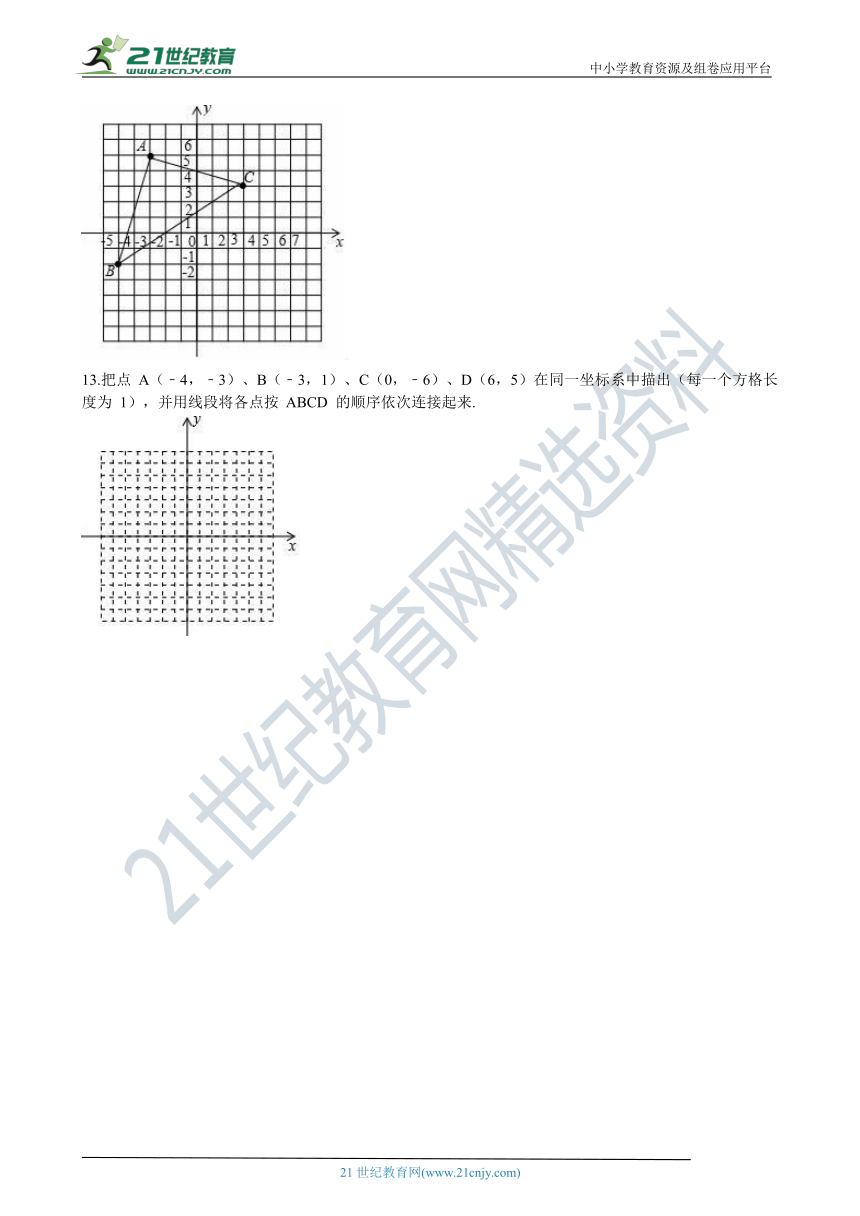
12.如图,作出三角形ABC关于x轴对称的图形三角形A1B1C1 , 并指出点A1、B1、C1的坐标.
13.把点 A(﹣4,﹣3)、B(﹣3,1)、C(0,﹣6)、D(6,5)在同一坐标系中描出(每一个方格长度为 1),并用线段将各点按 ABCD 的顺序依次连接起来. 21教育名师原创作品
答案解析部分
一、单选题
1. A
解:A.我校八年级(1)班班级座位3排4列,能确定具体位置,故符合题意;
B.滨海县育才路,不能确定具体位置,故不符合题意;
C.东经118°,不能确定具体位置,故不符合题意;
D.县一中北偏东60°,不能确定具体位置,故不符合题意.
故答案为:A.
【分析】根据用点的坐标确定地理位置是用一对有序实数对表示,由此可排除B,C,D,即可得到答案。
2. B
解:∵AC∥x轴, ∴A、C点纵坐标相同,即yC=2, BC的长度最小,只有当BC⊥AC时,即BC⊥x轴, 这时B、C的横坐标相同,即xC=xB=3, ∴C点坐标为(3,2); 故答案为:B. 【来源:21cnj*y.co*m】
【分析】根据AC∥x轴,得到A、C点纵坐标相同,由于BC的长度最小,只有当BC⊥AC时,即BC⊥x轴, 得到B、C的横坐标相同,据此求出C点坐标。
3. C
由题意得,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,
∵100÷3=33余1,
∴走完第100步,为第34个循环组的第1步,
所处位置的横坐标为33×3+1=100,
纵坐标为33×1=33,
∴棋子所处位置的坐标是(100,33).
故答案为:C.
【分析】根据题意可知规律为:每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,用100÷3,可得余数为1,据此可求出棋子所处位置的横纵坐标,即可求解。
4. D
∵点P(m+3,m+1)在直角坐标系的x轴上,
∴m+1=0,
解得m=?1,
所以,m+3=?1+3=2,
所以,点P的坐标为(2,0).
故答案为::D.
【分析】根据x轴的坐标规律,x轴上的点纵坐标为0,可得m+1=0,求出m即可解答.
二、填空题
5. (11,11);5排6号
“11排11号”可表示为(11,11);(5,6)表示的含义是5排6号
【分析】根据题意,可用坐标表示地理位置。
6.
解:如图画出平面直角坐标系:
表示狮虎园的点的坐标为:(6,-2).
故答案为:(6,-2) 【分析】根据题意,找到狮虎园的坐标即可得到答案。
7. (﹣2,0)
解:建立坐标系如图所示,由图象可知,校门的位置记作(﹣2,0).故答案为:(﹣2,0). 21世纪教育网版权所有
【分析】以实验楼的坐标(1,-1)为基础,分别向左和向上平移一个单位所在的位置作为原点的位置,建立平面直角坐标系,再根据校门所在的位置即可写出校门的坐标。21cnjy.com
8. (3,0)
∵ 正方形ABCD的顶点B、C都在直角坐标系的x轴上,点A的坐标是(-1,4) ∴BC=AB=4,B(-1,0) 2·1·c·n·j·y
∴点C的坐标是(3,0). 【分析】根据点A的坐标即可确定正方形的边长及点B的坐标,从而求得点C的坐标.
9. 4
解:?, AC+BC=OB+OA=6+8=14; ∴拉长的距离=14-10=4; 【分析】由勾股定理求出AB,即橡皮筋的原长,橡皮筋拉伸后的长度为AC和BC之和,拉伸后的长度减原长即是被拉长的长度。www-2-1-cnjy-com
10. (-505,505)
解:观察图形,可知:点A3的坐标为(﹣1,1),点A7的坐标为(﹣2,2),点A11的坐标为(﹣3,3),…, 21*cnjy*com
∴点A4n﹣1的坐标为(﹣n,n)(n为正整数).
又∵2019=4×505﹣1,
∴点A2019的坐标为(﹣505,505).
故答案为:(﹣505,505).
【分析】观察图形可知,根据(A1和第四象限的点除外)各个点分别位于象限的角平分线上,分别探究出各个象限 的点的坐标特点,可知点A4n﹣1的坐标为(﹣n,n)(n为正整数),再根据2019=4×505﹣1,就可得到点A2019的坐标。【来源:21·世纪·教育·网】
三、解答题
11. 解:建立如图所示的平面直角坐标系:
小广场(0,0)、雷达(4,0)、营房(2,-3)、码头(-1,-2)
【分析】利用直角坐标系中的坐标的表示方法,可依次表示出四个地点的坐标。
四、作图题
12. 解:如图所示:△A1B1C1 , 即为所求,
A1(﹣3,﹣5);B1(﹣5,2);C1(3,﹣2).
【分析】利用方格纸的特点及轴对称的性质,分别作出点A、B、C关于x轴的对称点 A1、B1、C1 , 再首尾顺次相连即可得出所求的△ A1B1C1;结合图形即可写出点 A1、B1、C1的坐标。
13. 解:如图所示:
【分析】利用方格纸的特点及点的坐标与象限的关系即可分别描出各个点,再用线段按要求连接起来。
一、单选题
1.根据下列表述,能确定具体位置的是(?? )
A.?我校八年级(1)班班级座位3排4列???????B.?滨海县育才路 ???????C.?东经118°???????D.?县一中北偏东60°
2.平面直角坐标系中,点A(-3,2),B(3,4),C(x,y),若AC∥x轴,则线段BC的长度最小时点C的坐标为(?? ) 21教育网
A.?(-3,4)????????????????????????????????B.?(3,2)????????????????????????????????C.?(3,0)????????????????????????????????D.?(4,2)
3.在平面直角坐标系中,孔明做走棋的游戏,其走法是:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…依此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n被3除,余数为1时,则向右走1个单位;当n被3除,余数为2时,则向右走2个单位,当走完第100步时,棋子所处位置的坐标是(? ?)
A.?(66,34)?????????????????????B.?(67,33)?????????????????????C.?(100,33)?????????????????????D.?(99,34)
4.点P(m+3、m+1)在x轴上,则P点的坐标为( ??)
A.?(0,1)??????????????????????????B.?(1,0)??????????????????????????C.?(0,-2)??????????????????????????D.?(2,0)
二、填空题
5.如果将电影票上“8排5号”简记为(8,5),那么“11排11号”可表示为________ ;(5,6)表示的含义是________ . 21·cn·jy·com
6.平面直角坐标系的应用十分广泛,用坐标表示地理位置体现了坐标系在实际生活中的应用.不管是出差办事,还是出去旅游,人民都愿意带上一副地图,它给人们出行带来了很大方便.如图是某市地图的一部分.在图中,分别以正东、正北方向为 轴, 轴的正方向建立平面直角坐标系,若表示牡丹园的点的坐标为 ,则表示狮虎园的点的坐标为________. 21·世纪*教育网
7.如图,一所学校的平面示意图中,如果图书馆的位置记作(3,2),实验楼的位置记作(1,﹣1),则校门的位置记作________. 2-1-c-n-j-y
8.如图,正方形ABCD的顶点B、C都在直角坐标系的x轴上,若点A的坐标是(-1,4),则点C的坐标是________. www.21-cn-jy.com
9.如图,在直角坐标系中,A、B两点的坐标分别为(0,8)和(6,0),将一根橡皮筋两端固定在A、B两点处,然后用手勾住橡皮筋向右上方拉升,使橡皮筋与坐标轴围成一个矩形AOBC,则橡皮筋被拉长了________个单位长度. 21*cnjy*com
10.如图,已知A1(1,0)、A2(1,1)、A3(﹣1,1)、A4(﹣1,﹣1)、A5(2,﹣1)、….则点A2019的坐标为________. 【出处:21教育名师】
三、解答题
11.如图是某个海岛的平面示意图,如果哨所1的坐标是(1,3),哨所2的坐标是(-2,0),请你先建立平面直角坐标系,并用坐标表示出小广场、雷达、营房、码头的位置. 【版权所有:21教育】
四、作图题
12.如图,作出三角形ABC关于x轴对称的图形三角形A1B1C1 , 并指出点A1、B1、C1的坐标.
13.把点 A(﹣4,﹣3)、B(﹣3,1)、C(0,﹣6)、D(6,5)在同一坐标系中描出(每一个方格长度为 1),并用线段将各点按 ABCD 的顺序依次连接起来. 21教育名师原创作品
答案解析部分
一、单选题
1. A
解:A.我校八年级(1)班班级座位3排4列,能确定具体位置,故符合题意;
B.滨海县育才路,不能确定具体位置,故不符合题意;
C.东经118°,不能确定具体位置,故不符合题意;
D.县一中北偏东60°,不能确定具体位置,故不符合题意.
故答案为:A.
【分析】根据用点的坐标确定地理位置是用一对有序实数对表示,由此可排除B,C,D,即可得到答案。
2. B
解:∵AC∥x轴, ∴A、C点纵坐标相同,即yC=2, BC的长度最小,只有当BC⊥AC时,即BC⊥x轴, 这时B、C的横坐标相同,即xC=xB=3, ∴C点坐标为(3,2); 故答案为:B. 【来源:21cnj*y.co*m】
【分析】根据AC∥x轴,得到A、C点纵坐标相同,由于BC的长度最小,只有当BC⊥AC时,即BC⊥x轴, 得到B、C的横坐标相同,据此求出C点坐标。
3. C
由题意得,每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,
∵100÷3=33余1,
∴走完第100步,为第34个循环组的第1步,
所处位置的横坐标为33×3+1=100,
纵坐标为33×1=33,
∴棋子所处位置的坐标是(100,33).
故答案为:C.
【分析】根据题意可知规律为:每3步为一个循环组依次循环,且一个循环组内向右3个单位,向上1个单位,用100÷3,可得余数为1,据此可求出棋子所处位置的横纵坐标,即可求解。
4. D
∵点P(m+3,m+1)在直角坐标系的x轴上,
∴m+1=0,
解得m=?1,
所以,m+3=?1+3=2,
所以,点P的坐标为(2,0).
故答案为::D.
【分析】根据x轴的坐标规律,x轴上的点纵坐标为0,可得m+1=0,求出m即可解答.
二、填空题
5. (11,11);5排6号
“11排11号”可表示为(11,11);(5,6)表示的含义是5排6号
【分析】根据题意,可用坐标表示地理位置。
6.
解:如图画出平面直角坐标系:
表示狮虎园的点的坐标为:(6,-2).
故答案为:(6,-2) 【分析】根据题意,找到狮虎园的坐标即可得到答案。
7. (﹣2,0)
解:建立坐标系如图所示,由图象可知,校门的位置记作(﹣2,0).故答案为:(﹣2,0). 21世纪教育网版权所有
【分析】以实验楼的坐标(1,-1)为基础,分别向左和向上平移一个单位所在的位置作为原点的位置,建立平面直角坐标系,再根据校门所在的位置即可写出校门的坐标。21cnjy.com
8. (3,0)
∵ 正方形ABCD的顶点B、C都在直角坐标系的x轴上,点A的坐标是(-1,4) ∴BC=AB=4,B(-1,0) 2·1·c·n·j·y
∴点C的坐标是(3,0). 【分析】根据点A的坐标即可确定正方形的边长及点B的坐标,从而求得点C的坐标.
9. 4
解:?, AC+BC=OB+OA=6+8=14; ∴拉长的距离=14-10=4; 【分析】由勾股定理求出AB,即橡皮筋的原长,橡皮筋拉伸后的长度为AC和BC之和,拉伸后的长度减原长即是被拉长的长度。www-2-1-cnjy-com
10. (-505,505)
解:观察图形,可知:点A3的坐标为(﹣1,1),点A7的坐标为(﹣2,2),点A11的坐标为(﹣3,3),…, 21*cnjy*com
∴点A4n﹣1的坐标为(﹣n,n)(n为正整数).
又∵2019=4×505﹣1,
∴点A2019的坐标为(﹣505,505).
故答案为:(﹣505,505).
【分析】观察图形可知,根据(A1和第四象限的点除外)各个点分别位于象限的角平分线上,分别探究出各个象限 的点的坐标特点,可知点A4n﹣1的坐标为(﹣n,n)(n为正整数),再根据2019=4×505﹣1,就可得到点A2019的坐标。【来源:21·世纪·教育·网】
三、解答题
11. 解:建立如图所示的平面直角坐标系:
小广场(0,0)、雷达(4,0)、营房(2,-3)、码头(-1,-2)
【分析】利用直角坐标系中的坐标的表示方法,可依次表示出四个地点的坐标。
四、作图题
12. 解:如图所示:△A1B1C1 , 即为所求,
A1(﹣3,﹣5);B1(﹣5,2);C1(3,﹣2).
【分析】利用方格纸的特点及轴对称的性质,分别作出点A、B、C关于x轴的对称点 A1、B1、C1 , 再首尾顺次相连即可得出所求的△ A1B1C1;结合图形即可写出点 A1、B1、C1的坐标。
13. 解:如图所示:
【分析】利用方格纸的特点及点的坐标与象限的关系即可分别描出各个点,再用线段按要求连接起来。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
