北师大版数学六年级下册1.2《圆柱的表面积》教案(表格版)
文档属性
| 名称 | 北师大版数学六年级下册1.2《圆柱的表面积》教案(表格版) |  | |
| 格式 | zip | ||
| 文件大小 | 20.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-31 07:52:11 | ||
图片预览



文档简介
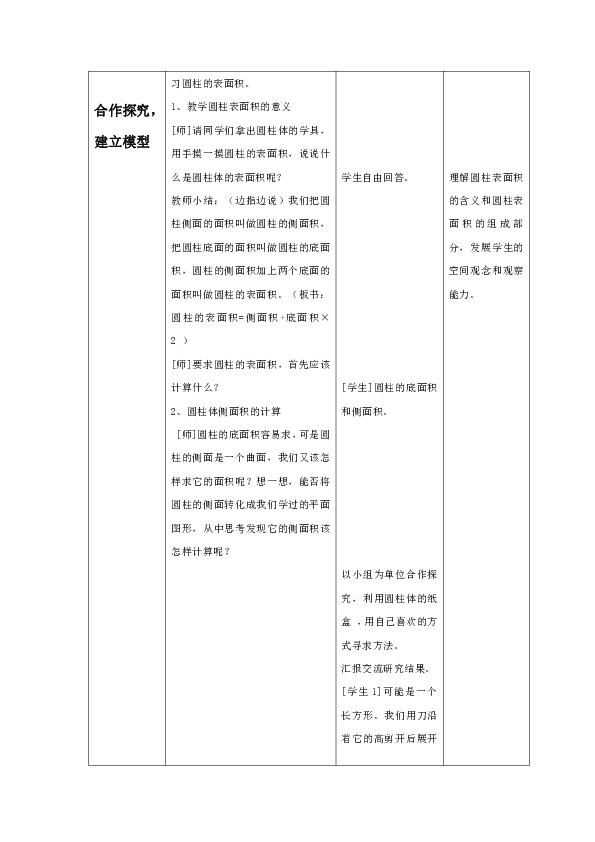
《圆柱的表面积》教学设计
课 题
北师大版六年级下册第一单元《圆柱的表面积》
课 型
新授课
课 时
第2课时
教学目标
知识目标
理解圆柱体侧面积和表面积的含义。
通过操作独立推导并掌握求圆柱的侧面积、表面积的方法,并能解决实际问题。
能力目标
培养学生观察、操作、概括的能力和利用所学知识合理灵活地分析、解决实际问题的能力。
情感目标
让学生进一步体会图形与实际生活的联系、感受立体图形学习价值。
教学重点
使学生掌握圆柱体表面积的计算方法,并能灵活运用圆柱表面积的计算方法解决生活中一些简单的问题。
教学难点
学生能够将展开图与圆柱体的各部分建立联系,并推导出圆柱侧面积、表面积的计算公式。
教具准备
教学PPT、圆柱体教具
学具准备
圆柱体的纸盒、剪刀、圆柱体学具
教学方法
谈话法、讨论法、练习法。
教学过程
教学步骤
教师活动
学生活动
设计意图
创设情境
导入新课
合作探究,建立模型
拓展应用,内化新知
回顾反思,总结概括
[师]俗话说只有量体裁剪做出来的衣服才合身,今天老师想让同学们一起做一个圆柱形纸盒。(课件出示圆柱体)想一想制作这个圆柱形纸盒如果接口不计,至少需要多大面积的纸板?实际上求的是圆柱的什么?
[师]今天这节课,我们就一起来学习圆柱的表面积。
1、教学圆柱表面积的意义
[师]请同学们拿出圆柱体的学具,用手摸一摸圆柱的表面积,说说什么是圆柱体的表面积呢?
教师小结:(边指边说)我们把圆柱侧面的面积叫做圆柱的侧面积,把圆柱底面的面积叫做圆柱的底面积,圆柱的侧面积加上两个底面的面积叫做圆柱的表面积。(板书:圆柱的表面积=侧面积+底面积×2 )
[师]要求圆柱的表面积,首先应该计算什么?
2、圆柱体侧面积的计算
[师]圆柱的底面积容易求,可是圆柱的侧面是一个曲面,我们又该怎样求它的面积呢?想一想,能否将圆柱的侧面转化成我们学过的平面图形,从中思考发现它的侧面积该怎样计算呢?
随着学生回答课件展示。
[师]圆柱体的侧面沿着高展开是一个长方形,你能说说这个长方形与圆柱有什么关系?
板书:
长方形的面积= 长 × 宽
圆柱的侧面积=底面周长× 高
S 侧 = C × h
[师]我们都知道圆柱体的侧面斜着剪下去,展开后是一个平行四边形,
你能说说平行四边形与圆柱体又有着怎样的关系呢?
计算圆柱表面积
[师]我们已经会求圆柱的侧面积,你现在会求圆柱的表面积了吗?
教师板书求表面积的算式。
[师]生活中,计算物体的表面积,经常要根据实际情况分析“需要计算哪些部分的面积”。
(课件出示习题)
做一个无盖的圆柱形铁皮水桶,底面直径为4分米,高为5分米,至少需要多大面积的铁皮?
启发学生说出:这道题是求做这个水桶要用铁皮多少平方厘米,实际上是求这个圆柱形水桶的表面积。题里告诉我们的“一个没有盖的圆柱形铁皮水桶”,计算时就是用侧面积加上一个底面积。
把一个圆柱形的薯片贺展开,是一个长18.84厘米,宽10厘米的长方形,这个薯片盒的侧面积是多少?表面积呢?
引导学生利用画图的方法找到长方形与圆柱的关系,明确长方形的面积等于圆柱的侧面积;要计算圆柱的表面积需找出圆柱的半径,已知长是18.84厘米,即底面周长是18.84厘米,根据r=C÷2π求得,继而求出圆柱的表面积。
谈谈本节课的收获。
[学生]圆柱的表面积。
学生自由回答。
[学生]圆柱的底面积和侧面积。
以小组为单位合作探究,利用圆柱体的纸盒 ,用自己喜欢的方式寻求方法。
汇报交流研究结果。
[学生1]可能是一个长方形。我们用刀沿着它的高剪开后展开发现正好是一个长方形。
[学生2]平时我们可以用一张长方形的纸卷成一个圆柱,所以侧面展开一定是一个长方形。
[学生3]不一定要沿着圆柱的高剪开。斜着剪开后展开是一个平行四边形。
[学生]长方形的长是圆柱体底面周长、长方形的宽是圆柱体的高。
学生动手操作,动笔验证,得出了同样的结论。
学生回答,并口头列式。
侧面积:3.14×2×10×30=1884(平方厘米)
底面积:3.14×102=314(平方厘米)
表面积:1884+314×2=2512(平方厘米)
答:做圆柱形纸盒需用2512平方厘米的纸板。
学生独立计算,并汇报答案,集体订正。
水桶的侧面积:3.14×4×5=62.8(平方分米)
水桶的底面积:3.14×(4÷2)2=12.56(平方分米)
需要铁皮:62.8+12.56=75.36(平方分米)
答:做这个水桶要用75.36平方分米的铁皮。
学生独立计算,并汇报答案,集体订正。
圆柱的侧面积:18.84×10=188.4(平方厘米)
底面积:3.14×(18.84÷3.14÷2)2=28.26(平方厘米)
表面积:188.4+28.26×2=244.92(平方厘米)
答:这个薯片盒的侧面积是188.4平方厘米,表面积是244.92平方厘米。
学生自由谈一谈。
创设“制作圆
柱形纸盒”,激发学生的求知欲,也体现出学数学的价值。
理解圆柱表面积的含义和圆柱表面积的组成部分,发展学生的空间观念和观察能力。
用小组合作的方式进行探究性学习,把曲面转化为已经学习过的平面图形,通过一系列的动手操作活动,发展学生分析问题、解决问题的能力,提高学生的动手操作、合作学习的能力、总纳概括的能力。
计算情境中圆柱形纸盒子的面积,以应用所学知识,使学生体会成功的快乐,获得良好的情感体验。
联系实际,灵活地运用圆柱表面积的计算方法解决实际问题,使学生体会到在生活中,有时要计算全部面面积的总和,有时是计算一个底面面积加上侧面积,还有时只是计算圆柱的侧面积,要根据实际灵活地选择有关数据进行计算。
此练习题的设计主要是让学生掌握侧面展开的长方形与圆柱的关系,明确长方形的面积等于圆柱的侧面积,长方形的长等于圆柱的底面周长,灵活运用圆的周长公式计算圆柱的半径。
通过总结梳理知识,培养学生归纳总结的习惯。
板书设计
圆柱的表面积
圆柱的表面积==侧面积+底面积×2
长方形的面积= 长 × 宽
圆柱的侧面积=底面周长× 高
S 侧 = C × h
侧面积:3.14×2×10×30=1884(平方厘米)
底面积:3.14×102=314(平方厘米)
表面积:1884+314×2=2512(平方厘米)
答:做圆柱形纸盒需用2512平方厘米的纸板。
课 题
北师大版六年级下册第一单元《圆柱的表面积》
课 型
新授课
课 时
第2课时
教学目标
知识目标
理解圆柱体侧面积和表面积的含义。
通过操作独立推导并掌握求圆柱的侧面积、表面积的方法,并能解决实际问题。
能力目标
培养学生观察、操作、概括的能力和利用所学知识合理灵活地分析、解决实际问题的能力。
情感目标
让学生进一步体会图形与实际生活的联系、感受立体图形学习价值。
教学重点
使学生掌握圆柱体表面积的计算方法,并能灵活运用圆柱表面积的计算方法解决生活中一些简单的问题。
教学难点
学生能够将展开图与圆柱体的各部分建立联系,并推导出圆柱侧面积、表面积的计算公式。
教具准备
教学PPT、圆柱体教具
学具准备
圆柱体的纸盒、剪刀、圆柱体学具
教学方法
谈话法、讨论法、练习法。
教学过程
教学步骤
教师活动
学生活动
设计意图
创设情境
导入新课
合作探究,建立模型
拓展应用,内化新知
回顾反思,总结概括
[师]俗话说只有量体裁剪做出来的衣服才合身,今天老师想让同学们一起做一个圆柱形纸盒。(课件出示圆柱体)想一想制作这个圆柱形纸盒如果接口不计,至少需要多大面积的纸板?实际上求的是圆柱的什么?
[师]今天这节课,我们就一起来学习圆柱的表面积。
1、教学圆柱表面积的意义
[师]请同学们拿出圆柱体的学具,用手摸一摸圆柱的表面积,说说什么是圆柱体的表面积呢?
教师小结:(边指边说)我们把圆柱侧面的面积叫做圆柱的侧面积,把圆柱底面的面积叫做圆柱的底面积,圆柱的侧面积加上两个底面的面积叫做圆柱的表面积。(板书:圆柱的表面积=侧面积+底面积×2 )
[师]要求圆柱的表面积,首先应该计算什么?
2、圆柱体侧面积的计算
[师]圆柱的底面积容易求,可是圆柱的侧面是一个曲面,我们又该怎样求它的面积呢?想一想,能否将圆柱的侧面转化成我们学过的平面图形,从中思考发现它的侧面积该怎样计算呢?
随着学生回答课件展示。
[师]圆柱体的侧面沿着高展开是一个长方形,你能说说这个长方形与圆柱有什么关系?
板书:
长方形的面积= 长 × 宽
圆柱的侧面积=底面周长× 高
S 侧 = C × h
[师]我们都知道圆柱体的侧面斜着剪下去,展开后是一个平行四边形,
你能说说平行四边形与圆柱体又有着怎样的关系呢?
计算圆柱表面积
[师]我们已经会求圆柱的侧面积,你现在会求圆柱的表面积了吗?
教师板书求表面积的算式。
[师]生活中,计算物体的表面积,经常要根据实际情况分析“需要计算哪些部分的面积”。
(课件出示习题)
做一个无盖的圆柱形铁皮水桶,底面直径为4分米,高为5分米,至少需要多大面积的铁皮?
启发学生说出:这道题是求做这个水桶要用铁皮多少平方厘米,实际上是求这个圆柱形水桶的表面积。题里告诉我们的“一个没有盖的圆柱形铁皮水桶”,计算时就是用侧面积加上一个底面积。
把一个圆柱形的薯片贺展开,是一个长18.84厘米,宽10厘米的长方形,这个薯片盒的侧面积是多少?表面积呢?
引导学生利用画图的方法找到长方形与圆柱的关系,明确长方形的面积等于圆柱的侧面积;要计算圆柱的表面积需找出圆柱的半径,已知长是18.84厘米,即底面周长是18.84厘米,根据r=C÷2π求得,继而求出圆柱的表面积。
谈谈本节课的收获。
[学生]圆柱的表面积。
学生自由回答。
[学生]圆柱的底面积和侧面积。
以小组为单位合作探究,利用圆柱体的纸盒 ,用自己喜欢的方式寻求方法。
汇报交流研究结果。
[学生1]可能是一个长方形。我们用刀沿着它的高剪开后展开发现正好是一个长方形。
[学生2]平时我们可以用一张长方形的纸卷成一个圆柱,所以侧面展开一定是一个长方形。
[学生3]不一定要沿着圆柱的高剪开。斜着剪开后展开是一个平行四边形。
[学生]长方形的长是圆柱体底面周长、长方形的宽是圆柱体的高。
学生动手操作,动笔验证,得出了同样的结论。
学生回答,并口头列式。
侧面积:3.14×2×10×30=1884(平方厘米)
底面积:3.14×102=314(平方厘米)
表面积:1884+314×2=2512(平方厘米)
答:做圆柱形纸盒需用2512平方厘米的纸板。
学生独立计算,并汇报答案,集体订正。
水桶的侧面积:3.14×4×5=62.8(平方分米)
水桶的底面积:3.14×(4÷2)2=12.56(平方分米)
需要铁皮:62.8+12.56=75.36(平方分米)
答:做这个水桶要用75.36平方分米的铁皮。
学生独立计算,并汇报答案,集体订正。
圆柱的侧面积:18.84×10=188.4(平方厘米)
底面积:3.14×(18.84÷3.14÷2)2=28.26(平方厘米)
表面积:188.4+28.26×2=244.92(平方厘米)
答:这个薯片盒的侧面积是188.4平方厘米,表面积是244.92平方厘米。
学生自由谈一谈。
创设“制作圆
柱形纸盒”,激发学生的求知欲,也体现出学数学的价值。
理解圆柱表面积的含义和圆柱表面积的组成部分,发展学生的空间观念和观察能力。
用小组合作的方式进行探究性学习,把曲面转化为已经学习过的平面图形,通过一系列的动手操作活动,发展学生分析问题、解决问题的能力,提高学生的动手操作、合作学习的能力、总纳概括的能力。
计算情境中圆柱形纸盒子的面积,以应用所学知识,使学生体会成功的快乐,获得良好的情感体验。
联系实际,灵活地运用圆柱表面积的计算方法解决实际问题,使学生体会到在生活中,有时要计算全部面面积的总和,有时是计算一个底面面积加上侧面积,还有时只是计算圆柱的侧面积,要根据实际灵活地选择有关数据进行计算。
此练习题的设计主要是让学生掌握侧面展开的长方形与圆柱的关系,明确长方形的面积等于圆柱的侧面积,长方形的长等于圆柱的底面周长,灵活运用圆的周长公式计算圆柱的半径。
通过总结梳理知识,培养学生归纳总结的习惯。
板书设计
圆柱的表面积
圆柱的表面积==侧面积+底面积×2
长方形的面积= 长 × 宽
圆柱的侧面积=底面周长× 高
S 侧 = C × h
侧面积:3.14×2×10×30=1884(平方厘米)
底面积:3.14×102=314(平方厘米)
表面积:1884+314×2=2512(平方厘米)
答:做圆柱形纸盒需用2512平方厘米的纸板。
