五年级下册数学总复习课件-复习长方体和正方体-人教新课(共36张PPT)
文档属性
| 名称 | 五年级下册数学总复习课件-复习长方体和正方体-人教新课(共36张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-31 07:38:03 | ||
图片预览






文档简介
(共36张PPT)
复习长方体和正方体
长方形
正方形
三角形
按边分
按角分
等边三角形
等腰三角形
一般三角形
锐角三角形
直角角三角形
钝角三角形
平行四边形
梯形
等腰梯形
直角梯形
一般梯形
组合图形
平面图形
一、建构知识网络
立体图形
正方体
长方体
……
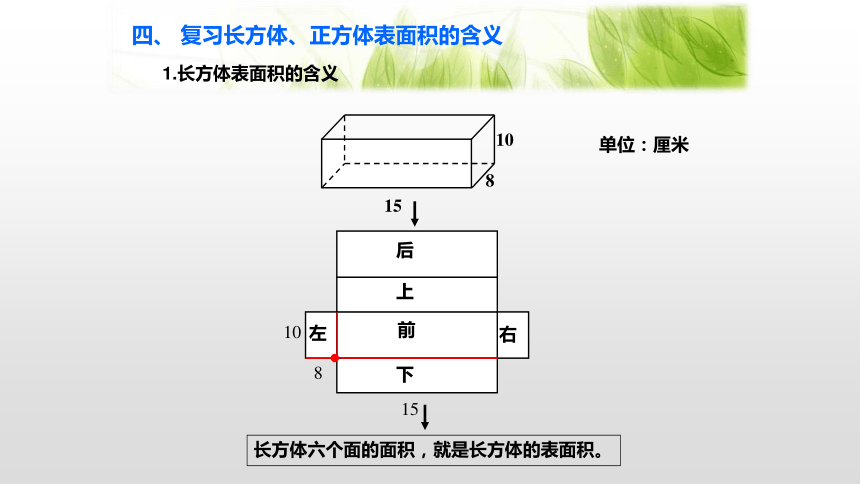
二、 注重知识的承接,回顾所学平面图形的特征、周长和面积公式。
名称 特征 周长(c) 面积(s)
长方形 两组对边分别平行且相等 (长+宽)×2
C=2(a+b) 长×宽
S=ab
正方形 四边相等 边长×4
C=4a 边长×边长
S=a?
平行四边形 两组对边平行且相等 底×高
S=ah
梯形 只有一组对边平行 (上底+下底)×高÷2
三角形 三条边,三个内角的和等于180° (底×高)÷2
ah
S=
1
2
(a+b)h
S=
1
2
三、 明确长方体、正方体的异同。
从点、棱、面三方面比较长方体和正方体之间的相同点和不同点
长方体 正方体
相同点 6个面、12条棱、8个顶点
不同点 6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。 6个面都是正方形,
6个面完全相同
相对棱的长度相等 12条棱长度都相等
正方体是特殊的长方体。
用集合图表示:
长方体
正方体
四、 复习长方体、正方体表面积的含义
15
10
8
后
前
上
下
左
右
●
15
10
8
单位:厘米
长方体六个面的面积,就是长方体的表面积。
1.长方体表面积的含义
2.正方体表面积的含义
(1)正方体棱长与每个面边长的关系
后
上
前
下
左
右
正方体展开图的每个面都是正方形,边长就是正方体的棱长,每个面的面积都等于棱长乘棱长。
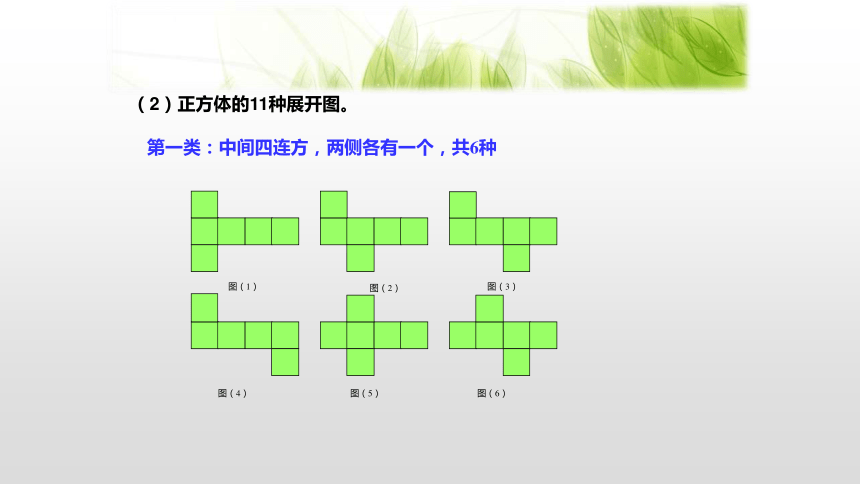
(2)正方体的11种展开图。
图(1)
图(2)
图(3)
图(4)
图(5)
图(6)
第一类:中间四连方,两侧各有一个,共6种
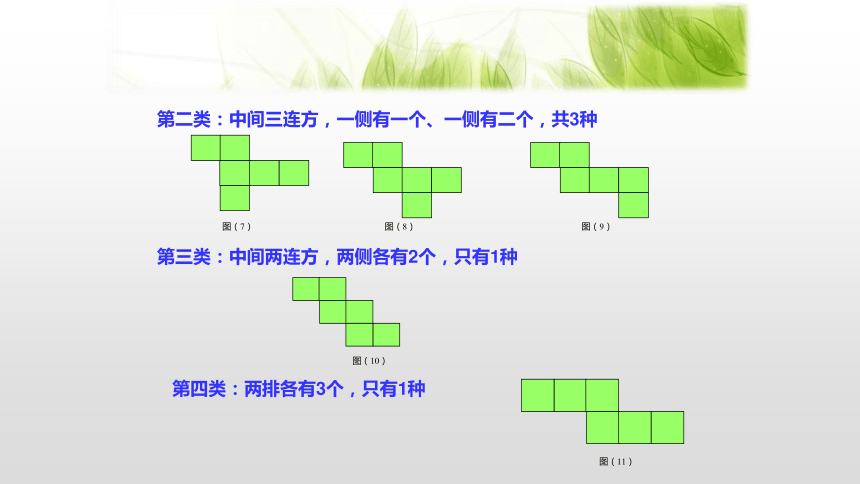
第二类:中间三连方,一侧有一个、一侧有二个,共3种
图(7)
图(8)
图(9)
第三类:中间两连方,两侧各有2个,只有1种
图(10)
第四类:两排各有3个,只有1种
图(11)
五、复习长方体、正方体体积公式的推导
(书本P29页)
长方体的体积 = 长 × 宽 × 高
底面积
正方体的体积 = 棱长 ×棱长×棱长
底面积
可看作是高
长方体(或正方体)的
体积 = 底面积 × 高
六、体积与容积区别与联系
异同点 体积 容积
区别 意义不同 物体所占空间的大小,叫做物体的体积。 一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同 从物体外部测量长、宽、高。 从容器里面测量长、宽、高。
单位名称不同 m?、dm?、cm?。 容积单位:L和ml;计量固体时用体积单位。
联系 容积的大小是通过所能容纳物体的体积表示出来的。
计算方法相同
7厘米
5厘米
5厘米
这个长方体的长是( )厘米,宽是( )厘米,高是( )厘米,这个长方体有( )个面是正方形,有( )个面是长方形。
如图
1.
2. 要焊接一个长10cm,宽8cm,高6cm的长方体框架,要准备10cm,宽8cm,高6cm的铁丝各( )根。共长( )cm
3.一个正方体纸盒的棱长是7cm,这个纸盒的棱长总和是(84 )cm。
4.有一根150cm长的铁丝,用这根铁丝焊成了一个正方体的框架,还剩铁丝6cm。这个正方体框架的棱长是( )厘米。
七、基础知识的练习
7
5
5
2
4
4
96
(长+宽+高)×4
棱长×12
12
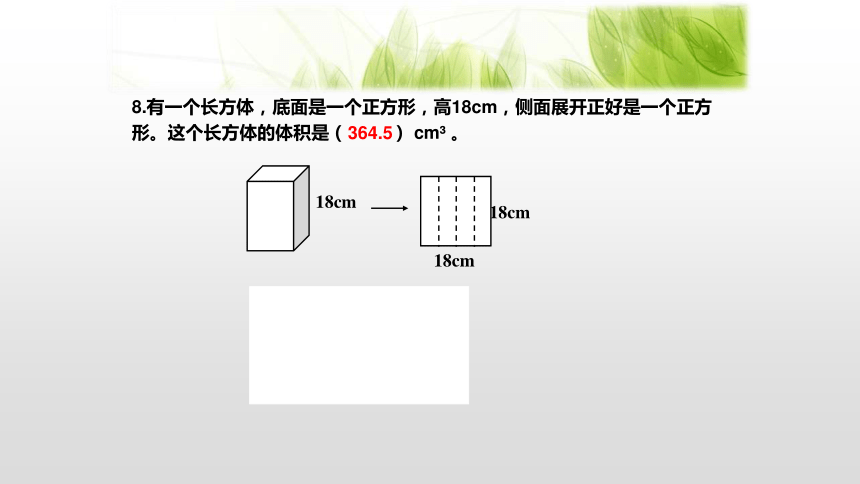
8.有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是( ) cm? 。
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
18cm
18cm
18cm
364.5
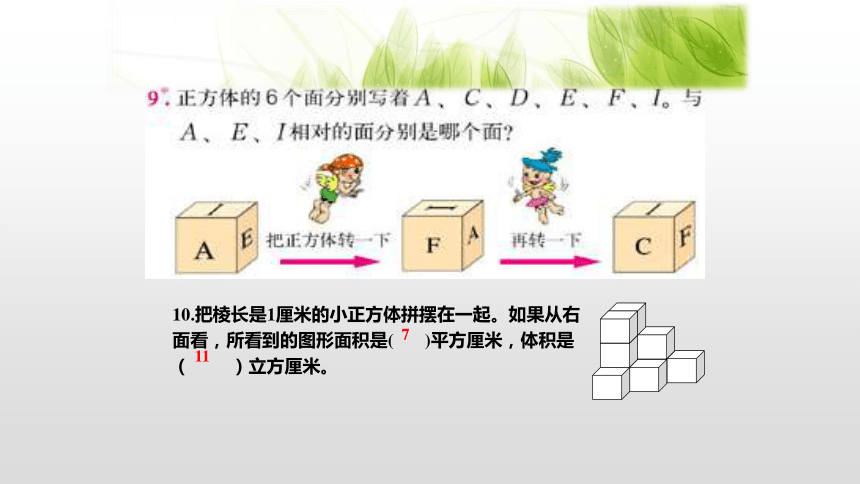
10.把棱长是1厘米的小正方体拼摆在一起。如果从右面看,所看到的图形面积是( )平方厘米,体积是( )立方厘米。
7
11
11.
一个棱长为2cm的正方体,在它的一个角上挖掉一个棱长为1cm的小正方体,它的表面积是 (?? ? )cm?。
24
第二课时:解决相关的实际问题
12cm
15cm
8cm
1. 一条彩带捆扎一种礼盒(如图),如果接头处的彩带长30cm,求这条彩带的长度。
8×4+12×2+15×2+30=116(cm)
答:这条彩带长116厘米。
2.与右面正方体一致的展开图是( )。
B
1
2
3
1
2
3
2
3
1
1
2
3
C
B
A
甲
乙
取出石块后
2.1dm
1.8dm
3. 图中有两个完全一样的长方体水箱,水箱的底面积是2平方分米,请结合图中所给信息求出甲箱中石块的体积是多少?
2×(2.1-1.8)=0.6(dm?)
答:石块的体积是0.6dm?。
前
右
6
3
7
4.小明从一个长方体纸盒上撕下两个相邻的面(展开后如图,单位:厘米),这个纸盒的底面积是( )平方厘米,体积是( )立方厘米。
底面积:6×3=18(平方厘米)
18
126
体积:6×3×7=126(立方厘米)
5厘米
5厘米
5厘米
5.把 积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
(25÷5)×(20÷5)×(20÷5)
=5×4×4
=80(块)
答:纸箱最多可容纳积木80块。
6.把 积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
5厘米
3厘米
3厘米
(25÷3)×(20÷3)×(20÷5)
≈8×6×4
=192(块)
答:纸箱最多可容纳积木192块。
7.一块长方形铁皮,长40cm,宽30cm,像下图这样从4个角各剪掉一个边长为5厘米的正方形,然后做成盒子,这个盒子的容积是多少升?
40cm
30cm
(40-5×2)×(30-5×2)×5=3000(cm?)
3000cm?=3L
答:这个盒子的容积是3升。
12ml=12cm3 24ml=24cm3
一个小球的体积:(24-12) ÷(4-1)=4(cm3)
一个大球的体积:12-4=8(cm3)
左图长、宽、高分别是4cm、3cm、3cm。
它的体积是:
4×3×3=36(cm2)
右图长、宽、高分别是4cm、3cm、4cm。
它的体积是:
4×3×4=48(cm2)
10.用3个长5cm,宽4cm,高3cm的长方体木块,拼成一个表面积最小的长方体。这个长方体的表面积是多少平方厘米?
5cm
4cm
3cm
[5×4+5×(3×3)+4×(3×3)]×2=(20+45+36)×2=202(cm?)
答:这个长方体的表面积是202平方厘米。
3cm
2cm
6cm
6cm
11.有一个形状如图的零件,由一个长方体和一个
正方体组合而成。长方体的长和宽都是6cm,高是3cm,正方体的棱长是2cm。求这个零件的表面积。
2×2×4+6×3×4+6×6×2
=16+72+72
=160(cm?)
答:这个零件的表面积是160平方厘米。
12.由27个棱长为1cm的小正方体组成一个棱长为3cm的大正方体,若自上而下去掉中间的3个小正方体(如图所示),则剩下的几何体的表面积是多少平方厘米?
3×3×6-1×1×2+3×1×4
=54-2+12
=64(cm?)
答:剩下的几何体的表面积是64平方厘米。
13.从一个大长方体上切下一个体积是128立方厘米的小长方体(如图)。原来大长方体的体积是多少立方厘米?
22cm
8cm
切下部分
128÷8×22
=16×22
=352(立方厘米)
答:原来大长方体的体积是352立方厘米。
14. 一个密封的长方体容器里面装有一些水,水深9厘米,如果把这个容器的右面做底,这时容器内的水深多少厘米?
36
10
12
36
10
12
36×10×9=3240(cm3)
3240÷(12×10)=27(cm)
答:容器内的水深27厘米。
二、注重知识的把握
意义 性质 特征
轴对称 把一个图形沿着一条直线折叠,如果它能够与另一个图形重合,那么这两个图形成轴对称。这条直线就是对称轴。 对称点到对称轴的距离相等。 沿对称轴对折,对称点、对称线段、对称角度重合。
旋转 物体绕着某一点或轴运动,这种运动现象称为旋转。 图形绕着某一点旋转一定的度数,图形的对称点、对称线段都旋转相应的度数,对应点到旋转点的距离相等,对应的线段、对应的角都相等。 图形旋转后,形状、大小都没有发生变化,只是位置变化了。
平移 对应点所连接的线段平行且相等。
旋转三要素:旋转点(或旋转中心)、旋转方向、旋转角度
注意意义的区别
轴对称是沿着一条直线对折后,两个图形能够完全重合;
轴对称图形是指一个图形沿着一条直线对折后,图形的两部分之间能够完全重合。
轴对称图形是指一个图形,而大小形状完全相同的两个图形才能成轴对称。
(二)简单图形旋转90°的画法
1.找出图形的关键点或线段。
2.借助三角板(或量角器)作原图形线段或关键点与旋转中心所在线段的垂线。
3.在所做垂线上量出与原线段相等的长度(即找出原图关键点的对应点)。
4.顺次连接所画出的对应点。
(1)画出图①的全部对称轴。
(2)画出图②向上平移3格后的图形。
图① 图②
A
O
B
(3)画出绕点O ,顺时针旋转90 后的图形。
A
O
B
A'
A
O
B
A'
A
O
B
A'
B'
A
O
B
A'
B'
四、注重空间观念的训练
(图一)三角形绕点O( )时针旋转了( )度。
(图二)三角形绕点 O ( )时针旋转了( )度。
逆
90
顺
90
旋转不改变图形的形状 、大小 ,只改变图形的 位置 。
图(二)
o
图(一)
o
复习长方体和正方体
长方形
正方形
三角形
按边分
按角分
等边三角形
等腰三角形
一般三角形
锐角三角形
直角角三角形
钝角三角形
平行四边形
梯形
等腰梯形
直角梯形
一般梯形
组合图形
平面图形
一、建构知识网络
立体图形
正方体
长方体
……
二、 注重知识的承接,回顾所学平面图形的特征、周长和面积公式。
名称 特征 周长(c) 面积(s)
长方形 两组对边分别平行且相等 (长+宽)×2
C=2(a+b) 长×宽
S=ab
正方形 四边相等 边长×4
C=4a 边长×边长
S=a?
平行四边形 两组对边平行且相等 底×高
S=ah
梯形 只有一组对边平行 (上底+下底)×高÷2
三角形 三条边,三个内角的和等于180° (底×高)÷2
ah
S=
1
2
(a+b)h
S=
1
2
三、 明确长方体、正方体的异同。
从点、棱、面三方面比较长方体和正方体之间的相同点和不同点
长方体 正方体
相同点 6个面、12条棱、8个顶点
不同点 6个面都是长方形(有时相对的两个面是正方形),相对面完全相同。 6个面都是正方形,
6个面完全相同
相对棱的长度相等 12条棱长度都相等
正方体是特殊的长方体。
用集合图表示:
长方体
正方体
四、 复习长方体、正方体表面积的含义
15
10
8
后
前
上
下
左
右
●
15
10
8
单位:厘米
长方体六个面的面积,就是长方体的表面积。
1.长方体表面积的含义
2.正方体表面积的含义
(1)正方体棱长与每个面边长的关系
后
上
前
下
左
右
正方体展开图的每个面都是正方形,边长就是正方体的棱长,每个面的面积都等于棱长乘棱长。
(2)正方体的11种展开图。
图(1)
图(2)
图(3)
图(4)
图(5)
图(6)
第一类:中间四连方,两侧各有一个,共6种
第二类:中间三连方,一侧有一个、一侧有二个,共3种
图(7)
图(8)
图(9)
第三类:中间两连方,两侧各有2个,只有1种
图(10)
第四类:两排各有3个,只有1种
图(11)
五、复习长方体、正方体体积公式的推导
(书本P29页)
长方体的体积 = 长 × 宽 × 高
底面积
正方体的体积 = 棱长 ×棱长×棱长
底面积
可看作是高
长方体(或正方体)的
体积 = 底面积 × 高
六、体积与容积区别与联系
异同点 体积 容积
区别 意义不同 物体所占空间的大小,叫做物体的体积。 一个容器所能容纳物体的体积,叫做这个容器的容积。
测量方法不同 从物体外部测量长、宽、高。 从容器里面测量长、宽、高。
单位名称不同 m?、dm?、cm?。 容积单位:L和ml;计量固体时用体积单位。
联系 容积的大小是通过所能容纳物体的体积表示出来的。
计算方法相同
7厘米
5厘米
5厘米
这个长方体的长是( )厘米,宽是( )厘米,高是( )厘米,这个长方体有( )个面是正方形,有( )个面是长方形。
如图
1.
2. 要焊接一个长10cm,宽8cm,高6cm的长方体框架,要准备10cm,宽8cm,高6cm的铁丝各( )根。共长( )cm
3.一个正方体纸盒的棱长是7cm,这个纸盒的棱长总和是(84 )cm。
4.有一根150cm长的铁丝,用这根铁丝焊成了一个正方体的框架,还剩铁丝6cm。这个正方体框架的棱长是( )厘米。
七、基础知识的练习
7
5
5
2
4
4
96
(长+宽+高)×4
棱长×12
12
8.有一个长方体,底面是一个正方形,高18cm,侧面展开正好是一个正方形。这个长方体的体积是( ) cm? 。
18÷4=4.5(cm)
4.5×4.5×18
=20.25×18
=364.5(cm?)
18cm
18cm
18cm
364.5
10.把棱长是1厘米的小正方体拼摆在一起。如果从右面看,所看到的图形面积是( )平方厘米,体积是( )立方厘米。
7
11
11.
一个棱长为2cm的正方体,在它的一个角上挖掉一个棱长为1cm的小正方体,它的表面积是 (?? ? )cm?。
24
第二课时:解决相关的实际问题
12cm
15cm
8cm
1. 一条彩带捆扎一种礼盒(如图),如果接头处的彩带长30cm,求这条彩带的长度。
8×4+12×2+15×2+30=116(cm)
答:这条彩带长116厘米。
2.与右面正方体一致的展开图是( )。
B
1
2
3
1
2
3
2
3
1
1
2
3
C
B
A
甲
乙
取出石块后
2.1dm
1.8dm
3. 图中有两个完全一样的长方体水箱,水箱的底面积是2平方分米,请结合图中所给信息求出甲箱中石块的体积是多少?
2×(2.1-1.8)=0.6(dm?)
答:石块的体积是0.6dm?。
前
右
6
3
7
4.小明从一个长方体纸盒上撕下两个相邻的面(展开后如图,单位:厘米),这个纸盒的底面积是( )平方厘米,体积是( )立方厘米。
底面积:6×3=18(平方厘米)
18
126
体积:6×3×7=126(立方厘米)
5厘米
5厘米
5厘米
5.把 积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
(25÷5)×(20÷5)×(20÷5)
=5×4×4
=80(块)
答:纸箱最多可容纳积木80块。
6.把 积木装入纸箱内,纸箱从里面量,长25厘米,宽和高都是20厘米。纸箱最多可容纳积木多少块?
5厘米
3厘米
3厘米
(25÷3)×(20÷3)×(20÷5)
≈8×6×4
=192(块)
答:纸箱最多可容纳积木192块。
7.一块长方形铁皮,长40cm,宽30cm,像下图这样从4个角各剪掉一个边长为5厘米的正方形,然后做成盒子,这个盒子的容积是多少升?
40cm
30cm
(40-5×2)×(30-5×2)×5=3000(cm?)
3000cm?=3L
答:这个盒子的容积是3升。
12ml=12cm3 24ml=24cm3
一个小球的体积:(24-12) ÷(4-1)=4(cm3)
一个大球的体积:12-4=8(cm3)
左图长、宽、高分别是4cm、3cm、3cm。
它的体积是:
4×3×3=36(cm2)
右图长、宽、高分别是4cm、3cm、4cm。
它的体积是:
4×3×4=48(cm2)
10.用3个长5cm,宽4cm,高3cm的长方体木块,拼成一个表面积最小的长方体。这个长方体的表面积是多少平方厘米?
5cm
4cm
3cm
[5×4+5×(3×3)+4×(3×3)]×2=(20+45+36)×2=202(cm?)
答:这个长方体的表面积是202平方厘米。
3cm
2cm
6cm
6cm
11.有一个形状如图的零件,由一个长方体和一个
正方体组合而成。长方体的长和宽都是6cm,高是3cm,正方体的棱长是2cm。求这个零件的表面积。
2×2×4+6×3×4+6×6×2
=16+72+72
=160(cm?)
答:这个零件的表面积是160平方厘米。
12.由27个棱长为1cm的小正方体组成一个棱长为3cm的大正方体,若自上而下去掉中间的3个小正方体(如图所示),则剩下的几何体的表面积是多少平方厘米?
3×3×6-1×1×2+3×1×4
=54-2+12
=64(cm?)
答:剩下的几何体的表面积是64平方厘米。
13.从一个大长方体上切下一个体积是128立方厘米的小长方体(如图)。原来大长方体的体积是多少立方厘米?
22cm
8cm
切下部分
128÷8×22
=16×22
=352(立方厘米)
答:原来大长方体的体积是352立方厘米。
14. 一个密封的长方体容器里面装有一些水,水深9厘米,如果把这个容器的右面做底,这时容器内的水深多少厘米?
36
10
12
36
10
12
36×10×9=3240(cm3)
3240÷(12×10)=27(cm)
答:容器内的水深27厘米。
二、注重知识的把握
意义 性质 特征
轴对称 把一个图形沿着一条直线折叠,如果它能够与另一个图形重合,那么这两个图形成轴对称。这条直线就是对称轴。 对称点到对称轴的距离相等。 沿对称轴对折,对称点、对称线段、对称角度重合。
旋转 物体绕着某一点或轴运动,这种运动现象称为旋转。 图形绕着某一点旋转一定的度数,图形的对称点、对称线段都旋转相应的度数,对应点到旋转点的距离相等,对应的线段、对应的角都相等。 图形旋转后,形状、大小都没有发生变化,只是位置变化了。
平移 对应点所连接的线段平行且相等。
旋转三要素:旋转点(或旋转中心)、旋转方向、旋转角度
注意意义的区别
轴对称是沿着一条直线对折后,两个图形能够完全重合;
轴对称图形是指一个图形沿着一条直线对折后,图形的两部分之间能够完全重合。
轴对称图形是指一个图形,而大小形状完全相同的两个图形才能成轴对称。
(二)简单图形旋转90°的画法
1.找出图形的关键点或线段。
2.借助三角板(或量角器)作原图形线段或关键点与旋转中心所在线段的垂线。
3.在所做垂线上量出与原线段相等的长度(即找出原图关键点的对应点)。
4.顺次连接所画出的对应点。
(1)画出图①的全部对称轴。
(2)画出图②向上平移3格后的图形。
图① 图②
A
O
B
(3)画出绕点O ,顺时针旋转90 后的图形。
A
O
B
A'
A
O
B
A'
A
O
B
A'
B'
A
O
B
A'
B'
四、注重空间观念的训练
(图一)三角形绕点O( )时针旋转了( )度。
(图二)三角形绕点 O ( )时针旋转了( )度。
逆
90
顺
90
旋转不改变图形的形状 、大小 ,只改变图形的 位置 。
图(二)
o
图(一)
o
