3.3 解一元一次方程(二)——去括号与去分母 课件
文档属性
| 名称 | 3.3 解一元一次方程(二)——去括号与去分母 课件 |  | |
| 格式 | rar | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-31 14:58:48 | ||
图片预览






文档简介
(共17张PPT)
3.3 解一元一次方程
——去括号与去分母
数学人教版 七年级上
学习目标
1、理解去括号和去分母的依据和作用,掌握去括号与去分母解一
元一次方程的方法.
2、从实际问题中列出一元一次方程,会将实际问题转化为数学问
题.
3、经历列方程和解方程的过程,进一步体会方程模型思想与化归
思想的作用.
当方程的形式较复杂时,解方程的步骤也相应的更多些.本节
重点讨论如何利用“去括号”和“去分母”解一元一次方程.
新知导入
问题1:某工厂加强节能措施,去年下半年与上半年相比,用平均用电量减少2000kw/h(千瓦/时),全年用电15万w/h.这个工厂去年上半年每月平均用电是多少?
新知讲解
解:
设上半年每月平均用电 x kw·h.则下半年每月平均用电(
x-2000)kw·h;上半年共用电 6x kw·h,下半年共用电6(x-
2000)kw·h.
根据全年用电15万kw·h,列得方程
6x+6(x-2000)=150000.
如果去括号,就能简化方程的形式.
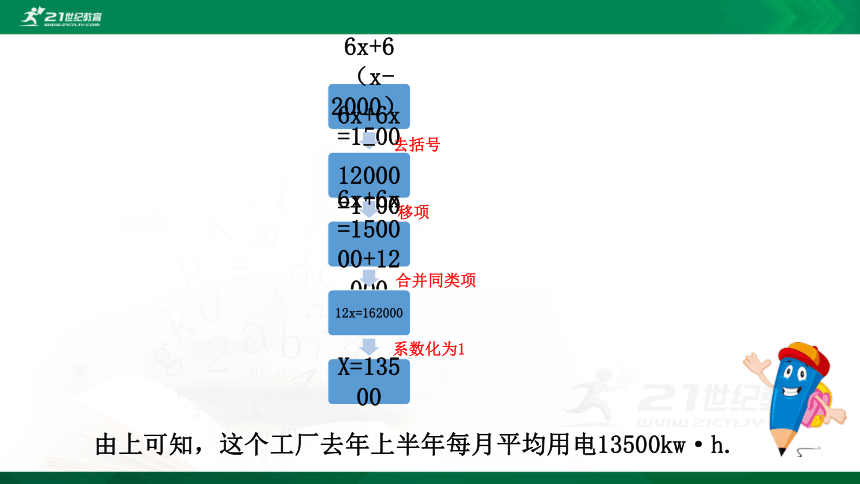
下面的框图表示了解这个方程的流程.
1kw·h的电量即1kw的电器1h的用电量.
去括号
移项
合并同类项
系数化为1
由上可知,这个工厂去年上半年每月平均用电13500kw·h.
问题2:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.
这个问题可以用现在的数学符号表示.设这个数是x.根据题意,得方程
这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,
则可使解方程中的计算更简便些.
我们知道,等式两边乘以同一个数,结果仍相等.这个方程中
各分母的最小公倍数是42,方程两边乘42,得
即
28x+21x+6x+42x=1386
合并同类项,得
97x=1386
系数化为1,得
注意:方程的每一项都要乘以42.
课堂例题
例1 解下列方程
(1)2x-(x+10)=5x+2(x-1);
(2)3x-7(x-1)=3-2(x+3).
解:(1)去括号,得
2x-x-10=5x+2x-2
移项,得
2x-x-5x-2x=-2+10
合并同类项,得
-6x=8
系数化为1,得
X=-4/3
解:(1)去括号,得
3x-7x+7=3-2x-6
移项,得
3x-7x+2x=3-6-7
合并同类项,得
-2x=-10
系数化为1,得
X=5
例2 一艘船从甲码头到乙码头顺流而行,用了2h;从乙码头返回
甲码头逆流而行,用了2.5h.已知水流的速度是3km/h.求静在水中
的平均速度.
解:设船在静水中的平均速度为 x km/h,则顺流速度为(x+3)
km/h,逆流速度为(x-3)km/h.
根据往返路程相等,列得
2(x+3)=2.5(x-3)
去括号,得
2x+6=2.5x-7.5
移项及合并同类项,得
0.5x=13.5
系数化为1,得
X=27
例3 解下列方程
解:(1)去分母(方程两边乘4),得
2(x+1)-4=8+(2-x)
去括号,得
2x+2-4=8+2-x
移项,得
2x+x=8+2-2+4
合并同类项,得
3x=12
系数化为1,得
X=4
解:(1)去分母(方程两边乘6),得
18x+3(x-1)=18-2(2x-1)
去括号,得
18x+3x-3=18-4x+2
移项,得
18x+3x+4x=18+2+3
合并同类项,得
25x=23
系数化为1,得
X=23/25
课堂总结
1、本节课学了哪些主要内容,你觉得自己掌握这些知识了吗?
2、在解决问题时应该注意些什么?
作业布置
习题3.3 第1、3题和第5、6题.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
3.3 解一元一次方程
——去括号与去分母
数学人教版 七年级上
学习目标
1、理解去括号和去分母的依据和作用,掌握去括号与去分母解一
元一次方程的方法.
2、从实际问题中列出一元一次方程,会将实际问题转化为数学问
题.
3、经历列方程和解方程的过程,进一步体会方程模型思想与化归
思想的作用.
当方程的形式较复杂时,解方程的步骤也相应的更多些.本节
重点讨论如何利用“去括号”和“去分母”解一元一次方程.
新知导入
问题1:某工厂加强节能措施,去年下半年与上半年相比,用平均用电量减少2000kw/h(千瓦/时),全年用电15万w/h.这个工厂去年上半年每月平均用电是多少?
新知讲解
解:
设上半年每月平均用电 x kw·h.则下半年每月平均用电(
x-2000)kw·h;上半年共用电 6x kw·h,下半年共用电6(x-
2000)kw·h.
根据全年用电15万kw·h,列得方程
6x+6(x-2000)=150000.
如果去括号,就能简化方程的形式.
下面的框图表示了解这个方程的流程.
1kw·h的电量即1kw的电器1h的用电量.
去括号
移项
合并同类项
系数化为1
由上可知,这个工厂去年上半年每月平均用电13500kw·h.
问题2:一个数,它的三分之二,它的一半,它的七分之一,它的全部,加起来总共是33.
这个问题可以用现在的数学符号表示.设这个数是x.根据题意,得方程
这样的方程中有些系数是分数,如果能化去分母,把系数化为整数,
则可使解方程中的计算更简便些.
我们知道,等式两边乘以同一个数,结果仍相等.这个方程中
各分母的最小公倍数是42,方程两边乘42,得
即
28x+21x+6x+42x=1386
合并同类项,得
97x=1386
系数化为1,得
注意:方程的每一项都要乘以42.
课堂例题
例1 解下列方程
(1)2x-(x+10)=5x+2(x-1);
(2)3x-7(x-1)=3-2(x+3).
解:(1)去括号,得
2x-x-10=5x+2x-2
移项,得
2x-x-5x-2x=-2+10
合并同类项,得
-6x=8
系数化为1,得
X=-4/3
解:(1)去括号,得
3x-7x+7=3-2x-6
移项,得
3x-7x+2x=3-6-7
合并同类项,得
-2x=-10
系数化为1,得
X=5
例2 一艘船从甲码头到乙码头顺流而行,用了2h;从乙码头返回
甲码头逆流而行,用了2.5h.已知水流的速度是3km/h.求静在水中
的平均速度.
解:设船在静水中的平均速度为 x km/h,则顺流速度为(x+3)
km/h,逆流速度为(x-3)km/h.
根据往返路程相等,列得
2(x+3)=2.5(x-3)
去括号,得
2x+6=2.5x-7.5
移项及合并同类项,得
0.5x=13.5
系数化为1,得
X=27
例3 解下列方程
解:(1)去分母(方程两边乘4),得
2(x+1)-4=8+(2-x)
去括号,得
2x+2-4=8+2-x
移项,得
2x+x=8+2-2+4
合并同类项,得
3x=12
系数化为1,得
X=4
解:(1)去分母(方程两边乘6),得
18x+3(x-1)=18-2(2x-1)
去括号,得
18x+3x-3=18-4x+2
移项,得
18x+3x+4x=18+2+3
合并同类项,得
25x=23
系数化为1,得
X=23/25
课堂总结
1、本节课学了哪些主要内容,你觉得自己掌握这些知识了吗?
2、在解决问题时应该注意些什么?
作业布置
习题3.3 第1、3题和第5、6题.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
