“四招”判断函数零点个数
图片预览



文档简介
专题一
“四招”判断函数零点个数
函数方程思想是一种重要的数学思想方法,函数问题可以利用方程求解,方程解的情况可借助于函数的图象和性质求解.高考命题常常以基本初等函数为载体,主要考查以下三个方面:(1)零点所在区间——零点存在性定理;(2)二次方程根的分布问题;(3)判断零点的个数问题;(4)根据零点的情况确定参数的值或范围;(5)根据零点的情况讨论函数的性质或证明不等式等.本专题围绕函数零点个数的判断问题,例题说法,高效训练.
【典型例题】
第一招
应用函数性质,判定函数零点个数
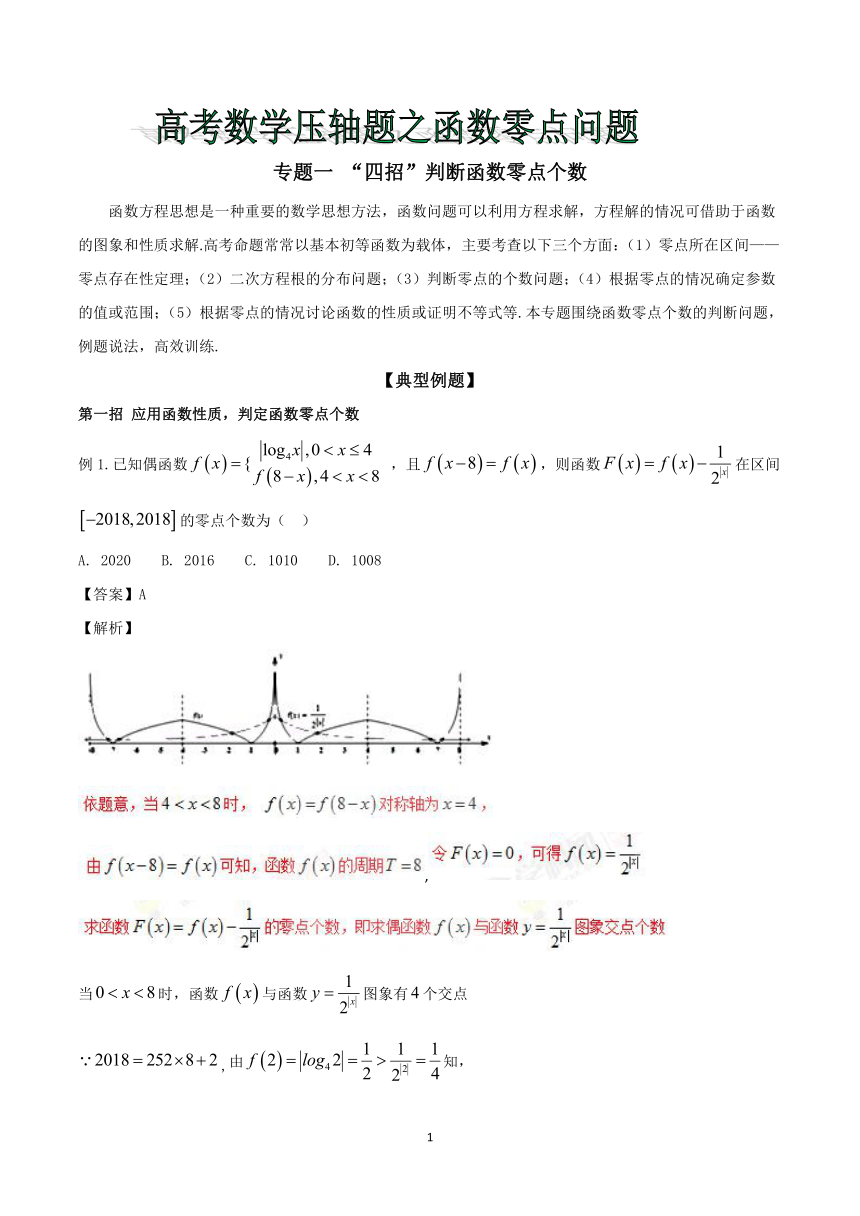
例1.已知偶函数,且,则函数在区间的零点个数为(
)
A.
2020
B.
2016
C.
1010
D.
1008
【答案】A
【解析】
,
当时,函数与函数图象有个交点
,由知,
当时函数与函数图象有个交点
故函数的零点个数为,故选.
第二招
数形结合,判定函数零点个数
例2.【2018届福建省永春一中、培元、季延、石光中学四校高三上第二次联考】定义在上的函数满足,且时,
;
时,
.
令,则函数的零点个数为(
)
A.
B.
C.
D.
【答案】B
,
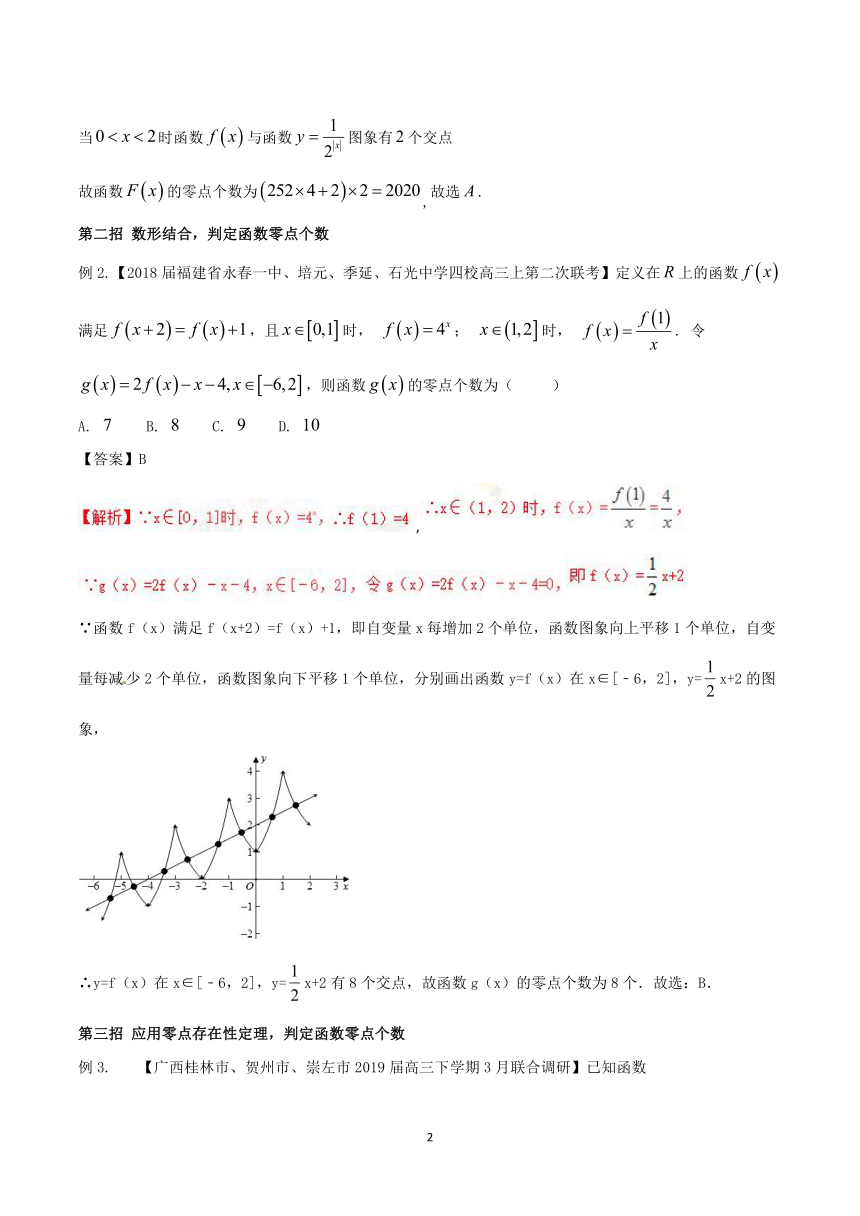
∵函数f(x)满足f(x+2)=f(x)+1,即自变量x每增加2个单位,函数图象向上平移1个单位,自变量每减少2个单位,函数图象向下平移1个单位,分别画出函数y=f(x)在x∈[﹣6,2],y=x+2的图象,
∴y=f(x)在x∈[﹣6,2],y=x+2有8个交点,故函数g(x)的零点个数为8个.故选:B.
第三招
应用零点存在性定理,判定函数零点个数
【广西桂林市、贺州市、崇左市2019届高三下学期3月联合调研】已知函数.(1)讨论的单调性;(2)讨论在上的零点个数.
∴当时,在上单调递增.
当时,在上单调递减,在上单调递增.
(2)设,则由(1)知
①当时,即,当时,,在单调递减
,
∴当,即,时,在上恒成立,
∴当时,在内无零点.
当,即,时,,
根据零点存在性定理知,此时,在内有零点,
∵在内单调递减,∴此时,在有一个零点.
②当时,即,当时,,在单调递增,
,.
∴当,即时,,根据零点存在性定理,此时,在内有零点.
∵在内单调递增,∴此时,在有一个零点.
当时,,∴此时,在无零点.
③当时,即,当时,;当时,;
则在单调递减,在单调递增.
∴在上恒成立,∴此时,在内无零点.
∴综上所述:当时,在内有1个零点;当时,在有一个零点;
当时,在无零点.
第四招
构造函数,判定函数零点个数
例4.【山东省菏泽市2019届高三上学期期末】已知函数f(x)=lnx+﹣1,a∈R.
(1)当a>0时,若函数f(x)在区间[1,3]上的最小值为,求a的值;
(2)讨论函数g(x)=f′(x)﹣零点的个数.
f’(x)min=f(a)=lna,令,得.
当a≥3时,f’(x)<0在(1,3)上恒成立,这时f(x)在[1,3]上为减函数,
∴,令得a=4﹣3ln3<2(舍去).
综上知.
(2)∵函数,
令g(x)=0,得.
设,,
当x∈(0,1)时,φ'(x)>0,此时φ(x)在(0,1)上单调递增,
当x∈(1,+∞)时,φ’(x)<0,此时φ(x)在(1,+∞)上单调递减,
所以x=1是φ(x)的唯一极值点,且是极大值点,因此x=1也是(x)的最大值点,
φ(x)的最大值为.
又φ(0)=0,结合φ(x)的图象可知:
①当时,函数g(x)无零点;
②当时,函数g(x)有且仅有一个零点;
③当时,函数g(x)有两个零点;
④a≤0时,函数g(x)有且只有一个零点;
综上所述,当时,函数g(x)无零点;当或a≤0时,函数g(x)有且仅有一个零点;
当时,函数g(x)有两个零点.
【规律与方法】
函数零点个数的求解与判断:
(1)直接求零点:令,如果能求出解,则有几个解就有几个零点;
(2)零点存在性定理:利用定理不仅要函数在区间上是连续不断的曲线,且,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点;
(3)利用图象交点的个数:将函数变形为两个函数的差,画两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.
(4)构造函数模型,判断零点个数.构造函数可根据题目不同,直接做差构造函数、分离参数后构造函数、先求导数再构造函数、先换元再构造函数等.
【提升训练】
1.【浙江省杭州地区(含周边)重点中学2019届高三上期中】已知定义在R上的奇函数,满足当时,则关于x的方程满足
A.对任意,恰有一解
B.对任意,恰有两个不同解
C.存在,有三个不同解
D.存在,无解
【答案】A
【解析】当时,,,
时,;时,,在上递减,在上递增,
,在上递增,又x大于0趋近于0时,也大于0趋近于0;
x趋近于正无穷时,也趋近于正无穷,又为R上的奇函数,其图象关于原点对称,
结合图象知,对任意的a,方程都恰有一解.故选:A.
2.【吉林省延边州2019届高三2月复检测】已知函数在上可导且,其导函数满足,对于函数,下列结论错误的是(
)
A.函数在上为单调递增函数
B.是函数的极小值点
C.函数至多有两个零点
D.时,不等式恒成立
【答案】D
若,则有2个零点,若,则函数有1个零点,
若,则函数没有零点,故正确;
由在递减,则在递减,
由,得时,,故,故,故错误,故选D.
3.已知函数的图像为上的一条连续不断的曲线,当时,,则关于的函数的零点的个数为(
)
A.0
B.1
C.2
D.0或2
【答案】A
4.【新疆乌鲁木齐市2019届高三一模】已知函数.
(Ⅰ)若的图像在点处的切线与直线平行,求的值;
(Ⅱ)若,讨论的零点个数.
【解析】(Ⅰ)函数,导数为,,
图象在点处的切线斜率为,由切线与直线平行,可得,解得;
(Ⅱ)若,可得,由,可得(舍去),即的零点个数为;
若,由,即为,可得,,设,,
当时,,递减;当时,,递增,
可得处取得极大值,且为最大值,
的图象如图:
由,即,可得和的图象只有一个交点,
即时,的零点个数为,综上可得在的零点个数为.
5.【辽宁省大连市2019届高三下学期第一次(3月)双基测试】已知函数f(x)=lnx+ax2-x(x>0,a∈R).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)求证:当a≤0时,曲线y=f(x)上任意一点处的切线与该曲线只有一个公共点.
【解析】
(Ⅰ)f′(x)=+2ax-1=(x>0),设g(x)=2ax2-x+1(x>0),
(1)当0<a<时,g(x)在(0,),(,+∞)上大于零,
在(,)上小于零,
所以f(x)在(0,),(,+∞)上递增,在(,)上递减,
(2)当a≥时,g(x)≥0(当且仅当a=,x=2时g(x)=0),所以f(x)在(0,+∞)上单调递增,
(3)当a=0时,g(x)在(0,1)上大于零,在(1,+∞)上小于零,
所以f(x)在(0,1)上单调递增,在(1,+∞)单调递减,
(4)当a<0时,g(x)在(0,)上大于零,在(,+∞)上小于零,
所以f(x)在(0,)上递增,在(,+∞)上递减;
(Ⅱ)曲线y=f(x)在点(t,f(t))处的曲线方程为:y=(+2at-1)(x-t)+lnt+at2-t,
曲线方程和y=f(x)联立可得:lnx+ax2-(+2at)x-lnt+at2+1=0,
设h(x)=lnx+ax2-(+2at)x-lnt+at2+1(x>0),h′(x)=,
当a≤0时,在(0,t)h′(x)>0,在(t,+∞)h′(x)<0,
故h(x)在(0,t)递增,在(t,+∞)递减,又h(t)=0,故h(x)只有唯一的零点t,
即切线与该曲线只有1个公共点(t,f(t)).
6.【四川省成都石室中学2019届高三第二次模拟】已知函数,.
(Ⅰ)当,函数图象上是否存在3条互相平行的切线,并说明理由?[]
(Ⅱ)讨论函数的零点个数.
【解析】
(Ⅰ),,,
则函数在单调递减,上单调递增,上单调递减,
因为,,,,,
所以存在切线斜率,
使得,,,,
所以函数图象上是存在3条互相平行的切线.
(Ⅱ),[]
当,有;,
在上单调递增;所以函数存在唯一一个零点在内;
当,有,;,
在上单调递增;所以函数存在唯一一个零点在内;
当,有,∴在上单调递增,在上单调递减,在上单调递增,,
,
,,,
所以函数一个零点在区间内,一个零点在区间内,一个零点在内.所以函数有三个不同零点.
综上所述:当函数一个零点;当函数三个零点.
7.【浙江省金华十校2019届高三上学期期末】已知,,其中,为自然对数的底数.
若函数的切线l经过点,求l的方程;
Ⅱ若函数在为递减函数,试判断函数零点的个数,并证明你的结论.
Ⅱ判断:函数的零点个数是0,下面证明恒成立,,故,
若在递减,则,因此,要证明对恒成立,
只需证明对恒成立,考虑等价于,
记,,先看,,
令,解得:,令,解得:,
故在递减,在递增,,
再看,.令,解得:,令,解得:,
故在递增,在递减,.
,且两个函数的极值点不在同一个x处,故对恒成立,
综上,对恒成立,故函数函数零点是0个.
8.【辽宁省丹东市2019届高三总复习质量测试(一)】已知函数.
(1)当时,讨论的单调性;(2)证明:当且时,只有一个零点.
【解析】(1).
当时,由得,由得,在单调递减,在单调递增.
当时,由得,由得或,在单调递减,在和单调递增.
令,,当时,,故在单调递增,所以,在单调递增,所以,因此.因为在单调递增,所以在有唯一零点.所以只有一个零点.
综上,当且时,只有一个零点.
9.【云南师范大学附属中学2019届高三上学期第一次月考】已知函数.
求的单调区间和极值;
当时,证明:对任意的,函数有且只有一个零点.
【解析】解:函数的定义域为,,
当时,,在定义域上单调递增,无极值;
当时,由,得,当时,,得的单调递增区间是;
当时,,得的单调递减区间是,
故的极大值为,无极小值.
由,得,当时,,则在上单调递增;
当时,,则在上单调递减,所以,
于是,则在上单调递减.
设,则,由,得,
当时,,则在上单调递减;
当时,,则在上单调递增,
所以,即当时,,
所以当时,,对任意的,有
当时,,有;
当时,有,
又在上单调递减,所以存在唯一的,有;
当时,,有,[]
当时,有,
又在上单调递减,所以存在唯一的,有,
综上所述,对任意的,方程有且只有一个正实数根,[]
即函数有且只有一个零点.
10.【2019届高三第一次全国大联考】已知函数(其中).
(1)当时,求函数的单调区间;(2)当时,求函数的极值点;
(3)讨论函数零点的个数.
(2)先考虑时的情况,
当时,则
;
所以当时,;当时,;
所以函数在上单调递减,在上单调递增.
又因为函数的图象关于直线对称,
所以在和上单调递减,在和上单调递增.
所以函数无极大值点,有2个极小值点,分别为和.
令,则
.
由,解得;由,解得,
所以在上递增,在上递减,所以,
当时,注意到,知此时在上单调递减,在上单调递增,且,这表明的图象与轴相切,
所以此时函数在上只有1个零点,且为;
当或时,,又当或时,,
所以此时函数在上有2个零点,一个零点是,另一个零点在区间或内.又由函数的图象关于直线对称,
综上可得,当或时,函数有2个零点;当或时,函数有4个零点.
11.【2019年四川省达州市高考一诊】已知,函数,.
求证:;讨论函数零点的个数.
,,,,
,方程有两个不相等的实根,分别为,
,且,,
当时,,递减,当时,,递增,
,,
,即,.
设,则,是减函数,
当,即时,,函数只有一个零点,
当,即时,,
函数没有零点,当,即时,,且,
由知,,
若,则有,,函数有且只有一个大于的零点,
又,即函数在区间有且只有一个零点,
综上,当时,函数有两个零点;当时,函数只有一个零点,
当时,函数没有零点.
12.【北京延庆区2019届高三一模】已知函数.
(1)当时,求曲线在点处的切线方程;
(2)求函数的单调区间;
(3)当时,求函数在上区间零点的个数.
【解析】(1)当时,,
,,,切点,所以切线方程是.
(2),
令,
、及的变化情况如下
0
增
减
所以,在区间上单调递增,在区间上单调递减.
(3)由(2)可知的最大值为,
(1)当时,在区间单调递增,在区间上单调递减.
由,故在区间上只有一个零点
.
(2)当时,,,,且
.
因为,所以,在区间上无零点.
综上,当时,在区间上只有一个零点,当时,在区间上无零点.
13.【广东省江门市2019届高考模拟(第一次模拟)】设函数,是自然对数的底数,是常数.(1)若,求的单调递增区间;
(2)讨论曲线与公共点的个数.
【答案】(1)的单调递增区间为(或);(2)或时,两曲线无公共点;或时,两曲线有一个公共点;时,两曲线有两个公共点
.
(I)时,有一个零点
.
(II)时,由解得,.当时,;当时,,
在取最小值
,
①时,,有一个零点.
②时,,无零点
.
③时,,由知,在有一个零点,即在有一个零点;由指数函数与幂函数单调性比较知,当且充分大时,,所以在有一个零点,即在有一个零点.从而有两个零点
.
(III)时,,单调递减,,,所以在有一个零点,从而在定义域内有一个零点
.
(IIII)时,无零点
.
14.【安徽省六安市毛坦厂中学2019届高三3月联考】设函数.
(1)试讨论函数的单调性;
(2)若,证明:方程有且仅有3个不同的实数根.(附:,,)[]
【解析】(1)由,得,
令,所以,
所以当时,,恒成立,即恒成立,所以单调递增;
即,所以单调递减;当时,,
即,所以单调递增.
综上,当时,在上单调递增;
当时,的单调递增区间为,;的单调递减区间为.
(2)当时,,由(1)知,函数在上单调递增,在上单调递减,在上单调递增,所以当时,函数有极大值,且
,
当时,函数有极小值,
且
.又因为,,所以直线与函数的图象在区间上有且仅有3个交点,
所以当时,方程有且仅有3个不同的实数根.
“四招”判断函数零点个数
函数方程思想是一种重要的数学思想方法,函数问题可以利用方程求解,方程解的情况可借助于函数的图象和性质求解.高考命题常常以基本初等函数为载体,主要考查以下三个方面:(1)零点所在区间——零点存在性定理;(2)二次方程根的分布问题;(3)判断零点的个数问题;(4)根据零点的情况确定参数的值或范围;(5)根据零点的情况讨论函数的性质或证明不等式等.本专题围绕函数零点个数的判断问题,例题说法,高效训练.
【典型例题】
第一招
应用函数性质,判定函数零点个数
例1.已知偶函数,且,则函数在区间的零点个数为(
)
A.
2020
B.
2016
C.
1010
D.
1008
【答案】A
【解析】
,
当时,函数与函数图象有个交点
,由知,
当时函数与函数图象有个交点
故函数的零点个数为,故选.
第二招
数形结合,判定函数零点个数
例2.【2018届福建省永春一中、培元、季延、石光中学四校高三上第二次联考】定义在上的函数满足,且时,
;
时,
.
令,则函数的零点个数为(
)
A.
B.
C.
D.
【答案】B
,
∵函数f(x)满足f(x+2)=f(x)+1,即自变量x每增加2个单位,函数图象向上平移1个单位,自变量每减少2个单位,函数图象向下平移1个单位,分别画出函数y=f(x)在x∈[﹣6,2],y=x+2的图象,
∴y=f(x)在x∈[﹣6,2],y=x+2有8个交点,故函数g(x)的零点个数为8个.故选:B.
第三招
应用零点存在性定理,判定函数零点个数
【广西桂林市、贺州市、崇左市2019届高三下学期3月联合调研】已知函数.(1)讨论的单调性;(2)讨论在上的零点个数.
∴当时,在上单调递增.
当时,在上单调递减,在上单调递增.
(2)设,则由(1)知
①当时,即,当时,,在单调递减
,
∴当,即,时,在上恒成立,
∴当时,在内无零点.
当,即,时,,
根据零点存在性定理知,此时,在内有零点,
∵在内单调递减,∴此时,在有一个零点.
②当时,即,当时,,在单调递增,
,.
∴当,即时,,根据零点存在性定理,此时,在内有零点.
∵在内单调递增,∴此时,在有一个零点.
当时,,∴此时,在无零点.
③当时,即,当时,;当时,;
则在单调递减,在单调递增.
∴在上恒成立,∴此时,在内无零点.
∴综上所述:当时,在内有1个零点;当时,在有一个零点;
当时,在无零点.
第四招
构造函数,判定函数零点个数
例4.【山东省菏泽市2019届高三上学期期末】已知函数f(x)=lnx+﹣1,a∈R.
(1)当a>0时,若函数f(x)在区间[1,3]上的最小值为,求a的值;
(2)讨论函数g(x)=f′(x)﹣零点的个数.
f’(x)min=f(a)=lna,令,得.
当a≥3时,f’(x)<0在(1,3)上恒成立,这时f(x)在[1,3]上为减函数,
∴,令得a=4﹣3ln3<2(舍去).
综上知.
(2)∵函数,
令g(x)=0,得.
设,,
当x∈(0,1)时,φ'(x)>0,此时φ(x)在(0,1)上单调递增,
当x∈(1,+∞)时,φ’(x)<0,此时φ(x)在(1,+∞)上单调递减,
所以x=1是φ(x)的唯一极值点,且是极大值点,因此x=1也是(x)的最大值点,
φ(x)的最大值为.
又φ(0)=0,结合φ(x)的图象可知:
①当时,函数g(x)无零点;
②当时,函数g(x)有且仅有一个零点;
③当时,函数g(x)有两个零点;
④a≤0时,函数g(x)有且只有一个零点;
综上所述,当时,函数g(x)无零点;当或a≤0时,函数g(x)有且仅有一个零点;
当时,函数g(x)有两个零点.
【规律与方法】
函数零点个数的求解与判断:
(1)直接求零点:令,如果能求出解,则有几个解就有几个零点;
(2)零点存在性定理:利用定理不仅要函数在区间上是连续不断的曲线,且,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点;
(3)利用图象交点的个数:将函数变形为两个函数的差,画两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点.
(4)构造函数模型,判断零点个数.构造函数可根据题目不同,直接做差构造函数、分离参数后构造函数、先求导数再构造函数、先换元再构造函数等.
【提升训练】
1.【浙江省杭州地区(含周边)重点中学2019届高三上期中】已知定义在R上的奇函数,满足当时,则关于x的方程满足
A.对任意,恰有一解
B.对任意,恰有两个不同解
C.存在,有三个不同解
D.存在,无解
【答案】A
【解析】当时,,,
时,;时,,在上递减,在上递增,
,在上递增,又x大于0趋近于0时,也大于0趋近于0;
x趋近于正无穷时,也趋近于正无穷,又为R上的奇函数,其图象关于原点对称,
结合图象知,对任意的a,方程都恰有一解.故选:A.
2.【吉林省延边州2019届高三2月复检测】已知函数在上可导且,其导函数满足,对于函数,下列结论错误的是(
)
A.函数在上为单调递增函数
B.是函数的极小值点
C.函数至多有两个零点
D.时,不等式恒成立
【答案】D
若,则有2个零点,若,则函数有1个零点,
若,则函数没有零点,故正确;
由在递减,则在递减,
由,得时,,故,故,故错误,故选D.
3.已知函数的图像为上的一条连续不断的曲线,当时,,则关于的函数的零点的个数为(
)
A.0
B.1
C.2
D.0或2
【答案】A
4.【新疆乌鲁木齐市2019届高三一模】已知函数.
(Ⅰ)若的图像在点处的切线与直线平行,求的值;
(Ⅱ)若,讨论的零点个数.
【解析】(Ⅰ)函数,导数为,,
图象在点处的切线斜率为,由切线与直线平行,可得,解得;
(Ⅱ)若,可得,由,可得(舍去),即的零点个数为;
若,由,即为,可得,,设,,
当时,,递减;当时,,递增,
可得处取得极大值,且为最大值,
的图象如图:
由,即,可得和的图象只有一个交点,
即时,的零点个数为,综上可得在的零点个数为.
5.【辽宁省大连市2019届高三下学期第一次(3月)双基测试】已知函数f(x)=lnx+ax2-x(x>0,a∈R).
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)求证:当a≤0时,曲线y=f(x)上任意一点处的切线与该曲线只有一个公共点.
【解析】
(Ⅰ)f′(x)=+2ax-1=(x>0),设g(x)=2ax2-x+1(x>0),
(1)当0<a<时,g(x)在(0,),(,+∞)上大于零,
在(,)上小于零,
所以f(x)在(0,),(,+∞)上递增,在(,)上递减,
(2)当a≥时,g(x)≥0(当且仅当a=,x=2时g(x)=0),所以f(x)在(0,+∞)上单调递增,
(3)当a=0时,g(x)在(0,1)上大于零,在(1,+∞)上小于零,
所以f(x)在(0,1)上单调递增,在(1,+∞)单调递减,
(4)当a<0时,g(x)在(0,)上大于零,在(,+∞)上小于零,
所以f(x)在(0,)上递增,在(,+∞)上递减;
(Ⅱ)曲线y=f(x)在点(t,f(t))处的曲线方程为:y=(+2at-1)(x-t)+lnt+at2-t,
曲线方程和y=f(x)联立可得:lnx+ax2-(+2at)x-lnt+at2+1=0,
设h(x)=lnx+ax2-(+2at)x-lnt+at2+1(x>0),h′(x)=,
当a≤0时,在(0,t)h′(x)>0,在(t,+∞)h′(x)<0,
故h(x)在(0,t)递增,在(t,+∞)递减,又h(t)=0,故h(x)只有唯一的零点t,
即切线与该曲线只有1个公共点(t,f(t)).
6.【四川省成都石室中学2019届高三第二次模拟】已知函数,.
(Ⅰ)当,函数图象上是否存在3条互相平行的切线,并说明理由?[]
(Ⅱ)讨论函数的零点个数.
【解析】
(Ⅰ),,,
则函数在单调递减,上单调递增,上单调递减,
因为,,,,,
所以存在切线斜率,
使得,,,,
所以函数图象上是存在3条互相平行的切线.
(Ⅱ),[]
当,有;,
在上单调递增;所以函数存在唯一一个零点在内;
当,有,;,
在上单调递增;所以函数存在唯一一个零点在内;
当,有,∴在上单调递增,在上单调递减,在上单调递增,,
,
,,,
所以函数一个零点在区间内,一个零点在区间内,一个零点在内.所以函数有三个不同零点.
综上所述:当函数一个零点;当函数三个零点.
7.【浙江省金华十校2019届高三上学期期末】已知,,其中,为自然对数的底数.
若函数的切线l经过点,求l的方程;
Ⅱ若函数在为递减函数,试判断函数零点的个数,并证明你的结论.
Ⅱ判断:函数的零点个数是0,下面证明恒成立,,故,
若在递减,则,因此,要证明对恒成立,
只需证明对恒成立,考虑等价于,
记,,先看,,
令,解得:,令,解得:,
故在递减,在递增,,
再看,.令,解得:,令,解得:,
故在递增,在递减,.
,且两个函数的极值点不在同一个x处,故对恒成立,
综上,对恒成立,故函数函数零点是0个.
8.【辽宁省丹东市2019届高三总复习质量测试(一)】已知函数.
(1)当时,讨论的单调性;(2)证明:当且时,只有一个零点.
【解析】(1).
当时,由得,由得,在单调递减,在单调递增.
当时,由得,由得或,在单调递减,在和单调递增.
令,,当时,,故在单调递增,所以,在单调递增,所以,因此.因为在单调递增,所以在有唯一零点.所以只有一个零点.
综上,当且时,只有一个零点.
9.【云南师范大学附属中学2019届高三上学期第一次月考】已知函数.
求的单调区间和极值;
当时,证明:对任意的,函数有且只有一个零点.
【解析】解:函数的定义域为,,
当时,,在定义域上单调递增,无极值;
当时,由,得,当时,,得的单调递增区间是;
当时,,得的单调递减区间是,
故的极大值为,无极小值.
由,得,当时,,则在上单调递增;
当时,,则在上单调递减,所以,
于是,则在上单调递减.
设,则,由,得,
当时,,则在上单调递减;
当时,,则在上单调递增,
所以,即当时,,
所以当时,,对任意的,有
当时,,有;
当时,有,
又在上单调递减,所以存在唯一的,有;
当时,,有,[]
当时,有,
又在上单调递减,所以存在唯一的,有,
综上所述,对任意的,方程有且只有一个正实数根,[]
即函数有且只有一个零点.
10.【2019届高三第一次全国大联考】已知函数(其中).
(1)当时,求函数的单调区间;(2)当时,求函数的极值点;
(3)讨论函数零点的个数.
(2)先考虑时的情况,
当时,则
;
所以当时,;当时,;
所以函数在上单调递减,在上单调递增.
又因为函数的图象关于直线对称,
所以在和上单调递减,在和上单调递增.
所以函数无极大值点,有2个极小值点,分别为和.
令,则
.
由,解得;由,解得,
所以在上递增,在上递减,所以,
当时,注意到,知此时在上单调递减,在上单调递增,且,这表明的图象与轴相切,
所以此时函数在上只有1个零点,且为;
当或时,,又当或时,,
所以此时函数在上有2个零点,一个零点是,另一个零点在区间或内.又由函数的图象关于直线对称,
综上可得,当或时,函数有2个零点;当或时,函数有4个零点.
11.【2019年四川省达州市高考一诊】已知,函数,.
求证:;讨论函数零点的个数.
,,,,
,方程有两个不相等的实根,分别为,
,且,,
当时,,递减,当时,,递增,
,,
,即,.
设,则,是减函数,
当,即时,,函数只有一个零点,
当,即时,,
函数没有零点,当,即时,,且,
由知,,
若,则有,,函数有且只有一个大于的零点,
又,即函数在区间有且只有一个零点,
综上,当时,函数有两个零点;当时,函数只有一个零点,
当时,函数没有零点.
12.【北京延庆区2019届高三一模】已知函数.
(1)当时,求曲线在点处的切线方程;
(2)求函数的单调区间;
(3)当时,求函数在上区间零点的个数.
【解析】(1)当时,,
,,,切点,所以切线方程是.
(2),
令,
、及的变化情况如下
0
增
减
所以,在区间上单调递增,在区间上单调递减.
(3)由(2)可知的最大值为,
(1)当时,在区间单调递增,在区间上单调递减.
由,故在区间上只有一个零点
.
(2)当时,,,,且
.
因为,所以,在区间上无零点.
综上,当时,在区间上只有一个零点,当时,在区间上无零点.
13.【广东省江门市2019届高考模拟(第一次模拟)】设函数,是自然对数的底数,是常数.(1)若,求的单调递增区间;
(2)讨论曲线与公共点的个数.
【答案】(1)的单调递增区间为(或);(2)或时,两曲线无公共点;或时,两曲线有一个公共点;时,两曲线有两个公共点
.
(I)时,有一个零点
.
(II)时,由解得,.当时,;当时,,
在取最小值
,
①时,,有一个零点.
②时,,无零点
.
③时,,由知,在有一个零点,即在有一个零点;由指数函数与幂函数单调性比较知,当且充分大时,,所以在有一个零点,即在有一个零点.从而有两个零点
.
(III)时,,单调递减,,,所以在有一个零点,从而在定义域内有一个零点
.
(IIII)时,无零点
.
14.【安徽省六安市毛坦厂中学2019届高三3月联考】设函数.
(1)试讨论函数的单调性;
(2)若,证明:方程有且仅有3个不同的实数根.(附:,,)[]
【解析】(1)由,得,
令,所以,
所以当时,,恒成立,即恒成立,所以单调递增;
即,所以单调递减;当时,,
即,所以单调递增.
综上,当时,在上单调递增;
当时,的单调递增区间为,;的单调递减区间为.
(2)当时,,由(1)知,函数在上单调递增,在上单调递减,在上单调递增,所以当时,函数有极大值,且
,
当时,函数有极小值,
且
.又因为,,所以直线与函数的图象在区间上有且仅有3个交点,
所以当时,方程有且仅有3个不同的实数根.
同课章节目录
