A典学案 第19课时 第三章 圆的对称性 习题课件
文档属性
| 名称 | A典学案 第19课时 第三章 圆的对称性 习题课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-01 09:14:33 | ||
图片预览



文档简介
课件9张PPT。第三章 圆 第 19 课时 圆的对称性北师大版 九年级下册类型之一 :弧、弦、圆心角之间的关系
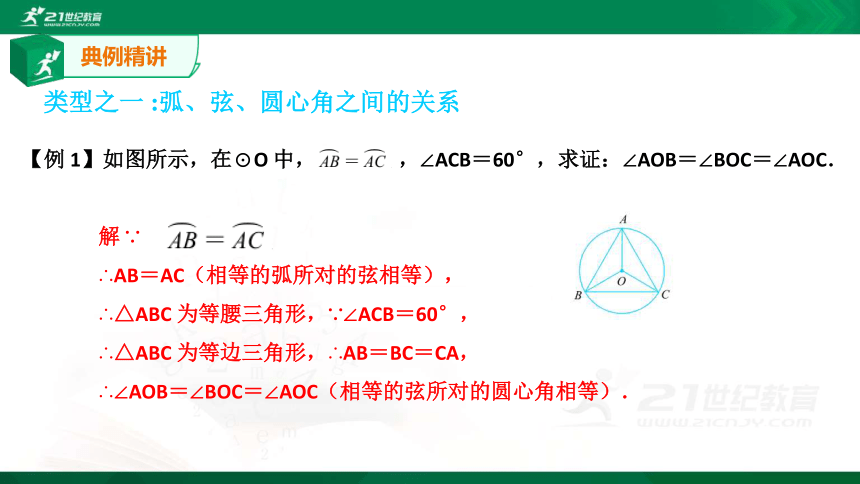
典例精讲【例 1】如图所示,在⊙O 中, ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.解 ∵
∴AB=AC(相等的弧所对的弦相等),
∴△ABC 为等腰三角形,∵∠ACB=60°,
∴△ABC 为等边三角形,∴AB=BC=CA,
∴∠AOB=∠BOC=∠AOC(相等的弦所对的圆心角相等).类型之一 :弧、弦、圆心角之间的关系
典例精讲【例 2】如图所示,已知 AB,CD 是⊙O 的两条直径,AP 是⊙O 的弦,且 AP∥CD,∠A=70°,那么 相等吗?说明你的理由.如果∠A=α,该结论成立吗?解:相等,理由如下:连接 OP,
∵OA=OP,∴∠OAP=∠OPA=70°,
∵AP∥CD,
∴∠BOD=∠OAP=70°,∠POD=∠APO=70°,
当∠A=α 时,该结论仍然成立,证明过程同上.∴∠POD=∠BOD,∴ ? = ? .类型之二:利用弧、弦、圆心角之间的关系进行证明典例精讲【例 3】如图所示,已知 AB 是⊙O 的直径,M,N 分别是 AO,BO 的中点,CM⊥
AB,DN⊥AB.求证: ?解:连接 OC,OD,
∵AB 是⊙O 的直径,M,N 分别是 AO,BO 的中点,
∴OM=ON,∵CM⊥AB,DN⊥AB,
∴∠OMC=∠OND=90°,
在 Rt△OMC 和 Rt△OND 中,
∴Rt△OMC≌Rt△OND(HL),∴∠COM=∠DON,课堂操练AB1.下列图形中的角是圆心角的是( )
2.同圆中的两条弦长为 m1 和 m2 ,圆心到两条弦的距离分别为 d1和 d2 ,且 d1 >d2 ,那么 m1 , m2 的大小关系是( )
A. m1 > m2 B. m1 < m2 C. m1 = m2 D. m1 ≤ m2课堂操练30°403.如图所示,已知 BD 是⊙O 的直径,点 A,C 在⊙O 上, ,∠ABO=60°,则∠DCO 的度数是 .
4.如图所示,在⊙O 中,点 C 是 ? 的中点,∠A=50°,则∠BOC 等于 °.课堂操练5.如图所示,在△AOB 中,AO=AB,以点 O 为圆心,OB 为半径的圆交 AB 于 D,交AO 于点 E,AD=BO.试说明 ? ,并求∠A 的度数.解:设∠A=x,
∵AD=OB,∴DO=DA,
∴∠DOA=x,∴∠BDO=2x,∴∠B=2x,
又∵AO=AB,∴∠BOE=∠B=2x,
∴∠BOD=2x-x=x=∠DOE,
在△OBD 中,x+2x+2x=180°,∴x=36°,
即∠A=36°.谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
典例精讲【例 1】如图所示,在⊙O 中, ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.解 ∵
∴AB=AC(相等的弧所对的弦相等),
∴△ABC 为等腰三角形,∵∠ACB=60°,
∴△ABC 为等边三角形,∴AB=BC=CA,
∴∠AOB=∠BOC=∠AOC(相等的弦所对的圆心角相等).类型之一 :弧、弦、圆心角之间的关系
典例精讲【例 2】如图所示,已知 AB,CD 是⊙O 的两条直径,AP 是⊙O 的弦,且 AP∥CD,∠A=70°,那么 相等吗?说明你的理由.如果∠A=α,该结论成立吗?解:相等,理由如下:连接 OP,
∵OA=OP,∴∠OAP=∠OPA=70°,
∵AP∥CD,
∴∠BOD=∠OAP=70°,∠POD=∠APO=70°,
当∠A=α 时,该结论仍然成立,证明过程同上.∴∠POD=∠BOD,∴ ? = ? .类型之二:利用弧、弦、圆心角之间的关系进行证明典例精讲【例 3】如图所示,已知 AB 是⊙O 的直径,M,N 分别是 AO,BO 的中点,CM⊥
AB,DN⊥AB.求证: ?解:连接 OC,OD,
∵AB 是⊙O 的直径,M,N 分别是 AO,BO 的中点,
∴OM=ON,∵CM⊥AB,DN⊥AB,
∴∠OMC=∠OND=90°,
在 Rt△OMC 和 Rt△OND 中,
∴Rt△OMC≌Rt△OND(HL),∴∠COM=∠DON,课堂操练AB1.下列图形中的角是圆心角的是( )
2.同圆中的两条弦长为 m1 和 m2 ,圆心到两条弦的距离分别为 d1和 d2 ,且 d1 >d2 ,那么 m1 , m2 的大小关系是( )
A. m1 > m2 B. m1 < m2 C. m1 = m2 D. m1 ≤ m2课堂操练30°403.如图所示,已知 BD 是⊙O 的直径,点 A,C 在⊙O 上, ,∠ABO=60°,则∠DCO 的度数是 .
4.如图所示,在⊙O 中,点 C 是 ? 的中点,∠A=50°,则∠BOC 等于 °.课堂操练5.如图所示,在△AOB 中,AO=AB,以点 O 为圆心,OB 为半径的圆交 AB 于 D,交AO 于点 E,AD=BO.试说明 ? ,并求∠A 的度数.解:设∠A=x,
∵AD=OB,∴DO=DA,
∴∠DOA=x,∴∠BDO=2x,∴∠B=2x,
又∵AO=AB,∴∠BOE=∠B=2x,
∴∠BOD=2x-x=x=∠DOE,
在△OBD 中,x+2x+2x=180°,∴x=36°,
即∠A=36°.谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
