A典学案 第21课时 第三章 圆心角和圆心角的关系(1) 习题课件
文档属性
| 名称 | A典学案 第21课时 第三章 圆心角和圆心角的关系(1) 习题课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-01 09:54:55 | ||
图片预览




文档简介
课件10张PPT。第三章 圆 圆心角和圆心角的关系(1)北师大版 九年级下册类型之一 :圆周角定理的基本运用典例精讲【例 1】如图所示,点 A,B,C 都在⊙O 上,若∠O=60°,则∠C 的度数为( )
A.20°
B.25°
C.30°
D.45°C类型之一 :圆周角定理的基本运用典例精讲【例 2】如图所示,已知⊙O 中,弦 AB 的长等于⊙O 的半径,求弦 AB 所对的圆心角和圆周角的度数.解:连接 OA,OB,
∵AB=OA=OB,
∴△OAB 为等边三角形,
∴弦 AB 所对的圆心角∠AOB=60°,
弦 AB 所对的圆周角分两种情况:
30°(角顶点在优弧)或 150°(角顶点在劣弧).类型之二 :圆周角定理的综合运用典例精讲【例 3】如图所示,⊙O 的弦 AB,CD 的延长线相交于点 M,弦 AD,BD 相交于点E,若 ? 所对的圆心角为 72°, 所对的圆心角为 18°.求∠M+∠AEC 的值.∴∠A=∠C=9°,∠ABC=36°,
∴∠M=∠ABC-∠C=27°,∠AEC=∠A+∠ABC=45°,
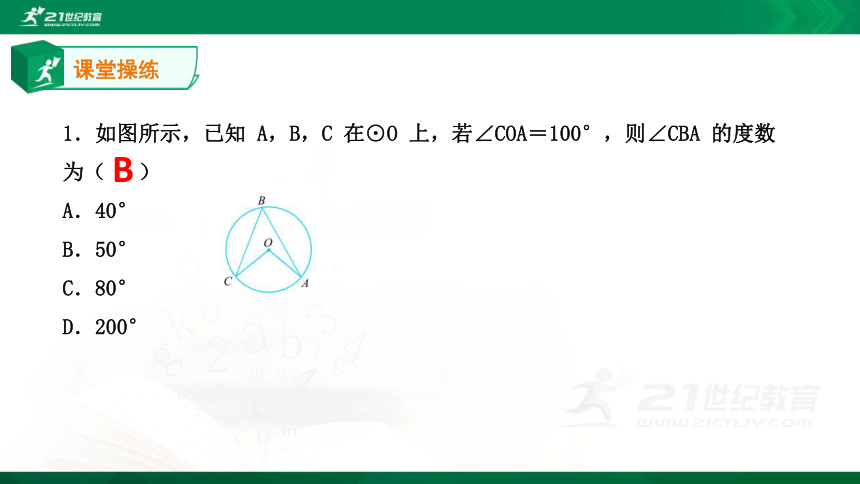
∴∠M+∠AEC=72°.解∵ ? 所对的圆心角为 72°, ? 所对应的圆心角为 18°,课堂操练B1.如图所示,已知 A,B,C 在⊙O 上,若∠COA=100°,则∠CBA 的度数为( )
A.40°
B.50°
C.80°
D.200° 课堂操练D2.如图所示,AC 是⊙O 的直径,AB,CD 是⊙O 的两条弦,且 AB∥CD.如果∠BAC=32°,则∠AOD 的度数是( )
A.16° B.32° C.48° D.64° 课堂操练50°93.如图所示,在⊙O 中,∠ACB=∠D=60°,AC=3,则△ABC 的周长为 .
4.如图所示,⊙O 中 OA⊥BC,∠CDA=25°,则∠AOB 的度数为 .5.如图所示,点 A,B,C,D 都在⊙O 上,OC⊥AB,∠ADC=30°.求∠BOC 的度数.解∵点 A,B,C,D 都在⊙O 上,OC⊥AB,
∵∠ADC=30°,
∴∠AOC=∠BOC=2∠ADC=60°,
∴∠BOC 的度数为 60°.课堂操练谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
A.20°
B.25°
C.30°
D.45°C类型之一 :圆周角定理的基本运用典例精讲【例 2】如图所示,已知⊙O 中,弦 AB 的长等于⊙O 的半径,求弦 AB 所对的圆心角和圆周角的度数.解:连接 OA,OB,
∵AB=OA=OB,
∴△OAB 为等边三角形,
∴弦 AB 所对的圆心角∠AOB=60°,
弦 AB 所对的圆周角分两种情况:
30°(角顶点在优弧)或 150°(角顶点在劣弧).类型之二 :圆周角定理的综合运用典例精讲【例 3】如图所示,⊙O 的弦 AB,CD 的延长线相交于点 M,弦 AD,BD 相交于点E,若 ? 所对的圆心角为 72°, 所对的圆心角为 18°.求∠M+∠AEC 的值.∴∠A=∠C=9°,∠ABC=36°,
∴∠M=∠ABC-∠C=27°,∠AEC=∠A+∠ABC=45°,
∴∠M+∠AEC=72°.解∵ ? 所对的圆心角为 72°, ? 所对应的圆心角为 18°,课堂操练B1.如图所示,已知 A,B,C 在⊙O 上,若∠COA=100°,则∠CBA 的度数为( )
A.40°
B.50°
C.80°
D.200° 课堂操练D2.如图所示,AC 是⊙O 的直径,AB,CD 是⊙O 的两条弦,且 AB∥CD.如果∠BAC=32°,则∠AOD 的度数是( )
A.16° B.32° C.48° D.64° 课堂操练50°93.如图所示,在⊙O 中,∠ACB=∠D=60°,AC=3,则△ABC 的周长为 .
4.如图所示,⊙O 中 OA⊥BC,∠CDA=25°,则∠AOB 的度数为 .5.如图所示,点 A,B,C,D 都在⊙O 上,OC⊥AB,∠ADC=30°.求∠BOC 的度数.解∵点 A,B,C,D 都在⊙O 上,OC⊥AB,
∵∠ADC=30°,
∴∠AOC=∠BOC=2∠ADC=60°,
∴∠BOC 的度数为 60°.课堂操练谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
