3.1.1方程的根与函数的零点 课件
文档属性
| 名称 | 3.1.1方程的根与函数的零点 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-01 16:57:39 | ||
图片预览




文档简介
(共24张PPT)
【教学目标】
学习目标:1、 一元二次方程的根及其相应二次函数的图象与x轴交点的关系;2、函数零点的概念3、函数零点与方程的根的关系.4、函数零点存在性定理
能力目标:培养学生数形结合的思想和联系的思想
【重点、难点】
重点:1.函数零点的概念;2.函数零点与方程的根的关系.
3.函数零点存在性定理
难点及关键:1、弄清函数、方程和零点的关系2、灵活应用函数零点存在性定理
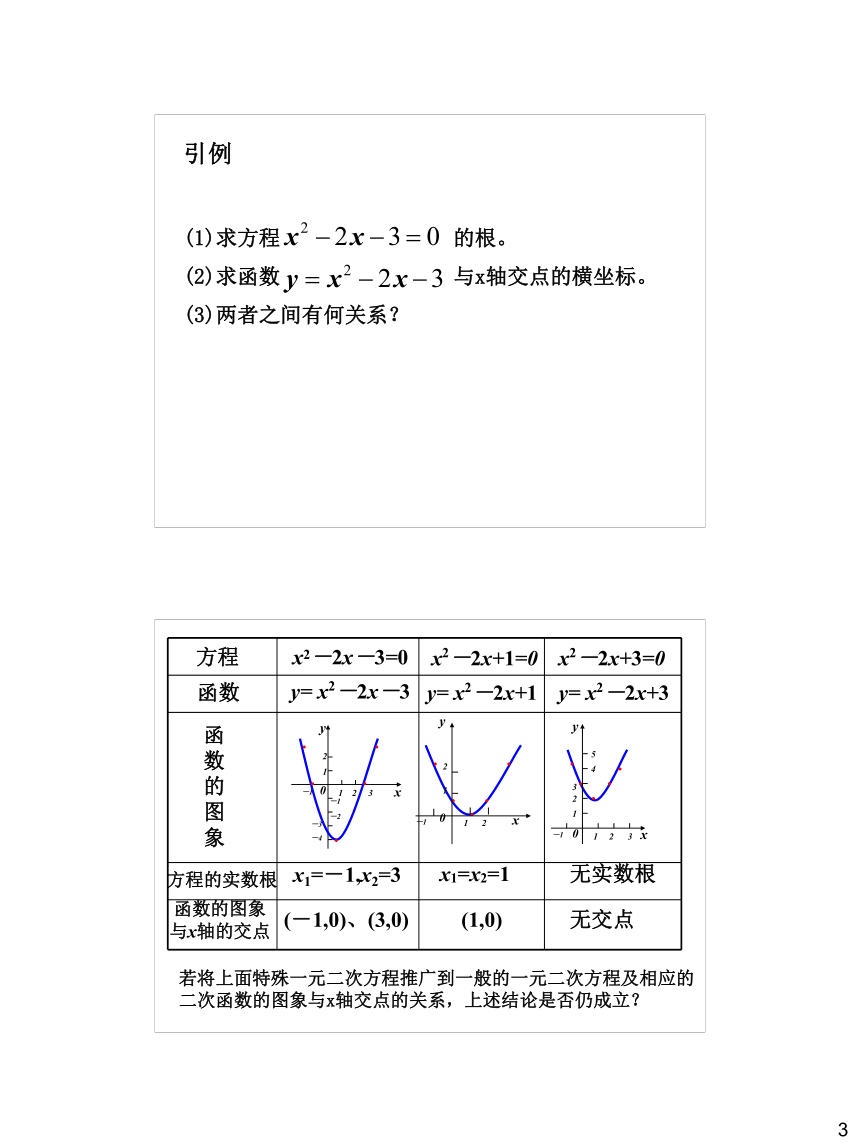
引例
求方程 的根。
求函数 与x轴交点的横坐标。
两者之间有何关系?
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
y= x2-2x+3
若将上面特殊一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍成立?
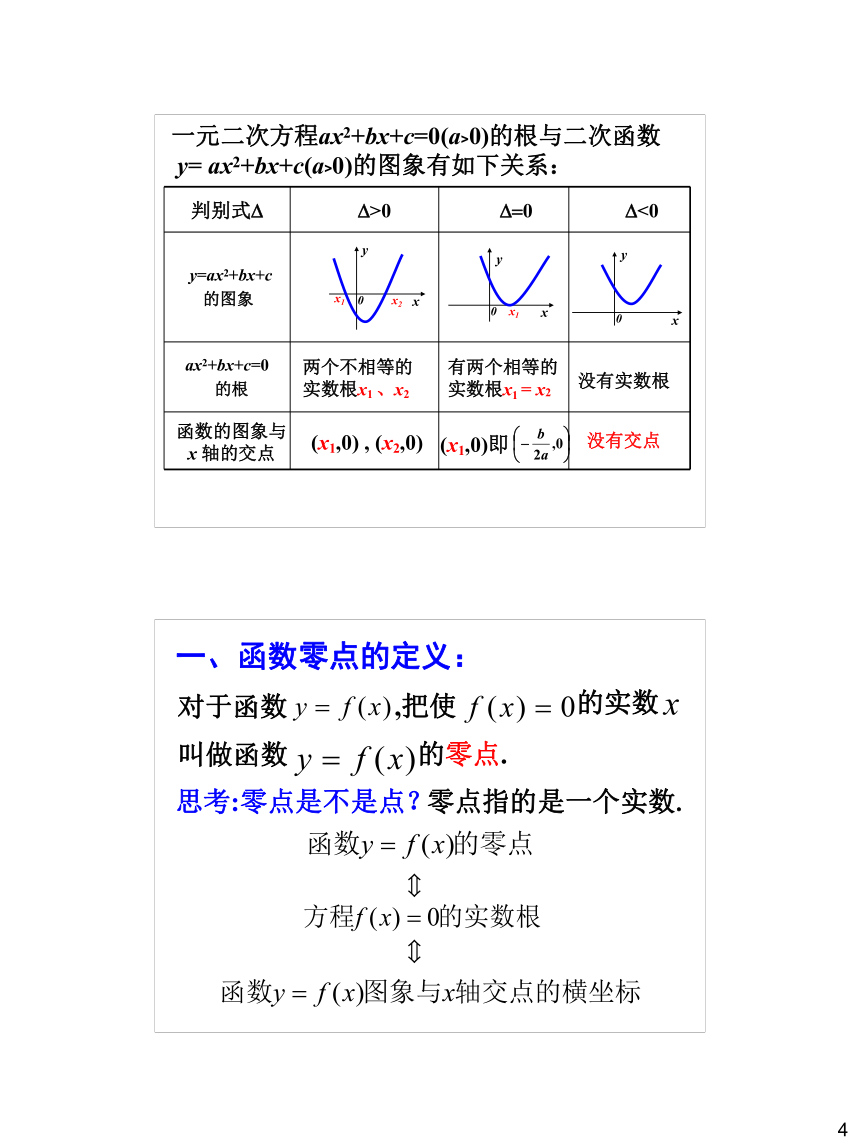
一元二次方程ax2+bx+c=0(a>0)的根与二次函数
y= ax2+bx+c(a>0)的图象有如下关系:
函数的图象与
x 轴的交点
(x1,0) , (x2,0)
没有交点
有两个相等的实数根x1 = x2
没有实数根
两个不相等的实数根x1 、x2
(x1,0)即
判别式? ?>0 ??0 ?<0
y=ax2+bx+c
的图象
ax2+bx+c=0
的根
一、函数零点的定义:
思考:零点是不是点?
零点指的是一个实数.
求下列函数的零点:
变式1:
函数f(x)=Lnx+2x-6在[2,6]上是否有零点?
观察二次函数f(x)=x2-2x-3图象
<
5
-4
-1
<
3
-3
5
-2
1. 在区间(a,b)上____(有/无)零点;
f(a)·f(b) ____ 0(填<或>).
2 .在区间(b,c)上____(有/无)零点;
f(b)· f(c)____ 0(填<或>).
思考:函数在区间端点上的函数值的符号情况,与
函数零点是否存在某种关系?
猜想:
若函数在区间[a,b]上图象是连续的,如果有 成立,
那么函数在区间(a,b)上有零点。
观察函数f(x)的图像
0
y
x
有
<
有
<
f(a)·f(b)< 0
二、函数零点存在性定理:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。
即存在 c∈(a,b) ,使得 f(c) =0, 这个c也就是方程 f(x)=0 的根。
(1) f(a)·f(b)<0则函数y=f(x)在区间(a,b)内有零点。
(2) 函数y=f(x)在区间(a,b)内零点,则f(a)·f(b)<0。
(3) f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内只有一个零点。
函数零点存在定理的三个注意点:
1 函数是连续的。
2 定理不可逆。
3 至少存在一个零点。
定理理解:判断正误
错
错
错
函数 在下列哪个区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
C
解析:
例1:求函数 的零点个数?
例1:求函数 的零点个数.
解法2:
练习2:方程 在下列哪个区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
C
解法二:
三、求函数零点或零点个数的方法:
(1)定义法:解方程 f(x)=0,
得出函数的零点。
(2)图象法:画出y= f(x)的图象,其图象与x轴交点的横坐标。
(3)定理法:函数零点存在性定理。
练习3:下列函数在区间(1,2)上有零点的是( )
(A) f(x)=3x2-4x+5 (B) f(x)=x?-5x-5
(C) f(x)=lnx-3x+6 (D) f(x)=ex+3x-6
练习4:f(x)=x3+x-1在下列哪个区间上有
零点( )
A.(-2,-1) B.(0,1) C.(1,2) D.(2,3)
D
B
【总一总★成竹在胸】
一元二次方程的根及其相应
二次函数的图象与x轴交点的关系;
函数零点的概念;
函数零点与方程的根的关系.
函数零点存在性定理
课后作业:
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
【教学目标】
学习目标:1、 一元二次方程的根及其相应二次函数的图象与x轴交点的关系;2、函数零点的概念3、函数零点与方程的根的关系.4、函数零点存在性定理
能力目标:培养学生数形结合的思想和联系的思想
【重点、难点】
重点:1.函数零点的概念;2.函数零点与方程的根的关系.
3.函数零点存在性定理
难点及关键:1、弄清函数、方程和零点的关系2、灵活应用函数零点存在性定理
引例
求方程 的根。
求函数 与x轴交点的横坐标。
两者之间有何关系?
方程
x2-2x+1=0
x2-2x+3=0
y= x2-2x-3
y= x2-2x+1
函数
函
数
的
图
象
方程的实数根
x1=-1,x2=3
x1=x2=1
无实数根
函数的图象
与x轴的交点
(-1,0)、(3,0)
(1,0)
无交点
x2-2x-3=0
y= x2-2x+3
若将上面特殊一元二次方程推广到一般的一元二次方程及相应的二次函数的图象与x轴交点的关系,上述结论是否仍成立?
一元二次方程ax2+bx+c=0(a>0)的根与二次函数
y= ax2+bx+c(a>0)的图象有如下关系:
函数的图象与
x 轴的交点
(x1,0) , (x2,0)
没有交点
有两个相等的实数根x1 = x2
没有实数根
两个不相等的实数根x1 、x2
(x1,0)即
判别式? ?>0 ??0 ?<0
y=ax2+bx+c
的图象
ax2+bx+c=0
的根
一、函数零点的定义:
思考:零点是不是点?
零点指的是一个实数.
求下列函数的零点:
变式1:
函数f(x)=Lnx+2x-6在[2,6]上是否有零点?
观察二次函数f(x)=x2-2x-3图象
<
5
-4
-1
<
3
-3
5
-2
1. 在区间(a,b)上____(有/无)零点;
f(a)·f(b) ____ 0(填<或>).
2 .在区间(b,c)上____(有/无)零点;
f(b)· f(c)____ 0(填<或>).
思考:函数在区间端点上的函数值的符号情况,与
函数零点是否存在某种关系?
猜想:
若函数在区间[a,b]上图象是连续的,如果有 成立,
那么函数在区间(a,b)上有零点。
观察函数f(x)的图像
0
y
x
有
<
有
<
f(a)·f(b)< 0
二、函数零点存在性定理:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。
即存在 c∈(a,b) ,使得 f(c) =0, 这个c也就是方程 f(x)=0 的根。
(1) f(a)·f(b)<0则函数y=f(x)在区间(a,b)内有零点。
(2) 函数y=f(x)在区间(a,b)内零点,则f(a)·f(b)<0。
(3) f(a)·f(b)<0,则函数y=f(x)在区间(a,b)内只有一个零点。
函数零点存在定理的三个注意点:
1 函数是连续的。
2 定理不可逆。
3 至少存在一个零点。
定理理解:判断正误
错
错
错
函数 在下列哪个区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
C
解析:
例1:求函数 的零点个数?
例1:求函数 的零点个数.
解法2:
练习2:方程 在下列哪个区间上有零点( )
A.(0,1) B.(1,2) C.(2,3) D.(3,4)
C
解法二:
三、求函数零点或零点个数的方法:
(1)定义法:解方程 f(x)=0,
得出函数的零点。
(2)图象法:画出y= f(x)的图象,其图象与x轴交点的横坐标。
(3)定理法:函数零点存在性定理。
练习3:下列函数在区间(1,2)上有零点的是( )
(A) f(x)=3x2-4x+5 (B) f(x)=x?-5x-5
(C) f(x)=lnx-3x+6 (D) f(x)=ex+3x-6
练习4:f(x)=x3+x-1在下列哪个区间上有
零点( )
A.(-2,-1) B.(0,1) C.(1,2) D.(2,3)
D
B
【总一总★成竹在胸】
一元二次方程的根及其相应
二次函数的图象与x轴交点的关系;
函数零点的概念;
函数零点与方程的根的关系.
函数零点存在性定理
课后作业:
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
