13.2.4 三角形的外角学案(要点讲解+当堂检测+答案)
文档属性
| 名称 | 13.2.4 三角形的外角学案(要点讲解+当堂检测+答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-01 16:21:07 | ||
图片预览

文档简介
沪科版数学八年级上册同步学案
第13章 三角形中的边角关系、命题与证明
13.2 命题与证明
13.2.4 三角形的外角
要 点 讲 解
要点一 三角形的外角的定义
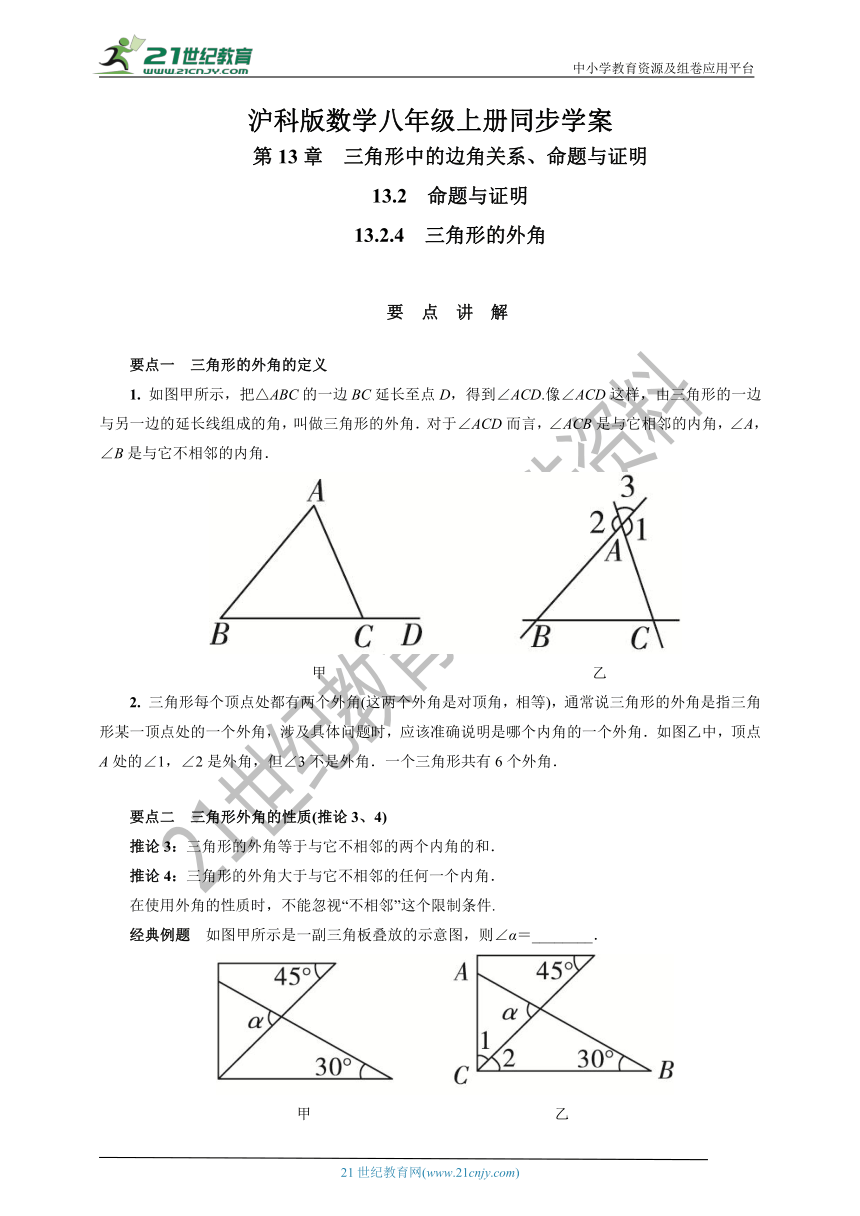
1. 如图甲所示,把△ABC的一边BC延长至点D,得到∠ACD.像∠ACD这样,由三角形的一边与另一边的延长线组成的角,叫做三角形的外角.对于∠ACD而言,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
甲 乙
2. 三角形每个顶点处都有两个外角(这两个外角是对顶角,相等),通常说三角形的外角是指三角形某一顶点处的一个外角,涉及具体问题时,应该准确说明是哪个内角的一个外角.如图乙中,顶点A处的∠1,∠2是外角,但∠3不是外角.一个三角形共有6个外角.
要点二 三角形外角的性质(推论3、4)
推论3:三角形的外角等于与它不相邻的两个内角的和.
推论4:三角形的外角大于与它不相邻的任何一个内角.
在使用外角的性质时,不能忽视“不相邻”这个限制条件.
经典例题 如图甲所示是一副三角板叠放的示意图,则∠α=________.
甲 乙
解析:如图乙所示.
∵∠ACB=90°,∠1=45°,∴∠2=90°-45°=45°,
∴∠α=∠2+∠B=45°+30°=75°.
答案:75°
当 堂 检 测
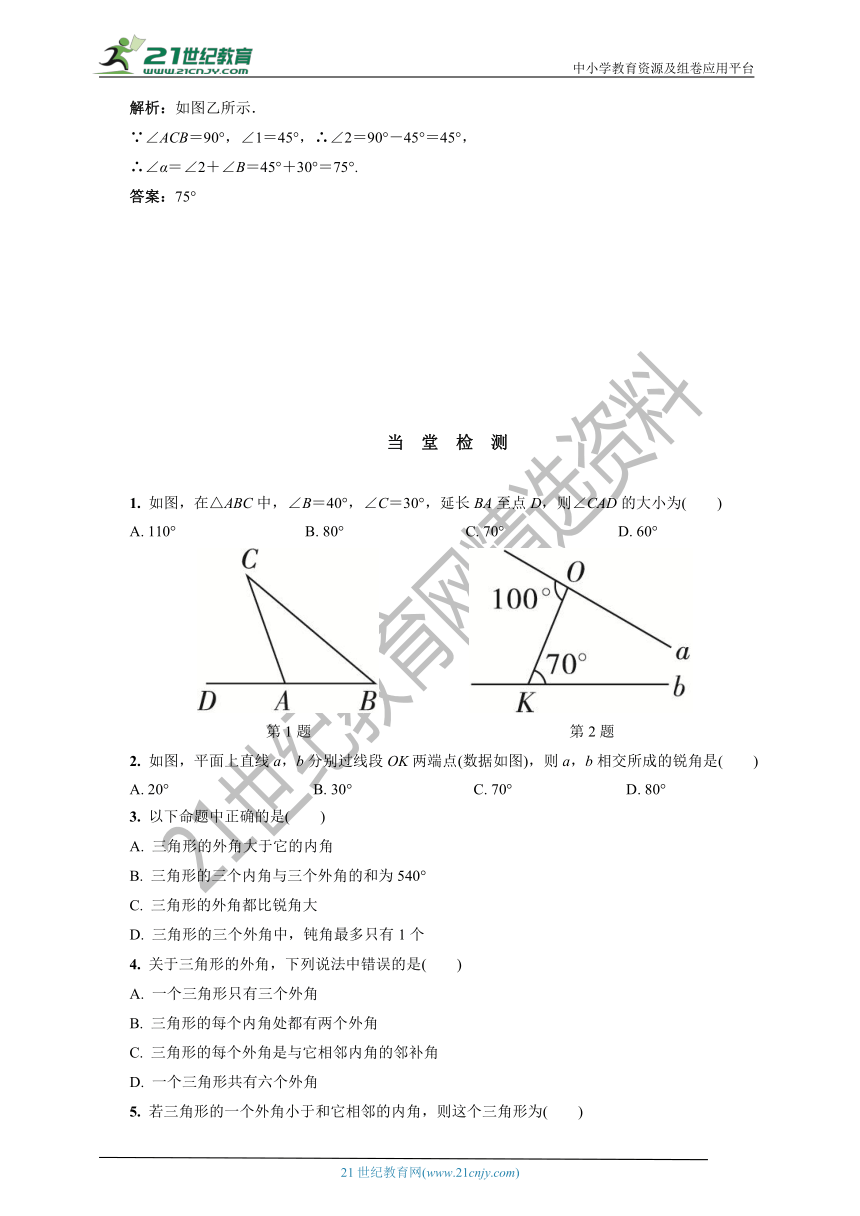
1. 如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )
A. 110° B. 80° C. 70° D. 60°
第1题 第2题
2. 如图,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角是( )
A. 20° B. 30° C. 70° D. 80°
3. 以下命题中正确的是( )
A. 三角形的外角大于它的内角
B. 三角形的三个内角与三个外角的和为540°
C. 三角形的外角都比锐角大
D. 三角形的三个外角中,钝角最多只有1个
4. 关于三角形的外角,下列说法中错误的是( )
A. 一个三角形只有三个外角
B. 三角形的每个内角处都有两个外角
C. 三角形的每个外角是与它相邻内角的邻补角
D. 一个三角形共有六个外角
5. 若三角形的一个外角小于和它相邻的内角,则这个三角形为( )
A. 锐角三角形 B. 直线三角形
C. 钝角三角形 D. 无法确定
6. 如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A. 85° B. 80° C. 75° D. 70°
第6题 第7题
7. 如图,△CEF的外角为 .
8. 如图,已知∠1=100°,∠2=140°,那么∠3= .
第8题 第9题
9. 如图,在△ABC中,∠C=104°,BF平分∠ABC与△ABC的外角平分线AE所在的直线交于点F,则∠F= .
10. 求出图中的x的值.
11. 如图,已知∠B=10°,∠C=20°,∠BOC=110°,求∠A.(提示:延长BO交AC于点D)
当堂检测参考答案
1. C 2. B 3. B 4. A 5. C 6. A
7. ∠AFC,∠BEF
8. 60°
9. 52°
10. 解:由图知x+80=x+x+20,解得x=60.
11. 解:延长BO交AC于点D.∵∠BOC=∠ODC+∠C,∴∠ODC=∠BOC-∠C=110°-20°=90°.又∵∠ODC=∠A+∠B,∴∠A=∠ODC-∠B=90°-10°=80°.
第13章 三角形中的边角关系、命题与证明
13.2 命题与证明
13.2.4 三角形的外角
要 点 讲 解
要点一 三角形的外角的定义
1. 如图甲所示,把△ABC的一边BC延长至点D,得到∠ACD.像∠ACD这样,由三角形的一边与另一边的延长线组成的角,叫做三角形的外角.对于∠ACD而言,∠ACB是与它相邻的内角,∠A,∠B是与它不相邻的内角.
甲 乙
2. 三角形每个顶点处都有两个外角(这两个外角是对顶角,相等),通常说三角形的外角是指三角形某一顶点处的一个外角,涉及具体问题时,应该准确说明是哪个内角的一个外角.如图乙中,顶点A处的∠1,∠2是外角,但∠3不是外角.一个三角形共有6个外角.
要点二 三角形外角的性质(推论3、4)
推论3:三角形的外角等于与它不相邻的两个内角的和.
推论4:三角形的外角大于与它不相邻的任何一个内角.
在使用外角的性质时,不能忽视“不相邻”这个限制条件.
经典例题 如图甲所示是一副三角板叠放的示意图,则∠α=________.
甲 乙
解析:如图乙所示.
∵∠ACB=90°,∠1=45°,∴∠2=90°-45°=45°,
∴∠α=∠2+∠B=45°+30°=75°.
答案:75°
当 堂 检 测
1. 如图,在△ABC中,∠B=40°,∠C=30°,延长BA至点D,则∠CAD的大小为( )
A. 110° B. 80° C. 70° D. 60°
第1题 第2题
2. 如图,平面上直线a,b分别过线段OK两端点(数据如图),则a,b相交所成的锐角是( )
A. 20° B. 30° C. 70° D. 80°
3. 以下命题中正确的是( )
A. 三角形的外角大于它的内角
B. 三角形的三个内角与三个外角的和为540°
C. 三角形的外角都比锐角大
D. 三角形的三个外角中,钝角最多只有1个
4. 关于三角形的外角,下列说法中错误的是( )
A. 一个三角形只有三个外角
B. 三角形的每个内角处都有两个外角
C. 三角形的每个外角是与它相邻内角的邻补角
D. 一个三角形共有六个外角
5. 若三角形的一个外角小于和它相邻的内角,则这个三角形为( )
A. 锐角三角形 B. 直线三角形
C. 钝角三角形 D. 无法确定
6. 如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是( )
A. 85° B. 80° C. 75° D. 70°
第6题 第7题
7. 如图,△CEF的外角为 .
8. 如图,已知∠1=100°,∠2=140°,那么∠3= .
第8题 第9题
9. 如图,在△ABC中,∠C=104°,BF平分∠ABC与△ABC的外角平分线AE所在的直线交于点F,则∠F= .
10. 求出图中的x的值.
11. 如图,已知∠B=10°,∠C=20°,∠BOC=110°,求∠A.(提示:延长BO交AC于点D)
当堂检测参考答案
1. C 2. B 3. B 4. A 5. C 6. A
7. ∠AFC,∠BEF
8. 60°
9. 52°
10. 解:由图知x+80=x+x+20,解得x=60.
11. 解:延长BO交AC于点D.∵∠BOC=∠ODC+∠C,∴∠ODC=∠BOC-∠C=110°-20°=90°.又∵∠ODC=∠A+∠B,∴∠A=∠ODC-∠B=90°-10°=80°.
