1.1.1 正弦定理 课件
图片预览







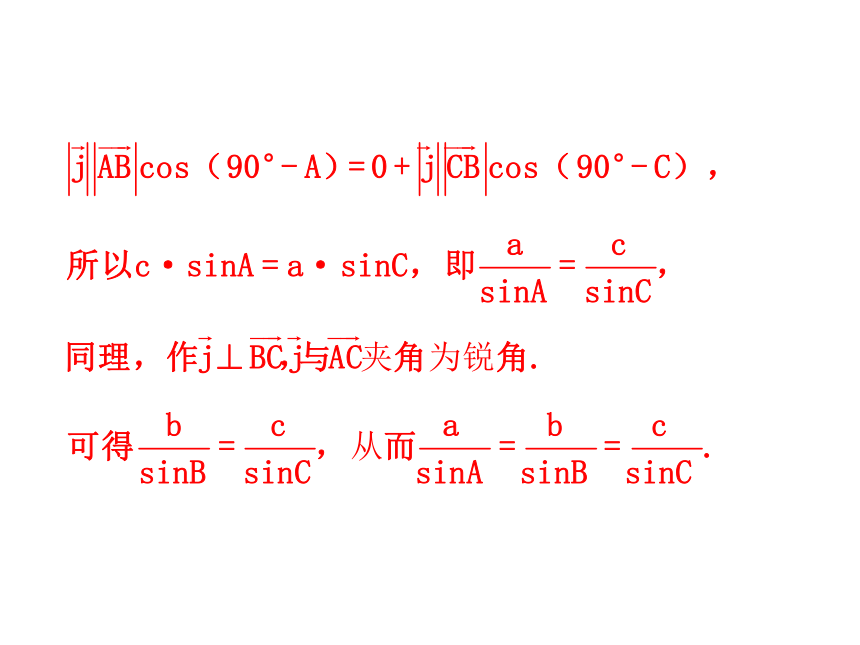
文档简介
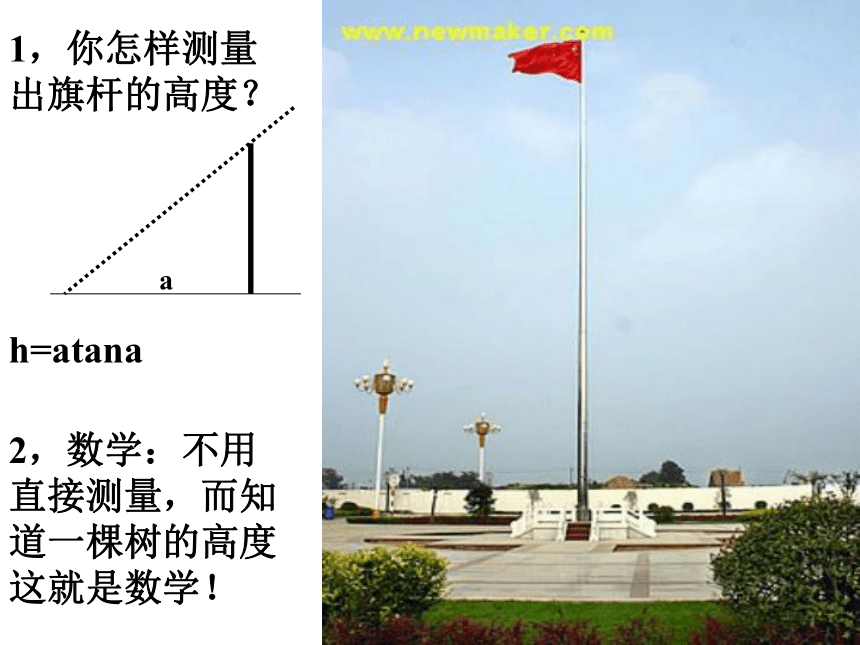
课件30张PPT。1.1.1 正弦定理第一章 解三角形自己把自己说服了,是一种理智的胜利;自己被自己感动了,是一种心灵的升华;自己把自己征服了,是一种人生的成功。1,你怎样测量出旗杆的高度?2,数学:不用直接测量,而知道一棵树的高度这就是数学!h=atanaa1.必须会用3种方法证明:正弦定理
2.熟练掌握:正弦定理的变形
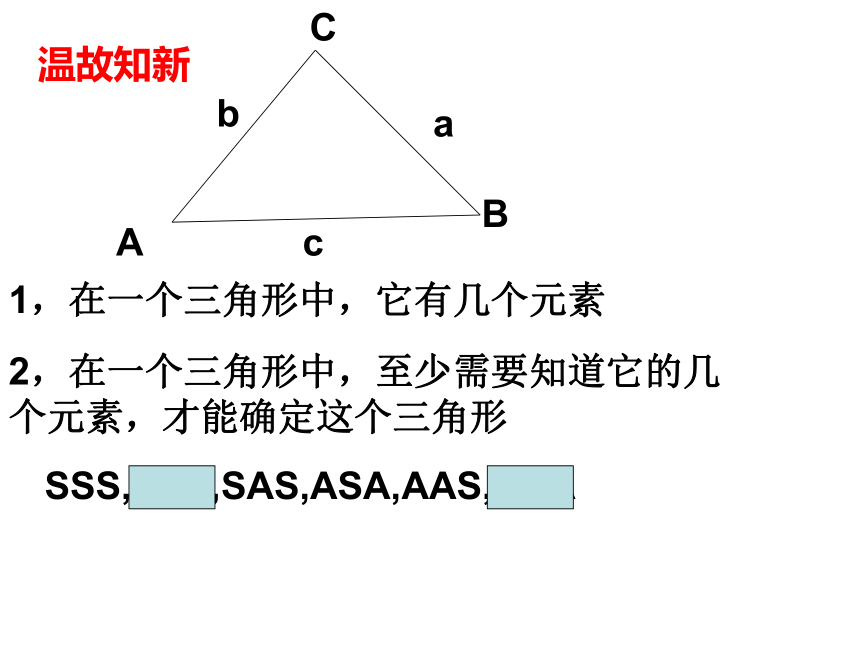
3.会用正弦定理解决问题1,在一个三角形中,它有几个元素2,在一个三角形中,至少需要知道它的几个元素,才能确定这个三角形ACBcabSSS,SSA,SAS,ASA,AAS,AAA温故知新问题一:什么叫解三角形? 一般的,三角形中的三个角A、B、C和它对应的三条边a、b、c叫做三角形的元素。
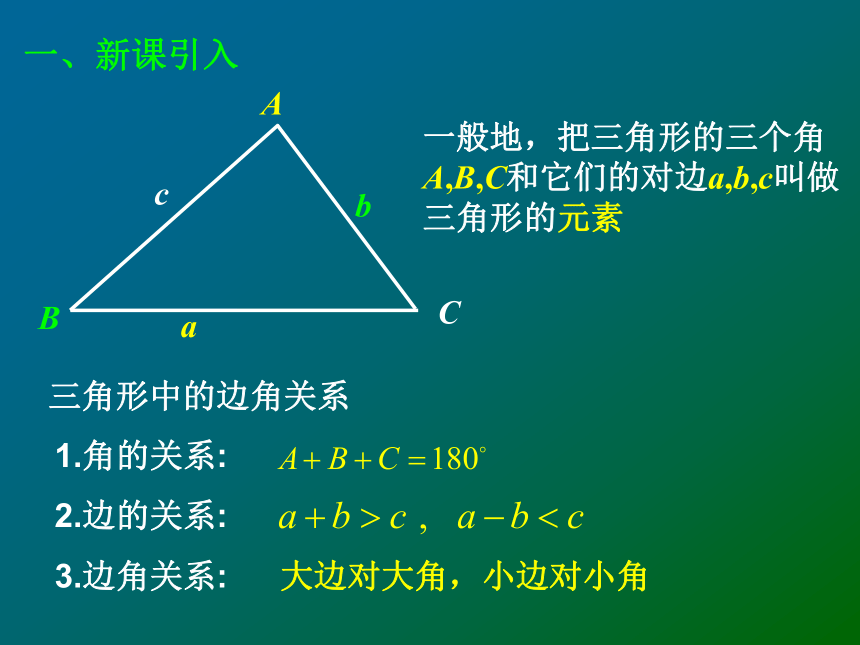
已知三角形的几( )个元素求其他元素的过程就叫解三角形3一、新课引入ABCbc三角形中的边角关系1.角的关系:
2.边的关系:
3.边角关系:大边对大角,小边对小角a一般地,把三角形的三个角
A,B,C和它们的对边a,b,c叫做
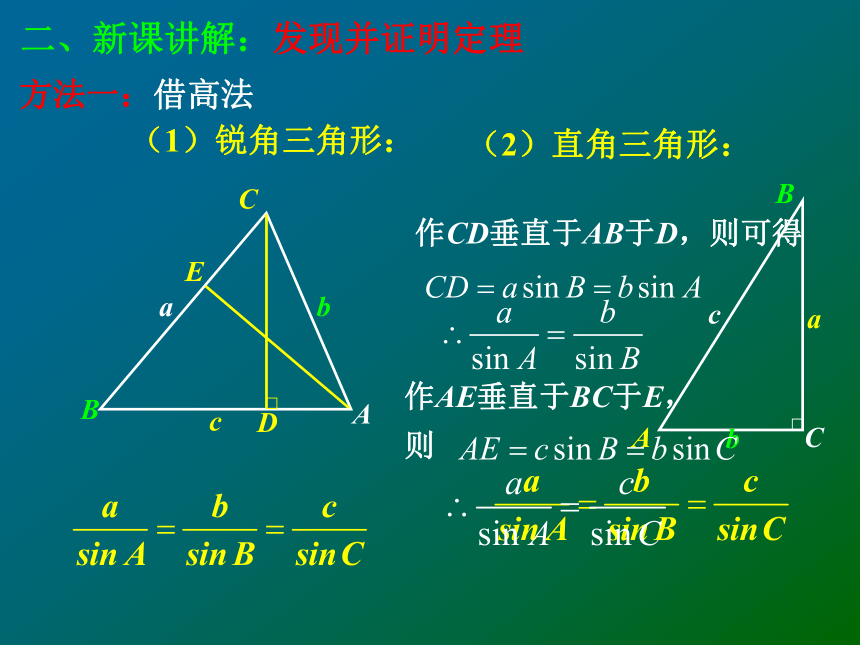
三角形的元素 小强师傅的一个三角形的模型坏了,只剩下如下图所示的部分,测量出∠A=47°, ∠C=80°, AC长为1m,如何解这个三角形?ABabcC一、新课引入方法一:借高法(1)锐角三角形:(2)直角三角形:二、新课讲解:发现并证明定理作CD垂直于AB于D,则可得作AE垂直于BC于E,
则试借助三角形的高来寻找三角形的边与角之间的关系?二、新课讲解 发现并证明定理(3)钝角三角形:(∠C为钝角)CABabc作CD垂直于AB于D,则可得作BE垂直于AC的延长线于E,则正弦定理:即在一个三角形中,各边和它所对角的
正弦的比相等.思考:你能否找到其他证明正弦定理的方法?证法二:向量法因为涉及边长问题,从而可以考虑用向量来研究此问题.CabAB证法三:外接圆法作外接圆O,过B作直径BC/,连AC/,一、正弦定理: 在一个三角形中,各边和它所对角的正弦的比相等,
即剖析定理、加深理解二、正弦定理的适用范围三、 正弦定理的变形:四、定理应用:三角形的面积公式证明:∵
而∴同理∴ha正弦定理可处理两类问题三、例题讲解例1 在△ABC中,A=32.0o,B=81.5o,a=42.9,解此三
角形.解:根据三角形的内角和定理:C=180o-(A+B)=66.2o由正弦定理可得由正弦定理可得应用正弦定理解三角形
题型一:已知两角和任意一边,求出其他两边和一角解:由正弦定理所以B=60°,或B=120°C=90°C=30°当B=120°时题型二:已知两边和其中一边的对角,求出三角形的另一边和另外两个角.三、例题讲解解:由正弦定理可得C=180o-(A+B)≈76o(1)C=180o-(A+B)≈24o(2)当B≈116o时,题型二:已知两边和其中一边的对角,求出三角形的另一边和另外两个角.例2.在△ABC中,a=20cm,b=28cm, A=40o,解此三角形.三、例题讲解解:由正弦定理可得由b<a,A=45o,可知B<A
∴C=180o-(A+B)≈107o题型二:已知两边和其中一边的对角,求出三角形的另一边和另外两个角.例2.在△ABC中,a=20cm,b=28cm, A=40o,解此三角形.若已知a、b、A的值,则解该三角形的步骤如下:
(1)先利用 求出sinB,从而求出角B;
(2)利用A、B求出角C=180o-(A+B);
(3)再利用 求出边c.三、例题讲解题型二:已知两边和其中一边的对角,求出三角形的另一边和另外两个角.注意:求角B时应注意检验!例3 在△ABC中,A=45o, ,这样的三角形有__个三、例题讲解1.画∠PAQ=45o2. 在AP上取AC=b=43.以C为圆心,a=6为半径画弧,弧与AQ的交点为BB2个1个0个1个0个1已知a、b和∠A时,解斜三角形的各种情况a≥b 一解bsinA两解bsinA=a
一解bsinA>a
无解(一)当A为锐角(二)当A为钝角a>b
一解a≤b
无解三、例题讲解(三)当A为直角若已知三角形的两条边及其中一边的对角(若已知a、b、A的值),则可用正弦定理求解,且解的情况如下A为钝角或直角A为锐角a>ba≤ba<bsinAa=bsinAbsinA<a<b一解无解无解一解两解a≥b一解2.在△ABC中,由已知条件解三角形,下列有两解的是( )
A.b=20, A=45o, C=80o B.a=30, c=28, B=60o
C.a=14, b=16, A=45o D.a=12, c=15, A=120o四、练习※判断已知两边及其中一边对角的三角形解的个数
的基本步骤(适合填空或选择题):
(1)判断已知角A的类型;(钝、直、锐)
(2)判断已知两边a、b的大小关系;
(3)判断a与bsinA的大小关系.C1.在△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,
则下列关系一定成立的是 ( )
A.a>bsinA B.a=bsinA C.a题型一:已知两角和任意一边,求出其他两边和一角注:若已知边不是对边,先用三角形内角和定理求第三角,再用正弦定理求另两边.题型二: 已知两边和其中一边的对角,求出三角形的另一边和另外两个角.注意有两解、一解、无解三种情况(求角B时应检验!)其中,R是△ABC的外接圆的半径3.利用图形判断:已知两边和其中一边的对角时解斜三角形的各种情况(注意已知角的分类)自己把自己说服了,是一种理智的胜利;自己被自己感动了,是一种心灵的升华;自己把自己征服了,是一种人生的成功。
2.熟练掌握:正弦定理的变形
3.会用正弦定理解决问题1,在一个三角形中,它有几个元素2,在一个三角形中,至少需要知道它的几个元素,才能确定这个三角形ACBcabSSS,SSA,SAS,ASA,AAS,AAA温故知新问题一:什么叫解三角形? 一般的,三角形中的三个角A、B、C和它对应的三条边a、b、c叫做三角形的元素。
已知三角形的几( )个元素求其他元素的过程就叫解三角形3一、新课引入ABCbc三角形中的边角关系1.角的关系:
2.边的关系:
3.边角关系:大边对大角,小边对小角a一般地,把三角形的三个角
A,B,C和它们的对边a,b,c叫做
三角形的元素 小强师傅的一个三角形的模型坏了,只剩下如下图所示的部分,测量出∠A=47°, ∠C=80°, AC长为1m,如何解这个三角形?ABabcC一、新课引入方法一:借高法(1)锐角三角形:(2)直角三角形:二、新课讲解:发现并证明定理作CD垂直于AB于D,则可得作AE垂直于BC于E,
则试借助三角形的高来寻找三角形的边与角之间的关系?二、新课讲解 发现并证明定理(3)钝角三角形:(∠C为钝角)CABabc作CD垂直于AB于D,则可得作BE垂直于AC的延长线于E,则正弦定理:即在一个三角形中,各边和它所对角的
正弦的比相等.思考:你能否找到其他证明正弦定理的方法?证法二:向量法因为涉及边长问题,从而可以考虑用向量来研究此问题.CabAB证法三:外接圆法作外接圆O,过B作直径BC/,连AC/,一、正弦定理: 在一个三角形中,各边和它所对角的正弦的比相等,
即剖析定理、加深理解二、正弦定理的适用范围三、 正弦定理的变形:四、定理应用:三角形的面积公式证明:∵
而∴同理∴ha正弦定理可处理两类问题三、例题讲解例1 在△ABC中,A=32.0o,B=81.5o,a=42.9,解此三
角形.解:根据三角形的内角和定理:C=180o-(A+B)=66.2o由正弦定理可得由正弦定理可得应用正弦定理解三角形
题型一:已知两角和任意一边,求出其他两边和一角解:由正弦定理所以B=60°,或B=120°C=90°C=30°当B=120°时题型二:已知两边和其中一边的对角,求出三角形的另一边和另外两个角.三、例题讲解解:由正弦定理可得C=180o-(A+B)≈76o(1)C=180o-(A+B)≈24o(2)当B≈116o时,题型二:已知两边和其中一边的对角,求出三角形的另一边和另外两个角.例2.在△ABC中,a=20cm,b=28cm, A=40o,解此三角形.三、例题讲解解:由正弦定理可得由b<a,A=45o,可知B<A
∴C=180o-(A+B)≈107o题型二:已知两边和其中一边的对角,求出三角形的另一边和另外两个角.例2.在△ABC中,a=20cm,b=28cm, A=40o,解此三角形.若已知a、b、A的值,则解该三角形的步骤如下:
(1)先利用 求出sinB,从而求出角B;
(2)利用A、B求出角C=180o-(A+B);
(3)再利用 求出边c.三、例题讲解题型二:已知两边和其中一边的对角,求出三角形的另一边和另外两个角.注意:求角B时应注意检验!例3 在△ABC中,A=45o, ,这样的三角形有__个三、例题讲解1.画∠PAQ=45o2. 在AP上取AC=b=43.以C为圆心,a=6为半径画弧,弧与AQ的交点为BB2个1个0个1个0个1已知a、b和∠A时,解斜三角形的各种情况a≥b 一解bsinA
一解bsinA>a
无解(一)当A为锐角(二)当A为钝角a>b
一解a≤b
无解三、例题讲解(三)当A为直角若已知三角形的两条边及其中一边的对角(若已知a、b、A的值),则可用正弦定理求解,且解的情况如下A为钝角或直角A为锐角a>ba≤ba<bsinAa=bsinAbsinA<a<b一解无解无解一解两解a≥b一解2.在△ABC中,由已知条件解三角形,下列有两解的是( )
A.b=20, A=45o, C=80o B.a=30, c=28, B=60o
C.a=14, b=16, A=45o D.a=12, c=15, A=120o四、练习※判断已知两边及其中一边对角的三角形解的个数
的基本步骤(适合填空或选择题):
(1)判断已知角A的类型;(钝、直、锐)
(2)判断已知两边a、b的大小关系;
(3)判断a与bsinA的大小关系.C1.在△ABC中,∠A,∠B,∠C所对的边分别是a,b,c,
则下列关系一定成立的是 ( )
A.a>bsinA B.a=bsinA C.a
