1.1.2 余弦定理 课件
图片预览











文档简介
课件38张PPT。1.1.2 余弦定理第一章 解三角形自安于弱,而终于弱矣;自安于遇,而终于愚矣。 ——吕祖谦(1)正弦定理可以解决三角形中的问题:① 已知两角和一边,求其他角和边 ②已知两边和其中一边的对角,求另一边
的对角,进而可求其他的边和角1.复习回顾:(3) 正弦定理的变形:(2) 三角形面积公式: 如果已知一个三角形的两条边及其夹角,根据三角形全等的定理,该三角形大小形状完全确定,那么如何解出这个三角形呢?思考:1.掌握余弦定理的两种表示形式及证明余弦定理的三种方法.(重点)2.会运用余弦定理解决两类基本的解三角形问题.(难点)思考: 在△ABC中,已知CB=a,CA=b,CB
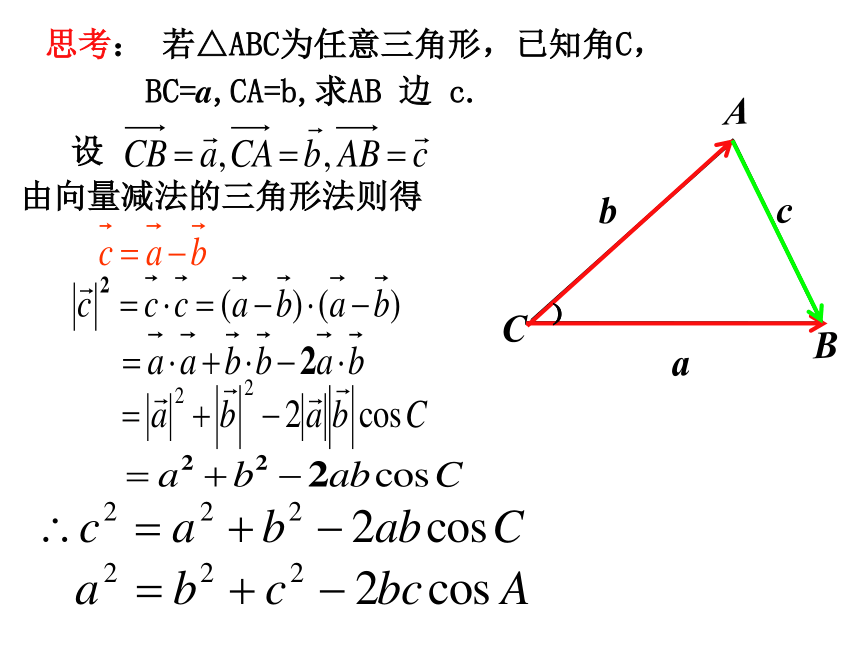
与CA的夹角为∠C, 求边c.﹚由向量减法的三角形法则得2.余弦定理法一:向量法CBAcab﹚﹚由向量减法的三角形法则得思考: 若△ABC为任意三角形,已知角C,
BC=a,CA=b,求AB 边 c.CBAcab﹚余弦定理由向量减法的三角形法则得思考: 若△ABC为任意三角形,已知角C,
BC=a,CA=b,求AB 边 c.余 弦 定 理 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:法二:解析法当角C为锐角时法三:几何法当角C为钝角时 余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。证明:在三角形ABC中,已知AB=c,AC=b, 作CD⊥AB,则CD=bsinA,BD=c-bcosA推论:(1)已知两边和它们的夹角,求第三边和其
他两个角;3.余弦定理的应用例3 在△ABC中,已知b=3cm,c=4cm,A=600 ,解三角形。练习2. 已知△ABC中,a=8,b=7,B=600,
求c及S△ABC整理得:c2-8c+15=0解得:c1=3, c2=5(2)已知三边,求三个角。例4.在△ABC中,已知a= ,b=2,
c= ,解三角形.例4.在△ABC中,已知a= ,b=2,
c= ,解三角形.解:由余弦定理得(3)判断三角形的形状例5 在△ABC中, ,
那么A是( )A. 钝角 B. 直角
C. 锐角 D. 不能确定A提炼:设a是最长的边,则6. 在△ABC中,已知a=7,b=10,c=6,
判定△ABC的形状分析: △ABC的形状是由大边b所对的大角
B决定的。变式:若已知三边的比是7:10:6,怎么求解 练习:7.一钝角三角形的边长为连续自然数,则这三边长为( ) 分析: 要看哪一组符合要求,只需检验哪一个选项中的最大角是钝角,即该角的余弦值小于0。BA. 1,2,3 B. 2,3,4
C. 3,4,5 D. 4,5,68.在△ABC中,已知a=7,b=8,cosC= , 求最大角的余弦值分析:求最大角的余弦值,最主要的是判断哪个角是最大角。由大边对大角,已知两边可求出第三边,找到最大角。则有:b是最大边,那么B 是最大角由A+B+C=180°求角A,由正弦定理
求出b与c.解三角形的四种基本类型正弦定理余弦定理由余弦定理求出第三边c,再由正弦定理求出剩下的角.正弦定理由正弦定理求出角B,再求角C,最后求出c边.可有两解,一解或无解.余弦定理先由余弦定理求出其中两个角,再利用内角和为180°求出第三个角.4.小结:(1)余弦定理:(2)推论: (3)余弦定理可以解决的有关三角形的问题:
已知两边及其夹角,求第三边和其他
两个角。
2) 已知三边求三个角。
3) 判断三角形的形状。例1.如图所示,有两条直线AB和CD 相交成80 °角,交点是O,甲、乙两人同时从点O分别沿OA,OC方向出发,速度分别是4km/h,4.5km/h。3时后两人相距多远(精确到0.1km)?ODAQCBP80°解 经过3时后,甲到达点P,OP=4×3=12(km),乙到达点Q,OQ=4.5×3=13.5(km)。依余弦定理,知数学应用:例2.在长江某渡口处,江水以5km/h的速度
向东流。一渡船在江南岸的A码头出发,预定
要在0.1h后到达江北岸B码头,设AN为正北
方向,已知B码头在A码头的北偏东15°,
并与A码头相距1.2km.该渡船应按什么方向
航行?速度是多少千米/小时?数学应用:数学应用:在ΔABC中,由余弦定理,得所以AD=BC≈1.17(km)因此,船的航行速度为
1.17÷0.1=11.7(km/h)在△ABC中,由正弦定理,得所以 ∠ABC≈24.4°所以∠DAN=∠DAB-∠NAB=
∠ABC-15 ° ≈9.4 °答:渡船按北偏西9.4 °的
方向,并以11.7km/h的
速度航行.数学应用:思考:想想看有无其它的方法?数学应用:变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。解:由正弦定理,
R为△ABC的外接圆半径,将原式化为4R2sin2Bsin2C+4R2sin2Csin2B
=8R2sinBsinCcosBcosC, 所以8R2sin2Bsin2C=8R2sinBsinCcosBcosC, 因为sinBsinC≠0,所以sinBsinC=cosBcosC,
即cos(B+C)=0, 从而∠B+∠C=90°,∠A=90°,
故△ABC为直角三角形。 变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。自安于弱,而终于弱矣;自安于遇,而终于愚矣。 ——吕祖谦
的对角,进而可求其他的边和角1.复习回顾:(3) 正弦定理的变形:(2) 三角形面积公式: 如果已知一个三角形的两条边及其夹角,根据三角形全等的定理,该三角形大小形状完全确定,那么如何解出这个三角形呢?思考:1.掌握余弦定理的两种表示形式及证明余弦定理的三种方法.(重点)2.会运用余弦定理解决两类基本的解三角形问题.(难点)思考: 在△ABC中,已知CB=a,CA=b,CB
与CA的夹角为∠C, 求边c.﹚由向量减法的三角形法则得2.余弦定理法一:向量法CBAcab﹚﹚由向量减法的三角形法则得思考: 若△ABC为任意三角形,已知角C,
BC=a,CA=b,求AB 边 c.CBAcab﹚余弦定理由向量减法的三角形法则得思考: 若△ABC为任意三角形,已知角C,
BC=a,CA=b,求AB 边 c.余 弦 定 理 三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。证明:以CB所在的直线为x轴,过C点垂直于CB的直线为y轴,建立如图所示的坐标系,则A、B、C三点的坐标分别为:法二:解析法当角C为锐角时法三:几何法当角C为钝角时 余弦定理作为勾股定理的推广,考虑借助勾股定理来证明余弦定理。证明:在三角形ABC中,已知AB=c,AC=b, 作CD⊥AB,则CD=bsinA,BD=c-bcosA推论:(1)已知两边和它们的夹角,求第三边和其
他两个角;3.余弦定理的应用例3 在△ABC中,已知b=3cm,c=4cm,A=600 ,解三角形。练习2. 已知△ABC中,a=8,b=7,B=600,
求c及S△ABC整理得:c2-8c+15=0解得:c1=3, c2=5(2)已知三边,求三个角。例4.在△ABC中,已知a= ,b=2,
c= ,解三角形.例4.在△ABC中,已知a= ,b=2,
c= ,解三角形.解:由余弦定理得(3)判断三角形的形状例5 在△ABC中, ,
那么A是( )A. 钝角 B. 直角
C. 锐角 D. 不能确定A提炼:设a是最长的边,则6. 在△ABC中,已知a=7,b=10,c=6,
判定△ABC的形状分析: △ABC的形状是由大边b所对的大角
B决定的。变式:若已知三边的比是7:10:6,怎么求解 练习:7.一钝角三角形的边长为连续自然数,则这三边长为( ) 分析: 要看哪一组符合要求,只需检验哪一个选项中的最大角是钝角,即该角的余弦值小于0。BA. 1,2,3 B. 2,3,4
C. 3,4,5 D. 4,5,68.在△ABC中,已知a=7,b=8,cosC= , 求最大角的余弦值分析:求最大角的余弦值,最主要的是判断哪个角是最大角。由大边对大角,已知两边可求出第三边,找到最大角。则有:b是最大边,那么B 是最大角由A+B+C=180°求角A,由正弦定理
求出b与c.解三角形的四种基本类型正弦定理余弦定理由余弦定理求出第三边c,再由正弦定理求出剩下的角.正弦定理由正弦定理求出角B,再求角C,最后求出c边.可有两解,一解或无解.余弦定理先由余弦定理求出其中两个角,再利用内角和为180°求出第三个角.4.小结:(1)余弦定理:(2)推论: (3)余弦定理可以解决的有关三角形的问题:
已知两边及其夹角,求第三边和其他
两个角。
2) 已知三边求三个角。
3) 判断三角形的形状。例1.如图所示,有两条直线AB和CD 相交成80 °角,交点是O,甲、乙两人同时从点O分别沿OA,OC方向出发,速度分别是4km/h,4.5km/h。3时后两人相距多远(精确到0.1km)?ODAQCBP80°解 经过3时后,甲到达点P,OP=4×3=12(km),乙到达点Q,OQ=4.5×3=13.5(km)。依余弦定理,知数学应用:例2.在长江某渡口处,江水以5km/h的速度
向东流。一渡船在江南岸的A码头出发,预定
要在0.1h后到达江北岸B码头,设AN为正北
方向,已知B码头在A码头的北偏东15°,
并与A码头相距1.2km.该渡船应按什么方向
航行?速度是多少千米/小时?数学应用:数学应用:在ΔABC中,由余弦定理,得所以AD=BC≈1.17(km)因此,船的航行速度为
1.17÷0.1=11.7(km/h)在△ABC中,由正弦定理,得所以 ∠ABC≈24.4°所以∠DAN=∠DAB-∠NAB=
∠ABC-15 ° ≈9.4 °答:渡船按北偏西9.4 °的
方向,并以11.7km/h的
速度航行.数学应用:思考:想想看有无其它的方法?数学应用:变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。解:由正弦定理,
R为△ABC的外接圆半径,将原式化为4R2sin2Bsin2C+4R2sin2Csin2B
=8R2sinBsinCcosBcosC, 所以8R2sin2Bsin2C=8R2sinBsinCcosBcosC, 因为sinBsinC≠0,所以sinBsinC=cosBcosC,
即cos(B+C)=0, 从而∠B+∠C=90°,∠A=90°,
故△ABC为直角三角形。 变式训练: 在△ABC中,若b2sin2C+c2sin2B
=2bc·cosBcosC,试判断三角形的形状。自安于弱,而终于弱矣;自安于遇,而终于愚矣。 ——吕祖谦
