1.2 应用举例 课件

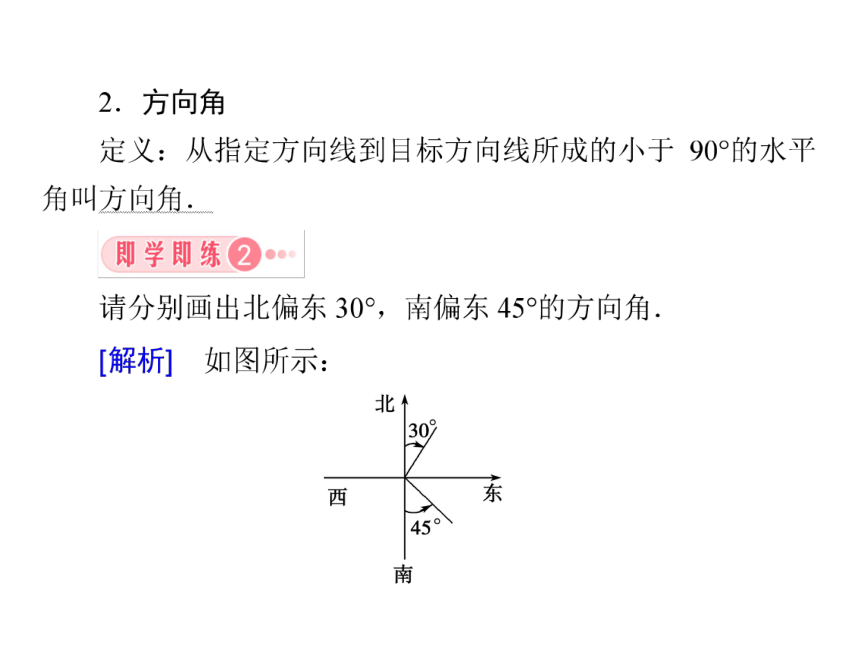
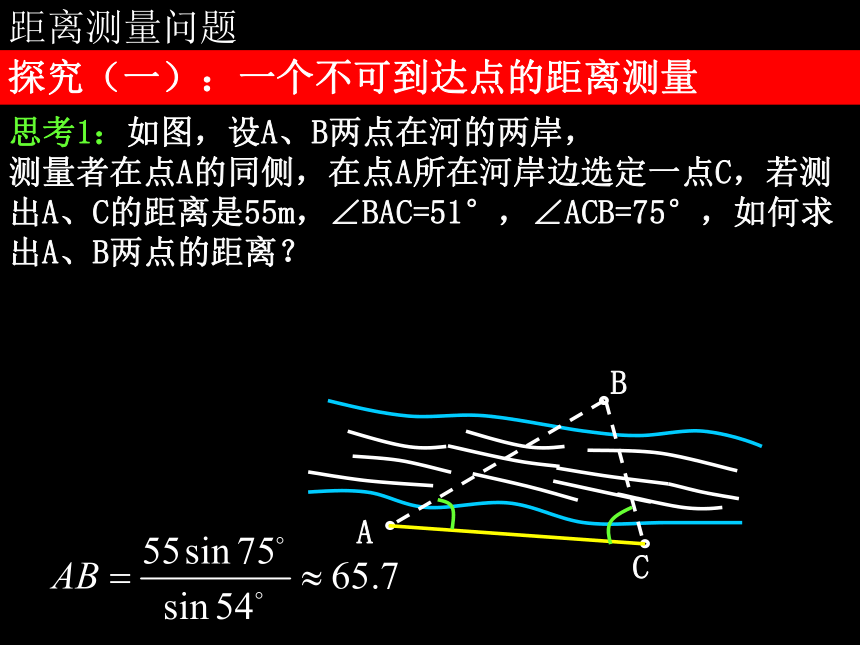
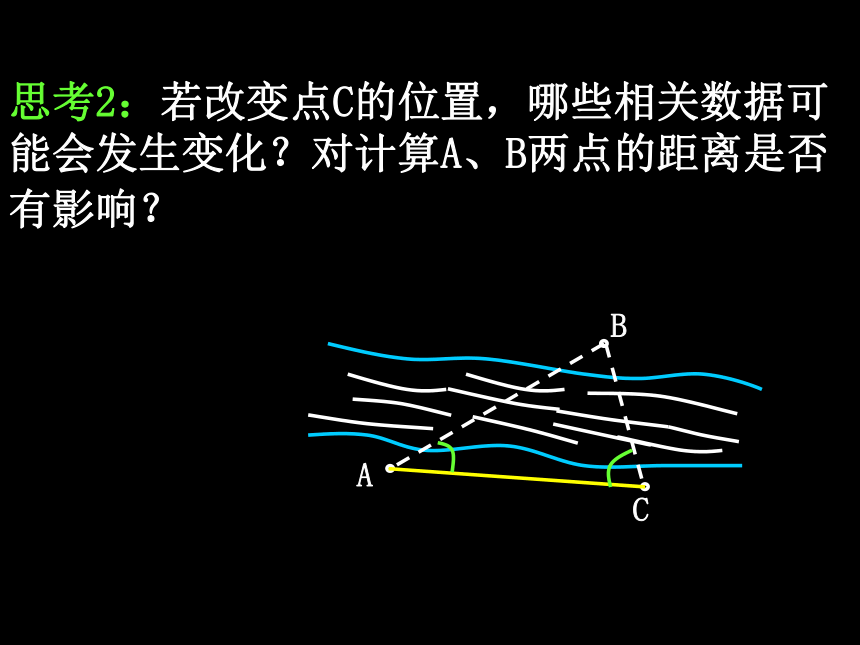
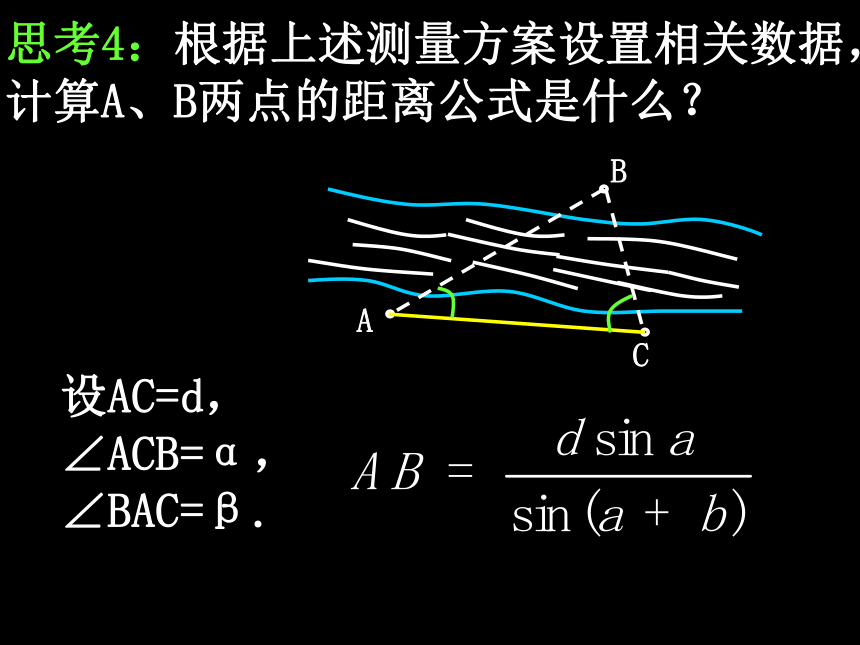
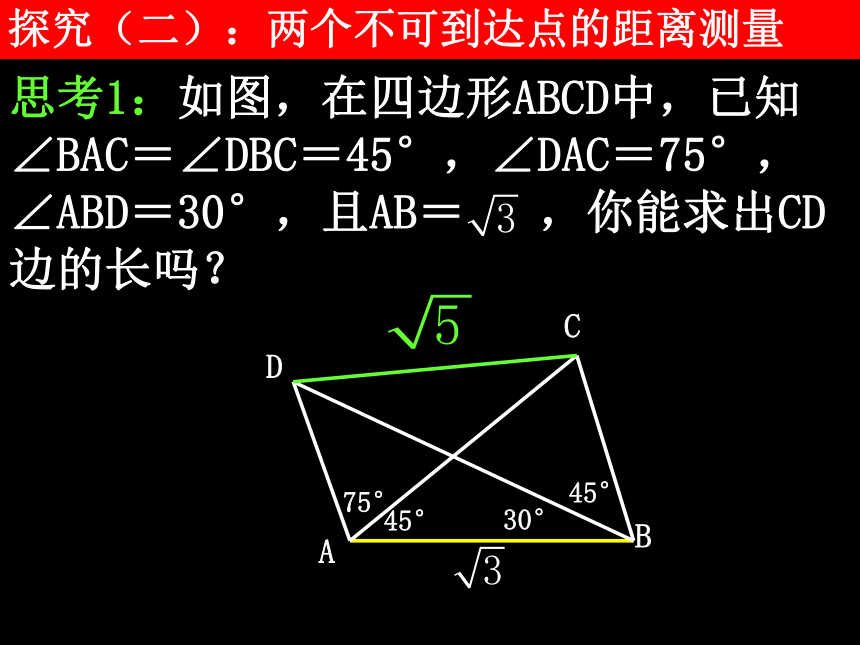
课件38张PPT。1.2 应用举例第一章 解三角形问题提出1.正弦定理和余弦定理的基本公式是什么？2.正弦定理和余弦定理分别适合解哪些类型的三角形？正弦定理：一边两角或两边与对角； 余弦定理：两边与夹角或三边.3.在平面几何中，两点间的距离就是连接这两点的线段长.对于不可以直接度量的两点间的距离，通常用什么办法进行计算？ 构造三角形4.在测量问题中，对于可到达的点之间的距离，一般直接度量，对于不可到达的两点间的距离，常在特定情境下通过解三角形进行计算，我们将对这类问题作些实例分析. 距离测量问题探究（一）：一个不可到达点的距离测量思考2：若改变点C的位置，哪些相关数据可能会发生变化？对计算A、B两点的距离是否有影响？ 思考3：一般地，若A为可到达点，B为不可到达点，应如何设计测量方案计算A、B两点的距离？选定一个可到达点C； →测量AC的距离及∠BAC，∠ACB的大小 →利用正弦定理求AB的距离.思考4：根据上述测量方案设置相关数据，计算A、B两点的距离公式是什么？ 设AC=d，∠ACB=α，∠BAC=β. 探究（二）：两个不可到达点的距离测量思考2：设A、B两点都在河的对岸（不可到达），你能设计一个测量方案计算A、B两点间的距离吗？选定两个可到达点C、D； →测量C、D间的距离及∠ACB、∠ACD、∠BDC、∠ADB的大小；→利用正弦定理求AC和BC； →利用余弦定理求AB.思考3：在上述测量方案中，设CD=a，∠ACB=α，∠ACD=β，∠BDC=γ，∠ADB=δ，那么AC和BC的计算公式是什么？ 思考4：测量两个不可到达点之间的距离还有别的测量方法吗？理论迁移 例 某观测站C在城A的南偏西20°方向，由城A出发的一条公路沿南偏东40°方向笔直延伸.在C处测得公路上B处有一人与观测站C相距31km，此人沿公路走了20km后到达D处，测得C、D间的距离是21km；问这个人还要走多远才能到达A城？ 15问题提出1.测量一个可到达点与一个不可到达点之间的距离，应如何测量和计算？2.测量两个不可到达点之间的距离，应如何测量和计算？3.竖直方向两点间的距离，通常称为高度.如何测量顶部或底部不可到达的物体的高度，也是一个值得探究的问题.探究（一）：利用仰角测量高度计算AC的长高度测量问题思考2：取水平基线CD，只要测量出哪些数据就可计算出AC的长？点C、D观察A的仰角和CD的长 思考3：设在点C、D出测得A的仰角分别为α、β，CD=a，测角仪器的高度为h，那么建筑物高度AB的计算公式是什么？思考4：如图，在山顶上有一座铁塔BC，塔顶和塔底都可到达，A为地面上一点，通过测量哪些数据，可以计算出山顶的高度？思考5：设在点A处测得点B、C的仰角分别为α、β，铁塔的高BC=a，测角仪的高度忽略不计，那么山顶高度CD的计算公式是什么？ 探究（二）：利用俯角测量高度思考1：飞机的海拔飞行高度是可知的，若飞机的航线和山顶在同一个铅垂平面内，飞机在水平飞行中测量山顶的高度，关键是求出哪个数据？飞机与山顶的海拔差 思考2：如图，设飞机在飞临山顶前，在B、C两处测得山顶A的俯角分别是α、β，B、C两点的飞行距离为a，飞机的海拔飞行高度是H，那么山顶的海拔高度h的计算公式是什么？探究（三）：借助方位角测量高度1047m思考2：若在A、B两处测得山顶D的仰角分别为α、β，从A到B的行驶距离为a，能否求出此山的高度？思考3：在上述条件下，若在A处还测得山顶D的方向角是西偏北θ方向，能否求出此山的高度？问题提出1.测量水平面内两点间的距离，有哪两种类型？分别测量哪些数据？一个可到达点与一个不可到达点之间的距离；两个不可到达点之间的距离. 基线长和张角.2.测量物体的高度时，对角的测量有哪几种类型？在实际问题中如何选择？仰角、俯角或方位角. 在地面测仰角， 在空中测俯角， 在行进中测方位角. 3.角度是三角形的基本元素，是反映实际问题中物体方向的几何量，根据相关数据计算角的大小，也是测量问题中的一个重要内容.探究（一）：测量行进方向思考1：一艘海轮从海港A出发，沿北偏东75°的方向航行67.5 n mile后到达海岛B，然后从B出发，沿北偏东32°的方向航行54.0 n mile后到达海岛C，那么A、C 两点间的直线距离是否确定？如何计算？AC=113.15海里角度测量问题思考2：在上述问题中，AC在北偏东多少度的方向上？沿北偏东56°的方向航行 思考3：甲船在A处发现乙船在北偏东60°的B处，以20 n mile/h的速度向正北方向航行，若使甲船在直线航行中，与乙船在某处相遇，那么甲船的航行方向由什么因素所确定？ 甲船的航行速度思考4：在上述问题中，若甲船的航速为 n mile/h，那么甲船应沿什么方向航行才能与乙船在C处相遇？ 沿北偏东30°的方向航行 探究（二）：测量相对位置思考1：甲船在A处，乙船在点A的东偏南45°方向，且与甲船相距9 n mile的B处.在点B南偏西15°方向有一个小岛C，甲、乙两船分别以28 n mile/h和20 n mile/h的速度同时向小岛直线航行，并同时达到小岛，那么B处与小岛的距离是多少？15 海里思考2：在A处观察小岛，其位置如何？南偏东7°，相距21海里理论迁移 例 在A处有一条小船，在点A的北偏东30°方向有一个小岛B，这附近海域内有北偏东60°方向，且速度为4 nmile/h的潮流.已知小船的航速是10 nmile/h，若使小船在最短的时间内达到小岛，小船应沿什么方向航行？ 北偏东 18.46° 总结1.利用正弦定理和余弦定理解三角形求角的大小，是角度测量问题的基本内容，主要应用于航海中航行方向的测量与计算.2.角与距离是密切相关的，将背景材料中的相关数据转化为三角形的边角值，再利用正、余弦定理求相关角的大小，是解题的基本思路.3.如果角或距离不能直接利用正、余弦定理求解，就用方程思想处理.装饰对于德行也同样是格格不入的，因为德行是灵魂的力量和生气。
——卢梭