第一章 解三角形 归纳整合(18页)课件
文档属性
| 名称 | 第一章 解三角形 归纳整合(18页)课件 | 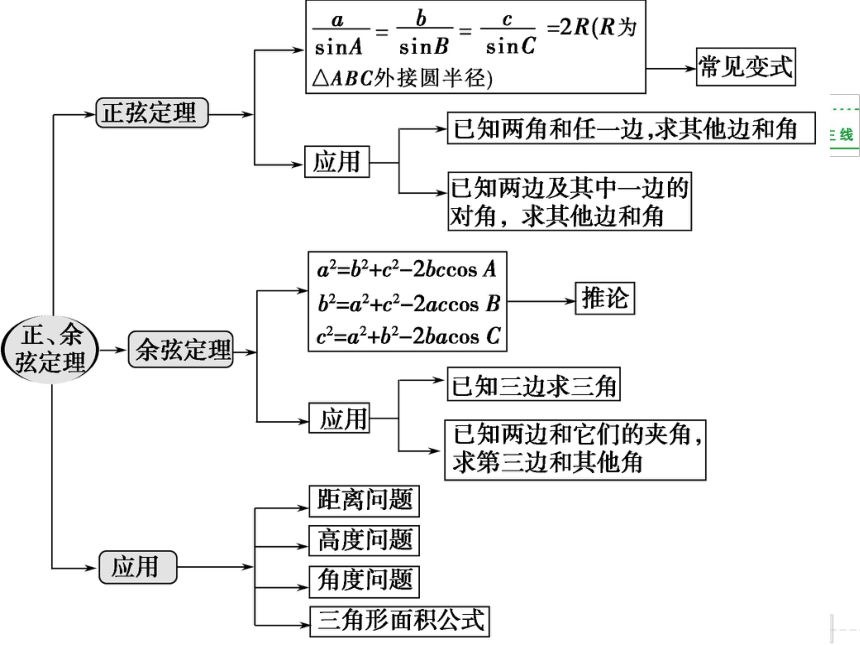 | |
| 格式 | zip | ||
| 文件大小 | 375.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-01 16:33:49 | ||
图片预览






文档简介
课件18张PPT。知识网络本章归纳整合解三角形常见类型及解法
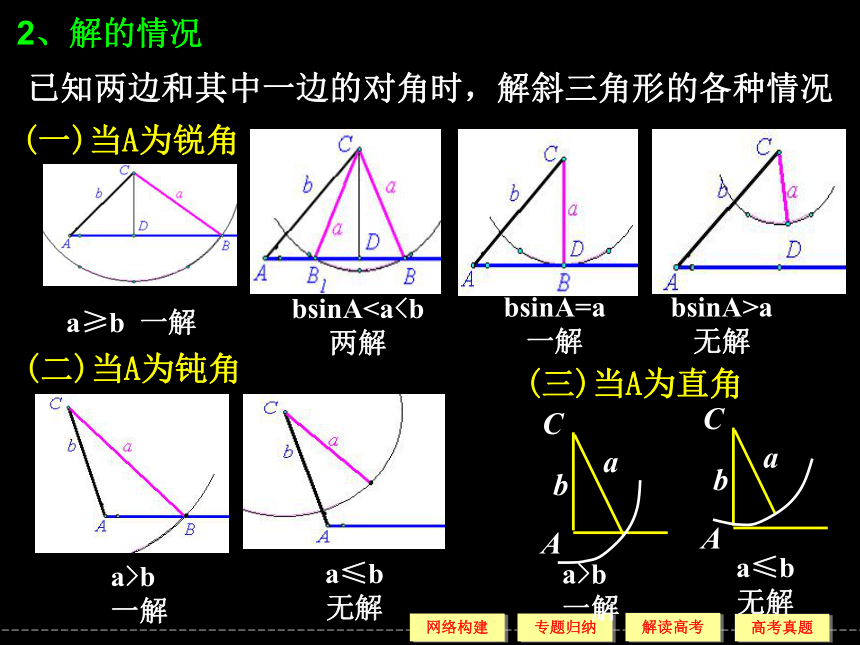
在三角形的6个元素中要知三个(除三角外)才能求解,常见类型及其解法见下表:要点归纳1.已知两边和其中一边的对角时,解斜三角形的各种情况a≥b 一解bsinA两解bsinA=a
一解bsinA>a
无解(一)当A为锐角(二)当A为钝角a>b
一解a≤b
无解2、解的情况(三)当A为直角解三角形应用题的基本思路
解三角形应用题的关键是将实际问题转化为解三角形问题来解决.其基本解题思路是:首先分析此题属于哪种类型的问题(如:测量距离、高度、角度等),然后依题意画出示意图,把已知量和未知量标在示意图中(目的是发现已知量与未知量之间的关系),最后确定用哪个定理转化,哪个定理求解,并进行作答.解题时还要注意近似计算的要求.
4.专题一 正、余弦定理的基本应用
应用正、余弦定理解三角形问题往往和面积公式、正、余弦定理的变形等结合.在解三角形时,注意挖掘题目中的隐含条件和正、余弦定理的变形应用,注意公式的选择和方程思想的应用. 在△ABC中,角A,B,C所对的边长分别为a,b,c,【例1】 在高考中,正、余弦定理与向量、三角函数的综合命题出现的较频繁,解决与三角形有关的问题时,有时除了运用正、余弦定理外,还会用到三角形的面积公式,两角和与差的三角函数公式,倍角、半角公式、向量的计算公式等.因此,应结合题目给定条件,综合运用正弦定理、余弦定理以及相关知识解题.
专题二 正、余弦定理解三角形中的综合问题
在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a-b)cos C=c·cos B,△ABC的面积S=10 ,c=7.
(1)求角C;
(2)求a,b的值.
解 (1)∵(2a-b)cos C=ccos B,
∴(2sin A-sin B)cos C=sin Ccos B,
2sin Acos C-sin Bcos C=cos Bsin C,
即2sin Acos C=sin(B+C),
∴2sin Acos C=sin A.
【例2】解斜三角形应用题的步骤:
(1)准确理解题意,分清已知与所求,准确理解应用题中的有关名称、术语,如仰角、俯角、视角、方位角等.
(2)根据题意画出图形.
(3)将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识建立数学模型,然后正确求解,演算过程要简练,计算要准确,最后作答.
专题三 解斜三角形在实际问题中的应用
如图,a是海面上一条南北方向
的海防警戒线,在a上点A处有一个
水声监测点,另两个监测点B,C分
别在A的正东方20 km和54 km处.某
时刻,监测点B收到发自静止目标P的一个声波信号,8 s后监测点A,20 s后监测点C相继收到这一信号,在当时气象条件下,声波在水中的传播速度是1.5 km/s.
(1)设A到P的距离为x km,用x表示B,C到P的距离,并求x的值;
(2)求静止目标P到海防警戒线a的距离(精确到0.01 km).
解 (1)由题意PA-PB=1.5×8=12(km),PC-PB=1.5×20=30(km).
∴PB=(x-12)(km),PC=(18+x)(km).
【例3】 与函数思想相联系的就是方程思想.所谓方程思想,就是在解决问题时,用事先设定的未知数沟通问题所涉及的各量间的制约关系,列出方程(组),从而求出未知数及各量的值,使问题获得解决,所设的未知数沟通了变量之间的联系.方程可以看做未知量与已知量相互制约的条件,它架设了由已知探索未知的桥梁.
函数与方程思想在数学中有着广泛的应用,本章在利用正、余弦定理求角或边长时,往往渗透着函数与方程思想.
专题四 函数与方程思想
在△ABC中,已知A>B>C,且A=2C,b=4,a+c=8,求a,c的长.
【例4】 解斜三角形是高考的热点内容,经常和三角化简、向量运算等联系在一起综合考查,既可能以选择题和填空题的方式也可能以解答题的形式进行考查,解答题的难度属于中低档的问题.
具体的命题过程有如下规律:
一是考查三角形的角的问题.求三角形的角常用到的工具有三角形内角和为180°,正、余弦定理及其变式,经常与三角化简求值联系在一起考查.
二是考查三角形的面积.三角形面积的处理途径比较多,需要根据条件,恰当的进行选择,实际上最终转化为三角形的边角问题解决.
命题趋势 三是对解三角形的综合问题的考查.一般题目给出边角满足的关系式,问题处理的重点是正、余弦定理的选择.需要熟练掌握正、余弦定理和三角形面积公式以及之间的联系,灵活应用二倍角公式、两角和与差公式等进行化简;不仅会利用方程思想求值,还要会利用函数思想讨论最值问题.
在三角形的6个元素中要知三个(除三角外)才能求解,常见类型及其解法见下表:要点归纳1.已知两边和其中一边的对角时,解斜三角形的各种情况a≥b 一解bsinA
一解bsinA>a
无解(一)当A为锐角(二)当A为钝角a>b
一解a≤b
无解2、解的情况(三)当A为直角解三角形应用题的基本思路
解三角形应用题的关键是将实际问题转化为解三角形问题来解决.其基本解题思路是:首先分析此题属于哪种类型的问题(如:测量距离、高度、角度等),然后依题意画出示意图,把已知量和未知量标在示意图中(目的是发现已知量与未知量之间的关系),最后确定用哪个定理转化,哪个定理求解,并进行作答.解题时还要注意近似计算的要求.
4.专题一 正、余弦定理的基本应用
应用正、余弦定理解三角形问题往往和面积公式、正、余弦定理的变形等结合.在解三角形时,注意挖掘题目中的隐含条件和正、余弦定理的变形应用,注意公式的选择和方程思想的应用. 在△ABC中,角A,B,C所对的边长分别为a,b,c,【例1】 在高考中,正、余弦定理与向量、三角函数的综合命题出现的较频繁,解决与三角形有关的问题时,有时除了运用正、余弦定理外,还会用到三角形的面积公式,两角和与差的三角函数公式,倍角、半角公式、向量的计算公式等.因此,应结合题目给定条件,综合运用正弦定理、余弦定理以及相关知识解题.
专题二 正、余弦定理解三角形中的综合问题
在△ABC中,角A,B,C的对边分别为a,b,c,且满足(2a-b)cos C=c·cos B,△ABC的面积S=10 ,c=7.
(1)求角C;
(2)求a,b的值.
解 (1)∵(2a-b)cos C=ccos B,
∴(2sin A-sin B)cos C=sin Ccos B,
2sin Acos C-sin Bcos C=cos Bsin C,
即2sin Acos C=sin(B+C),
∴2sin Acos C=sin A.
【例2】解斜三角形应用题的步骤:
(1)准确理解题意,分清已知与所求,准确理解应用题中的有关名称、术语,如仰角、俯角、视角、方位角等.
(2)根据题意画出图形.
(3)将要求解的问题归结到一个或几个三角形中,通过合理运用正弦定理、余弦定理等有关知识建立数学模型,然后正确求解,演算过程要简练,计算要准确,最后作答.
专题三 解斜三角形在实际问题中的应用
如图,a是海面上一条南北方向
的海防警戒线,在a上点A处有一个
水声监测点,另两个监测点B,C分
别在A的正东方20 km和54 km处.某
时刻,监测点B收到发自静止目标P的一个声波信号,8 s后监测点A,20 s后监测点C相继收到这一信号,在当时气象条件下,声波在水中的传播速度是1.5 km/s.
(1)设A到P的距离为x km,用x表示B,C到P的距离,并求x的值;
(2)求静止目标P到海防警戒线a的距离(精确到0.01 km).
解 (1)由题意PA-PB=1.5×8=12(km),PC-PB=1.5×20=30(km).
∴PB=(x-12)(km),PC=(18+x)(km).
【例3】 与函数思想相联系的就是方程思想.所谓方程思想,就是在解决问题时,用事先设定的未知数沟通问题所涉及的各量间的制约关系,列出方程(组),从而求出未知数及各量的值,使问题获得解决,所设的未知数沟通了变量之间的联系.方程可以看做未知量与已知量相互制约的条件,它架设了由已知探索未知的桥梁.
函数与方程思想在数学中有着广泛的应用,本章在利用正、余弦定理求角或边长时,往往渗透着函数与方程思想.
专题四 函数与方程思想
在△ABC中,已知A>B>C,且A=2C,b=4,a+c=8,求a,c的长.
【例4】 解斜三角形是高考的热点内容,经常和三角化简、向量运算等联系在一起综合考查,既可能以选择题和填空题的方式也可能以解答题的形式进行考查,解答题的难度属于中低档的问题.
具体的命题过程有如下规律:
一是考查三角形的角的问题.求三角形的角常用到的工具有三角形内角和为180°,正、余弦定理及其变式,经常与三角化简求值联系在一起考查.
二是考查三角形的面积.三角形面积的处理途径比较多,需要根据条件,恰当的进行选择,实际上最终转化为三角形的边角问题解决.
命题趋势 三是对解三角形的综合问题的考查.一般题目给出边角满足的关系式,问题处理的重点是正、余弦定理的选择.需要熟练掌握正、余弦定理和三角形面积公式以及之间的联系,灵活应用二倍角公式、两角和与差公式等进行化简;不仅会利用方程思想求值,还要会利用函数思想讨论最值问题.
