人教高中数学必修一第一章集合与函数的概念复习(共34张PPT)
文档属性
| 名称 | 人教高中数学必修一第一章集合与函数的概念复习(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 747.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-02 23:39:37 | ||
图片预览










文档简介
(共35张PPT)
第一章 章末归纳总结
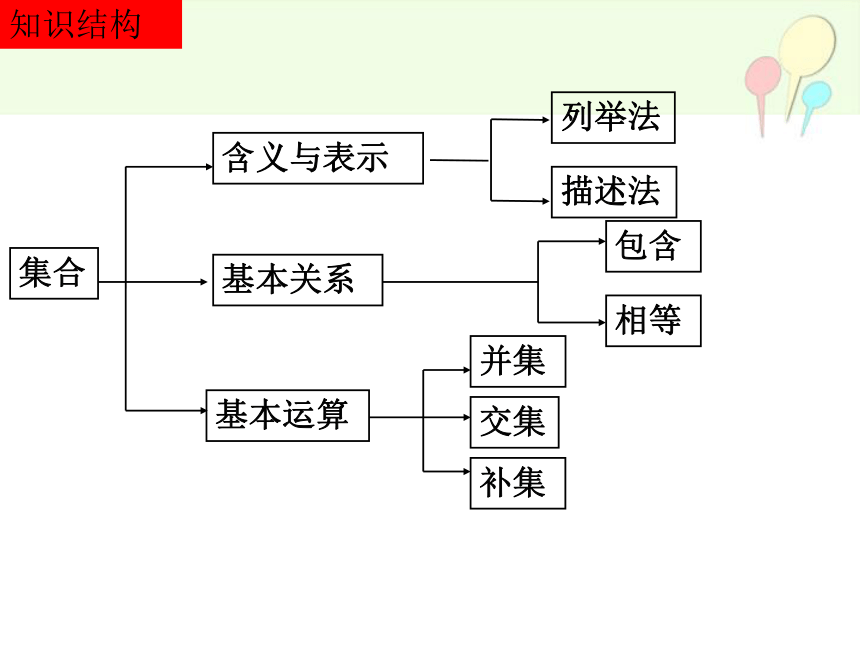
集合
集合
含义与表示
基本关系
基本运算
交集
并集
补集
包含
相等
列举法
描述法
知识结构
集合的含义与表示
2.集合:把一些元素组成的 叫做集合(简称为集),通常用 表示.
研究对象
总体
小写拉丁字母a,b,c …
大写拉丁字母A,B,C …
3.集合中元素的特征: .
确定性、互异性、无序性
4.集合相等:只要构成两个集合的元素是 ,我们就称这两个集合是 .
一样的
相等的
1.元素:一般地,我们把 统称为元素,通常
用 表示.
5.元素与集合的关系:
集合中元素的特性及其应用
例1:若一个集合中含有三个元素0,x?+2x, x+2。求x满足的条件。(p2)
注意元素的互异性
总结:集合中的元素具有确定性,互异性,无序性,在解含有参数的集合的问题时,要注意解题后的代入检验.
自然数集(非负整数集):记作
正整数集:记作 或
整数集:记作
有理数集:记作
实数集:记作
N
Z
Q
R
6.常用数集及表示符号
1、列举法:把集合中的元素 出来,并放在{ }内
2、描述法:用文字或公式等描述出元素的 ,并放在{x| }内
3.图示法:Venn图 4.自然语言
(二)集合的表示
一一列举
共同特征
例3:若方程ax?+bx+1=0的解集与集合A中的元素为1、2,求a,b的值。(p4)
二、集合间的基本关系
都是集合B的元素,我们称A为B的子集.
3.集合相等:
4.空集:
2n
2n-1
2n-2
2.真子 集:
5.若集合中元素有n个,则其子集个数为
真子集个数为
非空真子集个数为
1.子集:
对于两个集合A,B如果集合A中的任何一个元素
规定空集是任何集合的子集,是任何非空集合的
真子集
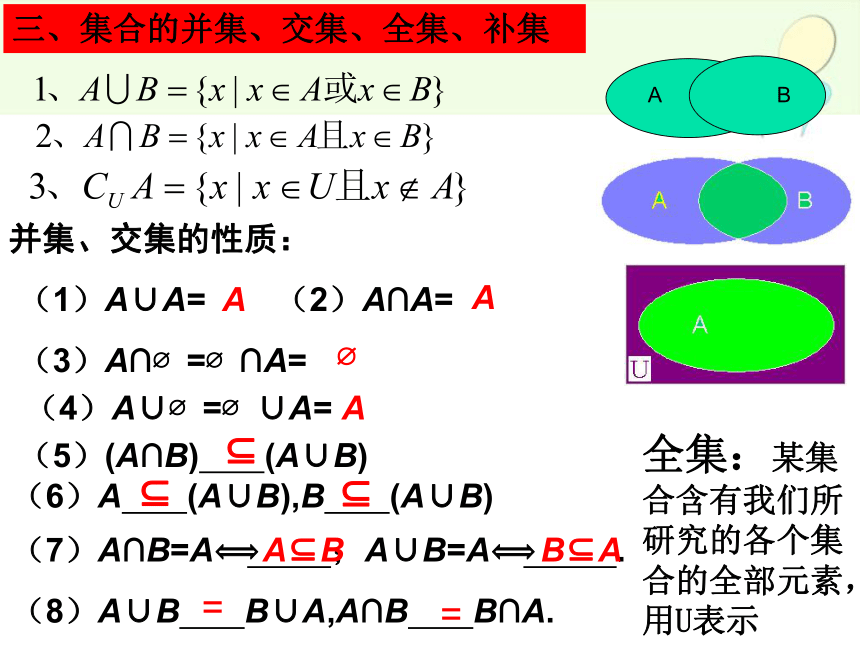
三、集合的并集、交集、全集、补集
全集:某集合含有我们所研究的各个集合的全部元素,用U表示
A
B
(1)A∪A=
(4)A∪?=?∪A=
(2)A∩A=
(3)A∩?=?∩A=
(6)A (A∪B),B (A∪B)
(5)(A∩B) (A∪B)
(8)A∪B B∪A,A∩B B∩A.
(7)A∩B=A? ;A∪B=A? .
并集、交集的性质:
A
A
?
A
?
?
?
=
=
A?B
B?A
补集的性质:
A∪(?UA)= ;A∩(?UA)= ;?U(?UA)= ;
?U(A∩B)= ;
?U(A∪B)= .
U
?
A
(?UA)∪(?UB)
(?UA)∩(?UB)
3.注意空集的特殊性
题型
集合实际应用
例6:向50名学生调查对A、B两事件的态度,有如下结果:赞成A的人数是30,其余的不赞成,赞成B的人数是33,其余的不赞成;另外,对A、B都不赞成的学生比对A、B都赞成的学生数的三分之一多1人.问对A、B都赞成的学生和都不赞成的学生各多少人?
分析:
画出韦恩图,形象地表示出各数量关系的联系
解:
方法归纳:
解决这一类问题一般借用数形结合,借助于Venn 图,把抽象的数学语言与直观的图形结合起来
设A,B是非空的 ,如果按照某种确定的对应关系f,使对于集合A中的 ,在集合B中都有
和它对应,那么就称 为从集合A到集合B的一个函数.
记作:
函数的概念:
数集
任意一个数x
唯一确定的数f(x)
其中,x叫做 , A叫做函数的定义域,与x相对应的y值叫做 ,函数值的集合 叫做函数的值域.值域是集合B的子集.
自变量
x的取值范围
函数值
(1)函数的三要素: .
定义域、对应关系、值域
3.函数三种表示法:
解析法;列表法;图象法。
知识探究(二)区间
思考1:设a,b是两个实数,且a[a,+∞),(a,+∞), (-∞,a],(-∞,a).
思考2:将实数集R看成一个大区间,怎样用区间表示实数集R?
(-∞,+∞)
上述知识内容总结成下表:
这里的实数a与b都叫做相应区间的端点.
a
b
a
b
a
b
数轴表示
定义
符号
名称
[ a, b ]
闭区间
( a, b )
[ a, b )
开区间
半开半闭
区间
半开半闭
区间
{x|a≤x≤b}
{x|a{x|a≤x{x|a( a, b ]
a
b
例题讲解
1.求函数的定义域应注意:
(2)f(x)是分式,则分母不为0;
(1)f(x)是整式,则定义域是R;
(3)偶次方根的被开方数非负;
(5)表格形式给出时,定义域就是表格中数的集合.
定义域
配方法
解:
求值域的方法
观察法通过对解析式的简单变形和观察,利用熟知的基本函数的值域,求出函数的值域.
分离常数法
例7 求函数
解:
反表示法
解:配方,画简图
增函数、减函数、单调函数是对定义域上的某个区间而言的
三、函数单调性
如果对于定义域I内某个区间D上的任意两个自变量x1、x2,当x1f(x2) ,那么就说函数在区间上是减函数。区间D叫做函数的减区间。
定义:一般地,设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量x1、x2
当x1增函数。区间D叫做函数的增区间。
3.最大(小)值的定义:
例5 画出函数f(x)=3x+2的图像,判断它的单调性,并加以证明.
解 作出f(x)=3x+2的图像.由图看出,函数的图在R上是上升的,函数是R上的增函数.
所以 f(x1)-f(x2)=(3x1+2)-(3x2+2)
=3(x1-x2),
任取x1,x2∈R,设x1取值
作差
变形
定号
证明:
判断 下结论
四、函数的奇偶性
3.奇函数和偶函数的必要条件:
注:要判断函数的奇偶性,首先要看其定义域是否关于原点对称!
定义域关于原点对称.
奇(偶)函数的一些特征
1.若函数f(x)是奇函数,且在x=0处有定义,则f(0)=0.
2.奇函数图像关于原点对称,且在对称的区间上单调性一致。
3.偶函数图像关于y轴对称,且在对称的区间上单调性相反。
例题讲解
例题讲解
练习
练习
练习
第一章 章末归纳总结
集合
集合
含义与表示
基本关系
基本运算
交集
并集
补集
包含
相等
列举法
描述法
知识结构
集合的含义与表示
2.集合:把一些元素组成的 叫做集合(简称为集),通常用 表示.
研究对象
总体
小写拉丁字母a,b,c …
大写拉丁字母A,B,C …
3.集合中元素的特征: .
确定性、互异性、无序性
4.集合相等:只要构成两个集合的元素是 ,我们就称这两个集合是 .
一样的
相等的
1.元素:一般地,我们把 统称为元素,通常
用 表示.
5.元素与集合的关系:
集合中元素的特性及其应用
例1:若一个集合中含有三个元素0,x?+2x, x+2。求x满足的条件。(p2)
注意元素的互异性
总结:集合中的元素具有确定性,互异性,无序性,在解含有参数的集合的问题时,要注意解题后的代入检验.
自然数集(非负整数集):记作
正整数集:记作 或
整数集:记作
有理数集:记作
实数集:记作
N
Z
Q
R
6.常用数集及表示符号
1、列举法:把集合中的元素 出来,并放在{ }内
2、描述法:用文字或公式等描述出元素的 ,并放在{x| }内
3.图示法:Venn图 4.自然语言
(二)集合的表示
一一列举
共同特征
例3:若方程ax?+bx+1=0的解集与集合A中的元素为1、2,求a,b的值。(p4)
二、集合间的基本关系
都是集合B的元素,我们称A为B的子集.
3.集合相等:
4.空集:
2n
2n-1
2n-2
2.真子 集:
5.若集合中元素有n个,则其子集个数为
真子集个数为
非空真子集个数为
1.子集:
对于两个集合A,B如果集合A中的任何一个元素
规定空集是任何集合的子集,是任何非空集合的
真子集
三、集合的并集、交集、全集、补集
全集:某集合含有我们所研究的各个集合的全部元素,用U表示
A
B
(1)A∪A=
(4)A∪?=?∪A=
(2)A∩A=
(3)A∩?=?∩A=
(6)A (A∪B),B (A∪B)
(5)(A∩B) (A∪B)
(8)A∪B B∪A,A∩B B∩A.
(7)A∩B=A? ;A∪B=A? .
并集、交集的性质:
A
A
?
A
?
?
?
=
=
A?B
B?A
补集的性质:
A∪(?UA)= ;A∩(?UA)= ;?U(?UA)= ;
?U(A∩B)= ;
?U(A∪B)= .
U
?
A
(?UA)∪(?UB)
(?UA)∩(?UB)
3.注意空集的特殊性
题型
集合实际应用
例6:向50名学生调查对A、B两事件的态度,有如下结果:赞成A的人数是30,其余的不赞成,赞成B的人数是33,其余的不赞成;另外,对A、B都不赞成的学生比对A、B都赞成的学生数的三分之一多1人.问对A、B都赞成的学生和都不赞成的学生各多少人?
分析:
画出韦恩图,形象地表示出各数量关系的联系
解:
方法归纳:
解决这一类问题一般借用数形结合,借助于Venn 图,把抽象的数学语言与直观的图形结合起来
设A,B是非空的 ,如果按照某种确定的对应关系f,使对于集合A中的 ,在集合B中都有
和它对应,那么就称 为从集合A到集合B的一个函数.
记作:
函数的概念:
数集
任意一个数x
唯一确定的数f(x)
其中,x叫做 , A叫做函数的定义域,与x相对应的y值叫做 ,函数值的集合 叫做函数的值域.值域是集合B的子集.
自变量
x的取值范围
函数值
(1)函数的三要素: .
定义域、对应关系、值域
3.函数三种表示法:
解析法;列表法;图象法。
知识探究(二)区间
思考1:设a,b是两个实数,且a
思考2:将实数集R看成一个大区间,怎样用区间表示实数集R?
(-∞,+∞)
上述知识内容总结成下表:
这里的实数a与b都叫做相应区间的端点.
a
b
a
b
a
b
数轴表示
定义
符号
名称
[ a, b ]
闭区间
( a, b )
[ a, b )
开区间
半开半闭
区间
半开半闭
区间
{x|a≤x≤b}
{x|a
a
b
例题讲解
1.求函数的定义域应注意:
(2)f(x)是分式,则分母不为0;
(1)f(x)是整式,则定义域是R;
(3)偶次方根的被开方数非负;
(5)表格形式给出时,定义域就是表格中数的集合.
定义域
配方法
解:
求值域的方法
观察法通过对解析式的简单变形和观察,利用熟知的基本函数的值域,求出函数的值域.
分离常数法
例7 求函数
解:
反表示法
解:配方,画简图
增函数、减函数、单调函数是对定义域上的某个区间而言的
三、函数单调性
如果对于定义域I内某个区间D上的任意两个自变量x1、x2,当x1
定义:一般地,设函数f(x)的定义域为I:
如果对于定义域I内某个区间D上的任意两个自变量x1、x2
当x1
3.最大(小)值的定义:
例5 画出函数f(x)=3x+2的图像,判断它的单调性,并加以证明.
解 作出f(x)=3x+2的图像.由图看出,函数的图在R上是上升的,函数是R上的增函数.
所以 f(x1)-f(x2)=(3x1+2)-(3x2+2)
=3(x1-x2),
任取x1,x2∈R,设x1
作差
变形
定号
证明:
判断 下结论
四、函数的奇偶性
3.奇函数和偶函数的必要条件:
注:要判断函数的奇偶性,首先要看其定义域是否关于原点对称!
定义域关于原点对称.
奇(偶)函数的一些特征
1.若函数f(x)是奇函数,且在x=0处有定义,则f(0)=0.
2.奇函数图像关于原点对称,且在对称的区间上单调性一致。
3.偶函数图像关于y轴对称,且在对称的区间上单调性相反。
例题讲解
例题讲解
练习
练习
练习
