人教版八年级数学上册第十三章 轴对称 13.3 等腰三角形的性质 课件(共54张ppt)
文档属性
| 名称 | 人教版八年级数学上册第十三章 轴对称 13.3 等腰三角形的性质 课件(共54张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-02 23:23:20 | ||
图片预览








文档简介
(共54张PPT)
13.3? 等腰三角形的性质
生活中的等腰三角形
生活中的等腰三角形
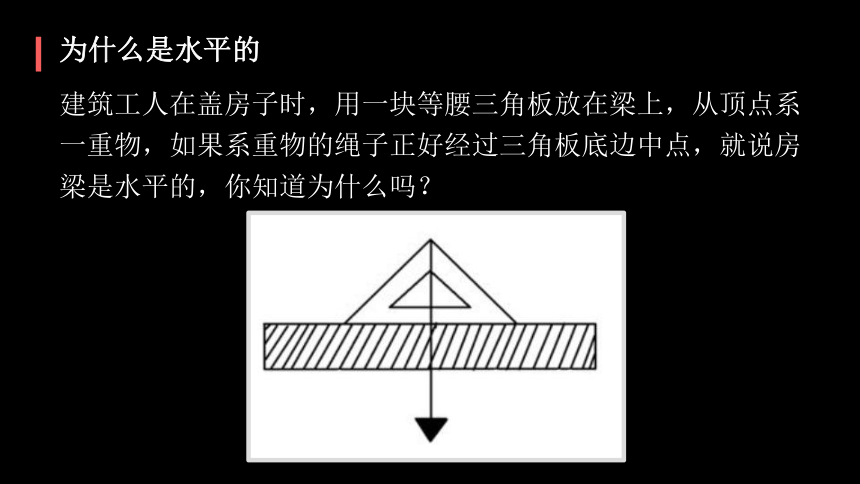
为什么是水平的
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?
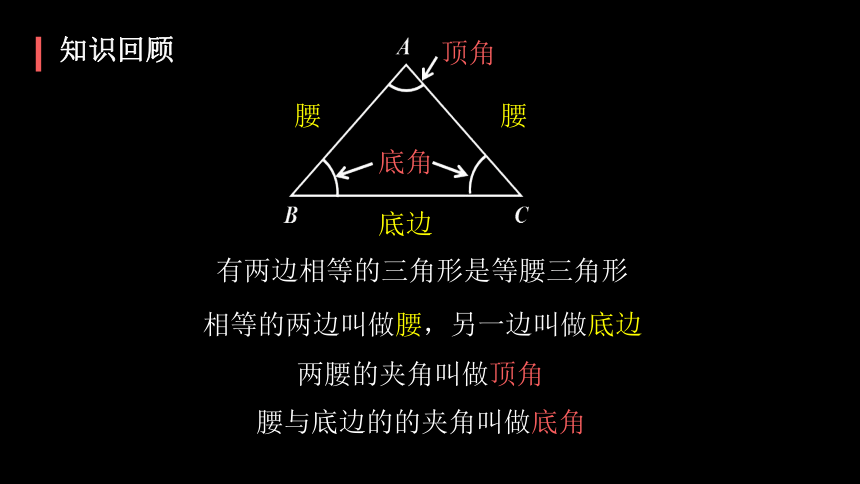
有两边相等的三角形是等腰三角形
知识回顾
相等的两边叫做腰,另一边叫做底边
腰
腰
底边
两腰的夹角叫做顶角
顶角
腰与底边的的夹角叫做底角
底角
知识回顾
1.等腰三角形一腰为3cm,底为4cm,则它的周长是 _______;
2.等腰三角形一边长为3cm,另一边长为4cm,则它的周长是 _______________;
3.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是_______________.
10cm
10cm或11cm
19cm
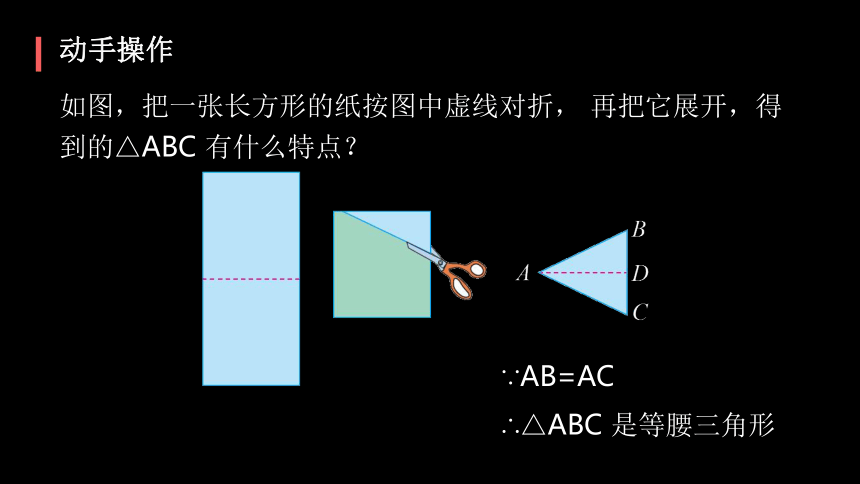
动手操作
如图,把一张长方形的纸按图中虚线对折, 再把它展开,得到的△ABC?有什么特点?
∵AB=AC
∴△ABC 是等腰三角形
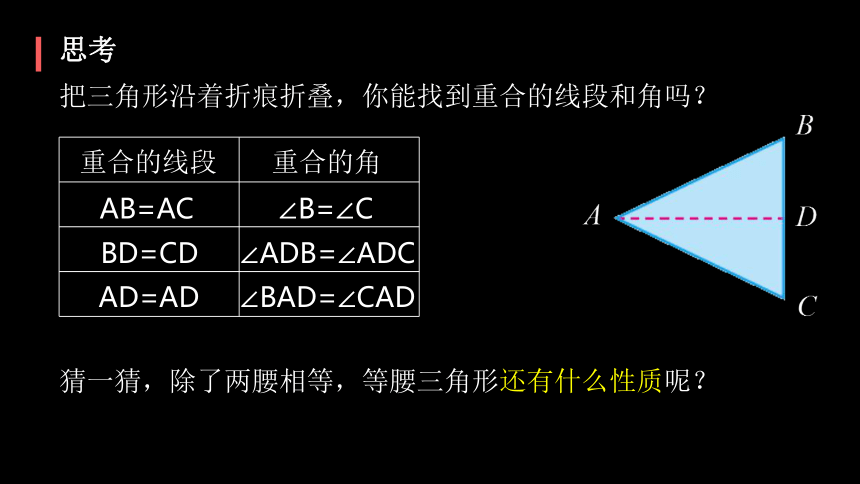
把三角形沿着折痕折叠,你能找到重合的线段和角吗?
思考
重合的线段
重合的角
AB=AC
∠B=∠C
BD=CD
∠ADB=∠ADC
AD=AD
∠BAD=∠CAD
猜一猜,除了两腰相等,等腰三角形还有什么性质呢?
猜想与证明
等腰三角形的两个底角相等
怎么证明呢?
先变成符号形式
已知:△ABC 中,AB=AC.
求证:∠B=∠C.
如何证明两个角相等呢?
可以证明三角形全等
如何构造全等三角形呢?
AD是中线or高or角平分线?
证法一:作底边上的中线
已知:△ABC 中,AB=AC.
求证:∠B=∠C.
证明:
作底边的中线AD,则BD=CD
在△BAD和△CAD中
AB=AC ( 已知 )
BD=CD ( 已作 )
AD=AD (公共边)?
∴ △BAD ≌ △CAD(SSS)
∴ ∠ B= ∠C (全等三角形的对应角相等)
D
证法二:作顶角的平分线
已知:△ABC 中,AB=AC.
求证:∠B=∠C.
证明:
作顶角的平分线AD,则∠BAD=∠CAD
在△BAD和△CAD中
AB=AC ( 已知 )
∠BAD=∠CAD ( 已作 )
AD=AD (公共边)?
∴ △BAD ≌ △CAD(SAS)
∴ ∠ B= ∠C (全等三角形的对应角相等)
D
证法三:作底边的高线
已知:△ABC中,AB=AC.
求证:∠B=∠C.
证明:
作底边的高线AD,则∠ADB=∠ADC=90°
在Rt△BAD和Rt△CAD中
AB=AC ( 已知 )
AD=AD (公共边)
∴ Rt△BAD ≌ Rt△CAD(HL)
∴ ∠ B= ∠C(全等三角形的对应角相等)
D
归纳总结
等腰三角形的性质1:
等腰三角形的两个底角相等
这个性质在证明中怎么写过程呢?
在△ABC 中,
∵ AC =AB( 已知)
∴ ∠B=∠C (等边对等角)
简称为“等边对等角”
思考
通过刚才的证明,除了能得到∠B=∠C,你还能发现什么?
重合的线段
重合的角
AB=AC
∠B=∠C
BD=CD
∠ADB=∠ADC
AD=AD
∠BAD=∠CAD
AD同时是底边BC上的中线,高和角平分线.
猜想
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
如何把这个命题转化为符号形式呢?
得写三个
(1)如图,∠1=∠2,AB=AC.? ?
? ? ? ? ? 求证:AD⊥BC,BD=CD.
(2)如图,BD=CD,AB=AC.? ?
? ? ? ? ? 求证:AD⊥BC,∠1=∠2.
(3)如图,AD⊥BC,AB=AC.
? 求证:BD=CD,∠1=∠2.
证明
(3)如图,AD⊥BC,AB=AC.
求证:BD=CD,∠1=∠2.
证明:在△ABD 和△ACD中
AB=AC
∠1=∠2
AD=AD
∴△ABD ≌△ACD(SAS)
∴∠ADB=∠ADC,BD=CD
又∵∠ADB+∠ADC=180°
∴∠ADB=∠ADC=90°,即AD⊥BC
证明
(2)如图,BD=CD,AB=AC.??
? ? ? ? ? 求证:AD⊥BC,∠1=∠2.
证明:在△ABD 和△ACD 中
AB=AC
BD=CD
AD=AD
∴△ABD ≌△ACD(SSS)
∴∠ADB=∠ADC,∠1=∠2
又∵∠ADB+∠ADC=180°
∴∠ADB=∠ADC=90°,即AD⊥BC
证明
(3)如图,AD⊥BC,AB=AC.
? 求证:BD=CD,∠1=∠2.
证明:在Rt△ABD 和Rt△ACD中
AB=AC
AD=AD
∴Rt△ABD ≌Rt△ACD(HL)
∴BD=CD,∠1=∠2
归纳总结
等腰三角形的性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
简称为“三线合一”
这“三线”所在的直线也是等腰三角形的对称轴
注意事项
作出等腰三角形腰上的中线,角平分线,高
它们重合吗?
显然不重合
三线合一指的是底边上
的三线合一腰的三线不一定合一
书写规范
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
“三线合一”有三种解读方式
等腰三角形的顶角平分线,
既是底边上的中线,又是底边上的高.
应用的时候怎么写过程呢?
∵AB=AC,∠1=∠2
∴BD=CD, AD⊥BC
书写规范
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
“三线合一”有三种解读方式
方式二:
等腰三角形的底边上的中线,
既是顶角平分线,又是底边上的高.
应用的时候怎么写过程呢?
∵AB=AC, BD=CD
∴∠1=∠2, AD⊥BC
书写规范
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
“三线合一”有三种解读方式
方式三:
等腰三角形的底边上的高,
既是顶角平分线,又是底边上的中线.
应用的时候怎么写过程呢?
∵AB=AC, AD⊥BC
∴∠1=∠2,BD=CD
例题
如图,△ABC 中, AB =AC,∠A =36°, 则∠B =________.
答案:72°.
例题
如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
技巧:看到等腰,就把等角标出来.
练习
如图,△ABC 中, AB =AC, ∠B =36°,则∠A =______.
答案:72°.
练习
判断:
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角或者直角、钝角都可以.
3.等腰三角形的顶角平分线一定垂直底边.
4.等腰三角形的角平分线、中线和高互相重合.
5.等腰三角形底边上的中线一定平分顶角.
练习
已知:如图,△ABC 中,∠ABC=50°,∠ACB=80°,延长 CB 至 D,使BD=BA,延长 BC 至 E,使 CE = CA . 连结 AD、AE . 求∠D、∠E、∠DAE 的度数.
答案:115°.
练习
在△ABC 中,AB=AD=DC,∠BAD=28° ,求∠B和∠C 的度数.
答案:76°或38°.
练习
如图,在△ABC 中,D为AB上的一点,E为BC上一点,且AC=CD=BD=BE,∠A=50° ,则∠CDE 的度数为_______.
答案:52.5°.
练习
答案:20°.
如图,AB=AC,∠BAC=100°,若MP,NQ 分别垂直平分AB,AC,则∠PAQ 的度数为? ?? ?? ? ?.
等边对等角多解问题
已知等腰三角形的一个内角为70°,则它的另外两个内角的度数分别是_________.
提示:要分类讨论.
答案:70°,40°或55°,55°.
等边对等角多解问题
等腰三角形一个角为110°,它的另外两个角为________.
答案:35°,35°.
怎么解“等边对等角多解问题”?
等边对等角多解问题
为什么是水平的
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?
由“三线合一”可知绳子一定会垂直房梁,而绳子肯定是竖直的,所以房梁是水平的.
例题
已知:如图,房屋的顶角∠BAC=100 ?,,过屋顶A的立柱AD⊥BC ,屋椽AB=AC.求顶架上∠B、∠C、∠BAD、∠CAD 的度数.
答案:40°,40°,50°,50°.
练习
如图,在△ABC中,AB=AC,D是BC 边上的中点,∠B=30°,求∠1和∠ADC 的度数.
提示:60°,90°.
练习
如图,已知在△ABC 中,AB=AC,点D是BC 的中点,DE⊥AB于E,DF⊥AC于F.求证:DE=DF.
提示:AD是角平分线.
练习
如图,在△ABC 中,AB = AC,AD 是 BC 边上的中线,BE ⊥ AC 于点 E.求证:∠CBE = ∠BAD.
提示:先把图中相等和互余的角标记出来.
练习
已知,如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有(? ?)个
(1)AD平分∠EDF;
(2)△EBD≌△FCD;
(3)BD=CD;
(4)DE⊥AB.
A.1个
B.2个
C.3个
D.4个
C
练习
1.如图,在下列等腰三角形中,分别求出它们的底角的度数.
练习
2.如图,△ABC 是等腰直角三角形(AB =AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的线段 .
练习
3.如图,在△ABC 中,AB=AD=DC,∠BAD=26°.求∠B 和∠C 的度数.
与等腰三角形有关的证明
如图,点 D,E 在△ABC 的边 BC 上,AD = AE,AB = AC,求证:BD = EC.
提示:证明△ABD ≌△AEC 或作BC 的中线.
与等腰三角形有关的证明
如图:△ABC中,AB=AC,AD 和BE是高,它们相交于点H,且AE=BE.求证:AH=2BD.
提示:证明△AHE ≌△CBE.
与等腰三角形有关的证明
如图,已知△ABC 中,AB=AC,F 在AC上,在BA的延长线上截取AE=AF.求证:ED⊥BC.
提示:想想图中两个等腰三角形的顶角有什么关系,底角有什么关系.
大边对大角
已知:△ABC 中,AB>AC,求证:∠C>∠B.
提示:构造等腰.
顶角的外角与底角的关系
如图,C,E 和 B,D,F 分别在∠GAH 的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF 的度数是__________.
答案:90°.
顶角的外角与底角的关系
如图,在第1个? ? ? ? ? ? 中,∠B=20°,AB=? ? ? ?,在? ? ? ? 上取
一点C,延长? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?在? ? ? ? 上取一点D,
延长? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?... ,...,按此作法进行下去,第n个
三角形的以? ? ? 为顶点的内角的度数为? ? ? ? ? ??.
顶角差与底角差的关系
如图,已知AB = AC,AD = AE,∠BAD和∠CDE有什么关系?
提示:试一试“设而不求”的技巧.
答案:∠BAD=2∠CDE.
总结
这节课我们学到了什么?
等腰三角形的性质1:
等腰三角形的两个底角相等
简称为“等边对等角”
总结
这节课我们还学到了什么?
等腰三角形的性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
简称为“三线合一”
这“三线”所在的直线也是等腰三角形的对称轴
怎么证明“等边对等角”?
怎么利用“等边对等角”的性质求角度.
等边对等角
怎么证明“三线合一”?
怎么利用“三线合一”的性质求角度.
等腰三角形三线合一
13.3? 等腰三角形的性质
生活中的等腰三角形
生活中的等腰三角形
为什么是水平的
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?
有两边相等的三角形是等腰三角形
知识回顾
相等的两边叫做腰,另一边叫做底边
腰
腰
底边
两腰的夹角叫做顶角
顶角
腰与底边的的夹角叫做底角
底角
知识回顾
1.等腰三角形一腰为3cm,底为4cm,则它的周长是 _______;
2.等腰三角形一边长为3cm,另一边长为4cm,则它的周长是 _______________;
3.等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是_______________.
10cm
10cm或11cm
19cm
动手操作
如图,把一张长方形的纸按图中虚线对折, 再把它展开,得到的△ABC?有什么特点?
∵AB=AC
∴△ABC 是等腰三角形
把三角形沿着折痕折叠,你能找到重合的线段和角吗?
思考
重合的线段
重合的角
AB=AC
∠B=∠C
BD=CD
∠ADB=∠ADC
AD=AD
∠BAD=∠CAD
猜一猜,除了两腰相等,等腰三角形还有什么性质呢?
猜想与证明
等腰三角形的两个底角相等
怎么证明呢?
先变成符号形式
已知:△ABC 中,AB=AC.
求证:∠B=∠C.
如何证明两个角相等呢?
可以证明三角形全等
如何构造全等三角形呢?
AD是中线or高or角平分线?
证法一:作底边上的中线
已知:△ABC 中,AB=AC.
求证:∠B=∠C.
证明:
作底边的中线AD,则BD=CD
在△BAD和△CAD中
AB=AC ( 已知 )
BD=CD ( 已作 )
AD=AD (公共边)?
∴ △BAD ≌ △CAD(SSS)
∴ ∠ B= ∠C (全等三角形的对应角相等)
D
证法二:作顶角的平分线
已知:△ABC 中,AB=AC.
求证:∠B=∠C.
证明:
作顶角的平分线AD,则∠BAD=∠CAD
在△BAD和△CAD中
AB=AC ( 已知 )
∠BAD=∠CAD ( 已作 )
AD=AD (公共边)?
∴ △BAD ≌ △CAD(SAS)
∴ ∠ B= ∠C (全等三角形的对应角相等)
D
证法三:作底边的高线
已知:△ABC中,AB=AC.
求证:∠B=∠C.
证明:
作底边的高线AD,则∠ADB=∠ADC=90°
在Rt△BAD和Rt△CAD中
AB=AC ( 已知 )
AD=AD (公共边)
∴ Rt△BAD ≌ Rt△CAD(HL)
∴ ∠ B= ∠C(全等三角形的对应角相等)
D
归纳总结
等腰三角形的性质1:
等腰三角形的两个底角相等
这个性质在证明中怎么写过程呢?
在△ABC 中,
∵ AC =AB( 已知)
∴ ∠B=∠C (等边对等角)
简称为“等边对等角”
思考
通过刚才的证明,除了能得到∠B=∠C,你还能发现什么?
重合的线段
重合的角
AB=AC
∠B=∠C
BD=CD
∠ADB=∠ADC
AD=AD
∠BAD=∠CAD
AD同时是底边BC上的中线,高和角平分线.
猜想
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
如何把这个命题转化为符号形式呢?
得写三个
(1)如图,∠1=∠2,AB=AC.? ?
? ? ? ? ? 求证:AD⊥BC,BD=CD.
(2)如图,BD=CD,AB=AC.? ?
? ? ? ? ? 求证:AD⊥BC,∠1=∠2.
(3)如图,AD⊥BC,AB=AC.
? 求证:BD=CD,∠1=∠2.
证明
(3)如图,AD⊥BC,AB=AC.
求证:BD=CD,∠1=∠2.
证明:在△ABD 和△ACD中
AB=AC
∠1=∠2
AD=AD
∴△ABD ≌△ACD(SAS)
∴∠ADB=∠ADC,BD=CD
又∵∠ADB+∠ADC=180°
∴∠ADB=∠ADC=90°,即AD⊥BC
证明
(2)如图,BD=CD,AB=AC.??
? ? ? ? ? 求证:AD⊥BC,∠1=∠2.
证明:在△ABD 和△ACD 中
AB=AC
BD=CD
AD=AD
∴△ABD ≌△ACD(SSS)
∴∠ADB=∠ADC,∠1=∠2
又∵∠ADB+∠ADC=180°
∴∠ADB=∠ADC=90°,即AD⊥BC
证明
(3)如图,AD⊥BC,AB=AC.
? 求证:BD=CD,∠1=∠2.
证明:在Rt△ABD 和Rt△ACD中
AB=AC
AD=AD
∴Rt△ABD ≌Rt△ACD(HL)
∴BD=CD,∠1=∠2
归纳总结
等腰三角形的性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
简称为“三线合一”
这“三线”所在的直线也是等腰三角形的对称轴
注意事项
作出等腰三角形腰上的中线,角平分线,高
它们重合吗?
显然不重合
三线合一指的是底边上
的三线合一腰的三线不一定合一
书写规范
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
“三线合一”有三种解读方式
等腰三角形的顶角平分线,
既是底边上的中线,又是底边上的高.
应用的时候怎么写过程呢?
∵AB=AC,∠1=∠2
∴BD=CD, AD⊥BC
书写规范
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
“三线合一”有三种解读方式
方式二:
等腰三角形的底边上的中线,
既是顶角平分线,又是底边上的高.
应用的时候怎么写过程呢?
∵AB=AC, BD=CD
∴∠1=∠2, AD⊥BC
书写规范
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
“三线合一”有三种解读方式
方式三:
等腰三角形的底边上的高,
既是顶角平分线,又是底边上的中线.
应用的时候怎么写过程呢?
∵AB=AC, AD⊥BC
∴∠1=∠2,BD=CD
例题
如图,△ABC 中, AB =AC,∠A =36°, 则∠B =________.
答案:72°.
例题
如图,在△ABC中 ,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数.
技巧:看到等腰,就把等角标出来.
练习
如图,△ABC 中, AB =AC, ∠B =36°,则∠A =______.
答案:72°.
练习
判断:
1.等腰三角形的顶角一定是锐角.
2.等腰三角形的底角可能是锐角或者直角、钝角都可以.
3.等腰三角形的顶角平分线一定垂直底边.
4.等腰三角形的角平分线、中线和高互相重合.
5.等腰三角形底边上的中线一定平分顶角.
练习
已知:如图,△ABC 中,∠ABC=50°,∠ACB=80°,延长 CB 至 D,使BD=BA,延长 BC 至 E,使 CE = CA . 连结 AD、AE . 求∠D、∠E、∠DAE 的度数.
答案:115°.
练习
在△ABC 中,AB=AD=DC,∠BAD=28° ,求∠B和∠C 的度数.
答案:76°或38°.
练习
如图,在△ABC 中,D为AB上的一点,E为BC上一点,且AC=CD=BD=BE,∠A=50° ,则∠CDE 的度数为_______.
答案:52.5°.
练习
答案:20°.
如图,AB=AC,∠BAC=100°,若MP,NQ 分别垂直平分AB,AC,则∠PAQ 的度数为? ?? ?? ? ?.
等边对等角多解问题
已知等腰三角形的一个内角为70°,则它的另外两个内角的度数分别是_________.
提示:要分类讨论.
答案:70°,40°或55°,55°.
等边对等角多解问题
等腰三角形一个角为110°,它的另外两个角为________.
答案:35°,35°.
怎么解“等边对等角多解问题”?
等边对等角多解问题
为什么是水平的
建筑工人在盖房子时,用一块等腰三角板放在梁上,从顶点系一重物,如果系重物的绳子正好经过三角板底边中点,就说房梁是水平的,你知道为什么吗?
由“三线合一”可知绳子一定会垂直房梁,而绳子肯定是竖直的,所以房梁是水平的.
例题
已知:如图,房屋的顶角∠BAC=100 ?,,过屋顶A的立柱AD⊥BC ,屋椽AB=AC.求顶架上∠B、∠C、∠BAD、∠CAD 的度数.
答案:40°,40°,50°,50°.
练习
如图,在△ABC中,AB=AC,D是BC 边上的中点,∠B=30°,求∠1和∠ADC 的度数.
提示:60°,90°.
练习
如图,已知在△ABC 中,AB=AC,点D是BC 的中点,DE⊥AB于E,DF⊥AC于F.求证:DE=DF.
提示:AD是角平分线.
练习
如图,在△ABC 中,AB = AC,AD 是 BC 边上的中线,BE ⊥ AC 于点 E.求证:∠CBE = ∠BAD.
提示:先把图中相等和互余的角标记出来.
练习
已知,如图,△ABC中,AB=AC,AD是角平分线,BE=CF,则下列说法正确的有(? ?)个
(1)AD平分∠EDF;
(2)△EBD≌△FCD;
(3)BD=CD;
(4)DE⊥AB.
A.1个
B.2个
C.3个
D.4个
C
练习
1.如图,在下列等腰三角形中,分别求出它们的底角的度数.
练习
2.如图,△ABC 是等腰直角三角形(AB =AC,∠BAC =90°),AD 是底边BC 上的高,标出∠B,∠C,∠BAD,∠DAC 的度数,并写出图中所有相等的线段 .
练习
3.如图,在△ABC 中,AB=AD=DC,∠BAD=26°.求∠B 和∠C 的度数.
与等腰三角形有关的证明
如图,点 D,E 在△ABC 的边 BC 上,AD = AE,AB = AC,求证:BD = EC.
提示:证明△ABD ≌△AEC 或作BC 的中线.
与等腰三角形有关的证明
如图:△ABC中,AB=AC,AD 和BE是高,它们相交于点H,且AE=BE.求证:AH=2BD.
提示:证明△AHE ≌△CBE.
与等腰三角形有关的证明
如图,已知△ABC 中,AB=AC,F 在AC上,在BA的延长线上截取AE=AF.求证:ED⊥BC.
提示:想想图中两个等腰三角形的顶角有什么关系,底角有什么关系.
大边对大角
已知:△ABC 中,AB>AC,求证:∠C>∠B.
提示:构造等腰.
顶角的外角与底角的关系
如图,C,E 和 B,D,F 分别在∠GAH 的两边上,且AB=BC=CD=DE=EF,若∠A=18°,则∠GEF 的度数是__________.
答案:90°.
顶角的外角与底角的关系
如图,在第1个? ? ? ? ? ? 中,∠B=20°,AB=? ? ? ?,在? ? ? ? 上取
一点C,延长? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?在? ? ? ? 上取一点D,
延长? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?... ,...,按此作法进行下去,第n个
三角形的以? ? ? 为顶点的内角的度数为? ? ? ? ? ??.
顶角差与底角差的关系
如图,已知AB = AC,AD = AE,∠BAD和∠CDE有什么关系?
提示:试一试“设而不求”的技巧.
答案:∠BAD=2∠CDE.
总结
这节课我们学到了什么?
等腰三角形的性质1:
等腰三角形的两个底角相等
简称为“等边对等角”
总结
这节课我们还学到了什么?
等腰三角形的性质2:
等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
简称为“三线合一”
这“三线”所在的直线也是等腰三角形的对称轴
怎么证明“等边对等角”?
怎么利用“等边对等角”的性质求角度.
等边对等角
怎么证明“三线合一”?
怎么利用“三线合一”的性质求角度.
等腰三角形三线合一
