人教版七年级数学上册第三章 一元一次方程 3.2.2 解一元一次方程之移项课件(共51张PPT)
文档属性
| 名称 | 人教版七年级数学上册第三章 一元一次方程 3.2.2 解一元一次方程之移项课件(共51张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-03 11:50:06 | ||
图片预览










文档简介
(共51张PPT)
3.2 解一元一次方程之移项
知识回顾
等式两边加(或减)同一个数(或式子),结果仍相等.?
等式两边乘同一个数(或式子),或除以同一个不为0的数(或式子),结果仍相等.
等式的性质1
等式的性质2
知识回顾
利用等式的性质解下列方程:
(1)x+2=1
(2)2x-3x=-7-8
答案:(1)x=-1;(2)x=15
问题
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
思考
你认为题中涉及到哪些相等关系?
如果每人分3本,则剩余20本
(1)学生人数×3+20=书本数
如果每人分4本,则还缺25本
(2)学生人数×4-25=书本数
设未知数
找等量关系
列方程
设这个班有x名学生.
每人分3本,共分出3x本,加上剩余的20本,这批书共 ________本.
每人分4本,需要4x本,减去缺的25本,
这批书共 ________ 本.
这批书的总数是一个定值,
表示它的两个等式相等
“表示同一个量的两个不同的式子相等”是一个基本的相等关系
3x+20
4x-25
思考
3x+20=4x-25
提问1:它与上节课遇到的方程有何不同?
方程的两边都有含x的项(3x与4x)
和不含字母的常数项(20与-25).
思考
提问2:如何才能使这个方程向x=a的形式转化?
3x+20=4x-25
(利用等式性质1)
3x+20-4x=4x-25-4x
(合并同类项)
3x+20-4x=-25
(利用等式性质1)
3x+20-4x-20=-25-20
(合并同类项)
3x-4x=-25-20
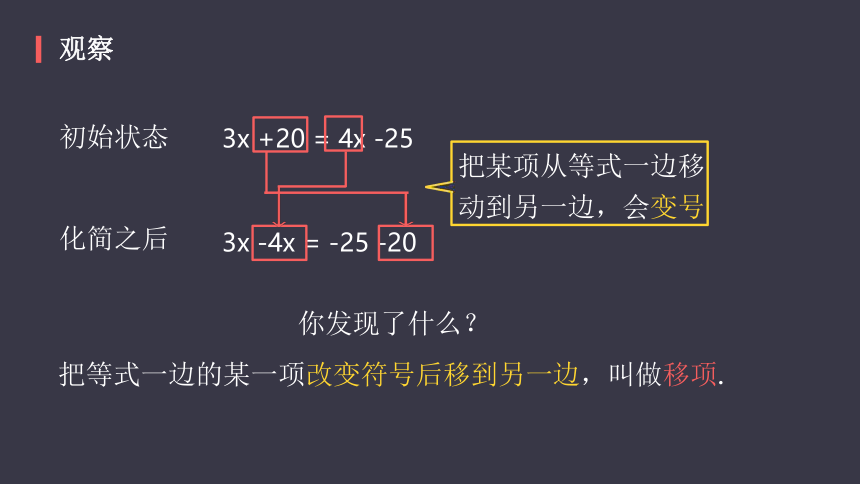
观察
初始状态
化简之后
3x +20 = 4x -25
3x -4x = -25 -20
把某项从等式一边移动到另一边,会变号
你发现了什么?
把等式一边的某一项改变符号后移到另一边,叫做移项.
由浅入深
两边都加上15,得
合并同类项,得
系数化为1,得
观察
思考:-15移到右边, ? ? ? ? ? ? ? ? ? ? ? ?发生了什么变化?
结论:
符号变了
4x-15=9
4x ? ? ? =9+15
由浅入深
两边都减去5x,得
合并同类项,得
系数化为1,得
观察
思考
5x移到左边,
发生了什么变化?
结论:符号变了?
2x ? ? ? ? =5x-21
2x?-5x?=-21
移项
4x -15 =9
4x ? ? ? ? =9 +15
2x ? ? ? ? = 5x -21
2x -5x =-21
把等式一边的某一项改变符号后移到另一边,叫做移项.
下面的框图表示解这个方程的具体过程
3x+20=4x-25
3x-4x =-25-20
-x =-45
x = 45
移项
合并同类项
系数化为1
思考
以上解方程“移项”的依据是什么?
等式的性质1
“移项”起了什么作用?
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,使方程更接近x=a的形式.
例题
解下列方程
解:移项,得
即2x=-4
系数化为1,得 x=-2
解:移项,得-3-3x=2-8
合并同类项,得-4x=-6
系数化为1,得
“移项”应注意什么?
移项要变号
5 + 2x = 1
2x = 1 - 5
8?- x = 3x + 2
?- x -3x = 2 - 8
例题
解下列方程
(1)3x+7=32-2x
答案:(1)x=5;(2)x=-8
(2)
移项训练
(1)方程3x-4=1,移项得3x=1______.
+4
(2)方程2x+3=5,移项得:2x=________.
5-3
(3)方程5x=x+1,移项得__________.
5x-x=1
(4)方程2x-7=-5x,移项得___________.
2x+5x=7
(5)方程4x=3x-8,移项得_____________.
4x-3x=-8
(6)方程x=3.5x-5x-9,移项得__________________.
x-3.5x+5x=-9
练习
解下列方程
答案:
(1)
(2)
(3)
(4)
(1) ? ? ? ? ? ? ? ?(2) ? ? ? ?;? (3) ? ? ? ? ? ? ? ? ; (4)
练习
解下列方程
答案:(1)y=-12;(2)x=16
(1)
(2)
练习
解下列方程
答案:
(1) x=-1 ;?(2) x=-8 ;?(3) x=-6 ;
解方程:
练习
答案:
练习
解方程:
答案:
一起来找茬
下面方程的解法对吗?如果不对,应怎样改正?
解方程:
移项,得
合并同类项,得
系数化为1,得
总结:移项一定要变号
练习
下面的移项对不对?如果不对,请改正?
(1)从5+2x=10,? ?得2x=10+5
(2)从3x=2x-5,? ? 得3x+2x=5
(3)从-2x+5=1-3x,? ? 得-2x+3x=1+5
练习
找出题中的错误,重新解方程。
......
......
......
①
②
③
例题
有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学?
解法一:设船有x条,则 ?
? ? ? ? ? ? ? ? 6(x+1)=9(x-1) ??
? ? ? ? ? ? ? ? 得出 x=5 ?
? ? ? ? ? ? ? ? 6× (5+1)=36(人) ?
答:这个班共有36人.
有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学?
解法二:设这个班共有同学x人,则
得出 x=36
答:这个班共有36人.
例题
例题
例4 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
答案:新工艺的废水排量是200t,?
? ? ? ? ? ?旧工艺的废水排量是500t.
练习
某学校组织学生共同种一批树,如果每人种5棵,则剩下3棵;如果每人种6棵,则缺3棵树苗,求参与种树的人数.
答案:参与种树的人数是6.
练习
天平的左边放2枚硬币和13克砝码,右边放6枚硬币和5克砝码,此时天平恰好平衡.每枚硬币的质量是多少克?
答案:每枚硬币的质量是2克.
练习
已知 2x+1 与 -12x+5 的值是相反数,求 x 的值.
答案:
练习
答案:
练习
1、解下列方程:
答案:(1)x=1;(2)x=-24
练习
2、王芳和李丽同时采摘樱桃,王芳平均每小时采摘8kg,李丽平均每小时采摘7kg.采摘结束王芳从她采摘的樱桃中取出0.25kg给了李丽,这时两人的樱桃一样多.她们采摘用了多少时间?
答案:她们采摘用了0.5小时.
总结
这节课我们学会了什么?
如何解形如?ax+b=cx+d?形式的方程
3x?+20=4x-25
移项要变号
3x?-4x?=-25-20
-x?=-45
x=45
合并同类项
系数化为1
目标:化为x=a的形式
移项
等式性质1
等式性质2
什么是移项?
移项要注意什么?
如何利用合并同类项和移项解一元一次方程?
合并同类项与移项
复习巩固
解下列方程:
复习巩固
举例说明解方程时怎样“移项”,你知道这样做的根据吗?
复习巩固
解下列方程:
用方程解答下列问题:
(1)x的5倍与2的和等于x的3倍与4的差,求x;
(2)y与-5的积等于y与5的和,求y.
复习巩固
复习巩固
小新出生时父亲28岁,现在父亲的年龄是小新年龄的3倍,求现在小新的年龄.
复习巩固
洗衣机厂今年计划生产洗衣机25500台,其中1型、2型、3型三种洗衣机的数量比为1 : 2 : 14,计划生产这三种洗衣机各多少台?
复习巩固
用一根长60m的绳子围出一个长方形,使它的长是宽的1.5倍,长和宽各应是多少?
综合运用
随着农业技术的现代化,节水型灌溉得到逐步推广.喷灌和滴灌是比漫灌节水的灌溉方式.灌溉三块同样大的实验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式.后两种方式用水量分别是漫灌的25%和15%.
(1) 设第一块实验田用水xt,则另两块实验田的用水量各如 ? ? ? ? 何表示?
(2) 如果三块实验田共用水420t,每块实验田各用水多少吨?
综合运用
某造纸厂为节约木材,大力扩大再生纸的生产,它去年10月生产再生纸2050t,这比它前年10月再生纸产量的2倍还多150t,它前年10月生产再生纸多少吨?
综合运用
把一根长100cm的木棍锯成两段,要使其中一段长比另一段长的2倍少5cm,应该在木棍的哪个位置锯开?
综合运用
几个人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种;如果每人种12棵,则缺6棵树苗.求参与种树的人数.
拓广探索
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为30?如果能,这三个数分别是多少?
拓广探索
一个两位数的个位上的数的3倍加1是十位上的数,个位上的数与十位上的数的和等于9,这个两位数是多少?
无限循环小数化分数
设0.7=x,由0.7=0.777...可知,10x=7.777...,所10x-x=7.
如何把像0.1,0.2,...,0.9 这样的无限循环小数化为分数形式?动手试一试.
形式即 ? ? ,一般地,任何一个无限循环小数都可以写为分数形式吗?如果
可以,应该怎样写呢?
我们知道分数 ? ? ?写为小数形式即0.3,反过来,无限循环小数?0.3 写为分数
先以无限循环小数0.7为例进行讨论.
.
.
.
.
.
.
.
.
.
无限循环小数化分数
再以无限循环小数0.73为例,做进一步的讨论.
无限循环小数0.73=0.737373...,它的循环节有两位,类比上面的讨论可以想到如下的做法.
设0.73=x,由0.73=0.737373...可知100x=73.7373...,所以100x-x=73.
如何把像0.10,0.12,...,0.98这样的无限循环小数化为分数形式?动手试一试.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
无限循环小数化分数
如何把无限循环小数0.735,0.823 1化为分数形式?动手
试一试,并总结把无限循环小数化为分数形式的一般规律.
3.2 解一元一次方程之移项
知识回顾
等式两边加(或减)同一个数(或式子),结果仍相等.?
等式两边乘同一个数(或式子),或除以同一个不为0的数(或式子),结果仍相等.
等式的性质1
等式的性质2
知识回顾
利用等式的性质解下列方程:
(1)x+2=1
(2)2x-3x=-7-8
答案:(1)x=-1;(2)x=15
问题
把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本.这个班有多少学生?
思考
你认为题中涉及到哪些相等关系?
如果每人分3本,则剩余20本
(1)学生人数×3+20=书本数
如果每人分4本,则还缺25本
(2)学生人数×4-25=书本数
设未知数
找等量关系
列方程
设这个班有x名学生.
每人分3本,共分出3x本,加上剩余的20本,这批书共 ________本.
每人分4本,需要4x本,减去缺的25本,
这批书共 ________ 本.
这批书的总数是一个定值,
表示它的两个等式相等
“表示同一个量的两个不同的式子相等”是一个基本的相等关系
3x+20
4x-25
思考
3x+20=4x-25
提问1:它与上节课遇到的方程有何不同?
方程的两边都有含x的项(3x与4x)
和不含字母的常数项(20与-25).
思考
提问2:如何才能使这个方程向x=a的形式转化?
3x+20=4x-25
(利用等式性质1)
3x+20-4x=4x-25-4x
(合并同类项)
3x+20-4x=-25
(利用等式性质1)
3x+20-4x-20=-25-20
(合并同类项)
3x-4x=-25-20
观察
初始状态
化简之后
3x +20 = 4x -25
3x -4x = -25 -20
把某项从等式一边移动到另一边,会变号
你发现了什么?
把等式一边的某一项改变符号后移到另一边,叫做移项.
由浅入深
两边都加上15,得
合并同类项,得
系数化为1,得
观察
思考:-15移到右边, ? ? ? ? ? ? ? ? ? ? ? ?发生了什么变化?
结论:
符号变了
4x-15=9
4x ? ? ? =9+15
由浅入深
两边都减去5x,得
合并同类项,得
系数化为1,得
观察
思考
5x移到左边,
发生了什么变化?
结论:符号变了?
2x ? ? ? ? =5x-21
2x?-5x?=-21
移项
4x -15 =9
4x ? ? ? ? =9 +15
2x ? ? ? ? = 5x -21
2x -5x =-21
把等式一边的某一项改变符号后移到另一边,叫做移项.
下面的框图表示解这个方程的具体过程
3x+20=4x-25
3x-4x =-25-20
-x =-45
x = 45
移项
合并同类项
系数化为1
思考
以上解方程“移项”的依据是什么?
等式的性质1
“移项”起了什么作用?
通过移项,使等号左边仅含未知数的项,等号右边仅含常数的项,使方程更接近x=a的形式.
例题
解下列方程
解:移项,得
即2x=-4
系数化为1,得 x=-2
解:移项,得-3-3x=2-8
合并同类项,得-4x=-6
系数化为1,得
“移项”应注意什么?
移项要变号
5 + 2x = 1
2x = 1 - 5
8?- x = 3x + 2
?- x -3x = 2 - 8
例题
解下列方程
(1)3x+7=32-2x
答案:(1)x=5;(2)x=-8
(2)
移项训练
(1)方程3x-4=1,移项得3x=1______.
+4
(2)方程2x+3=5,移项得:2x=________.
5-3
(3)方程5x=x+1,移项得__________.
5x-x=1
(4)方程2x-7=-5x,移项得___________.
2x+5x=7
(5)方程4x=3x-8,移项得_____________.
4x-3x=-8
(6)方程x=3.5x-5x-9,移项得__________________.
x-3.5x+5x=-9
练习
解下列方程
答案:
(1)
(2)
(3)
(4)
(1) ? ? ? ? ? ? ? ?(2) ? ? ? ?;? (3) ? ? ? ? ? ? ? ? ; (4)
练习
解下列方程
答案:(1)y=-12;(2)x=16
(1)
(2)
练习
解下列方程
答案:
(1) x=-1 ;?(2) x=-8 ;?(3) x=-6 ;
解方程:
练习
答案:
练习
解方程:
答案:
一起来找茬
下面方程的解法对吗?如果不对,应怎样改正?
解方程:
移项,得
合并同类项,得
系数化为1,得
总结:移项一定要变号
练习
下面的移项对不对?如果不对,请改正?
(1)从5+2x=10,? ?得2x=10+5
(2)从3x=2x-5,? ? 得3x+2x=5
(3)从-2x+5=1-3x,? ? 得-2x+3x=1+5
练习
找出题中的错误,重新解方程。
......
......
......
①
②
③
例题
有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学?
解法一:设船有x条,则 ?
? ? ? ? ? ? ? ? 6(x+1)=9(x-1) ??
? ? ? ? ? ? ? ? 得出 x=5 ?
? ? ? ? ? ? ? ? 6× (5+1)=36(人) ?
答:这个班共有36人.
有一个班的同学去划船,他们算了一下,如果增加一条船,正好每条船坐6人,如果减少一条船 ,正每条船坐9人,问:这个班共多少同学?
解法二:设这个班共有同学x人,则
得出 x=36
答:这个班共有36人.
例题
例题
例4 某制药厂制造一批药品,如用旧工艺,则废水排量要比环保限制的最大量还多200 t;如用新工艺,则废水排量比环保限制的最大量少100 t. 新旧工艺的废水排量之比为2:5,两种工艺的废水排量各是多少?
答案:新工艺的废水排量是200t,?
? ? ? ? ? ?旧工艺的废水排量是500t.
练习
某学校组织学生共同种一批树,如果每人种5棵,则剩下3棵;如果每人种6棵,则缺3棵树苗,求参与种树的人数.
答案:参与种树的人数是6.
练习
天平的左边放2枚硬币和13克砝码,右边放6枚硬币和5克砝码,此时天平恰好平衡.每枚硬币的质量是多少克?
答案:每枚硬币的质量是2克.
练习
已知 2x+1 与 -12x+5 的值是相反数,求 x 的值.
答案:
练习
答案:
练习
1、解下列方程:
答案:(1)x=1;(2)x=-24
练习
2、王芳和李丽同时采摘樱桃,王芳平均每小时采摘8kg,李丽平均每小时采摘7kg.采摘结束王芳从她采摘的樱桃中取出0.25kg给了李丽,这时两人的樱桃一样多.她们采摘用了多少时间?
答案:她们采摘用了0.5小时.
总结
这节课我们学会了什么?
如何解形如?ax+b=cx+d?形式的方程
3x?+20=4x-25
移项要变号
3x?-4x?=-25-20
-x?=-45
x=45
合并同类项
系数化为1
目标:化为x=a的形式
移项
等式性质1
等式性质2
什么是移项?
移项要注意什么?
如何利用合并同类项和移项解一元一次方程?
合并同类项与移项
复习巩固
解下列方程:
复习巩固
举例说明解方程时怎样“移项”,你知道这样做的根据吗?
复习巩固
解下列方程:
用方程解答下列问题:
(1)x的5倍与2的和等于x的3倍与4的差,求x;
(2)y与-5的积等于y与5的和,求y.
复习巩固
复习巩固
小新出生时父亲28岁,现在父亲的年龄是小新年龄的3倍,求现在小新的年龄.
复习巩固
洗衣机厂今年计划生产洗衣机25500台,其中1型、2型、3型三种洗衣机的数量比为1 : 2 : 14,计划生产这三种洗衣机各多少台?
复习巩固
用一根长60m的绳子围出一个长方形,使它的长是宽的1.5倍,长和宽各应是多少?
综合运用
随着农业技术的现代化,节水型灌溉得到逐步推广.喷灌和滴灌是比漫灌节水的灌溉方式.灌溉三块同样大的实验田,第一块用漫灌方式,第二块用喷灌方式,第三块用滴灌方式.后两种方式用水量分别是漫灌的25%和15%.
(1) 设第一块实验田用水xt,则另两块实验田的用水量各如 ? ? ? ? 何表示?
(2) 如果三块实验田共用水420t,每块实验田各用水多少吨?
综合运用
某造纸厂为节约木材,大力扩大再生纸的生产,它去年10月生产再生纸2050t,这比它前年10月再生纸产量的2倍还多150t,它前年10月生产再生纸多少吨?
综合运用
把一根长100cm的木棍锯成两段,要使其中一段长比另一段长的2倍少5cm,应该在木棍的哪个位置锯开?
综合运用
几个人共同种一批树苗,如果每人种10棵,则剩下6棵树苗未种;如果每人种12棵,则缺6棵树苗.求参与种树的人数.
拓广探索
在一张普通的月历中,相邻三行里同一列的三个日期数之和能否为30?如果能,这三个数分别是多少?
拓广探索
一个两位数的个位上的数的3倍加1是十位上的数,个位上的数与十位上的数的和等于9,这个两位数是多少?
无限循环小数化分数
设0.7=x,由0.7=0.777...可知,10x=7.777...,所10x-x=7.
如何把像0.1,0.2,...,0.9 这样的无限循环小数化为分数形式?动手试一试.
形式即 ? ? ,一般地,任何一个无限循环小数都可以写为分数形式吗?如果
可以,应该怎样写呢?
我们知道分数 ? ? ?写为小数形式即0.3,反过来,无限循环小数?0.3 写为分数
先以无限循环小数0.7为例进行讨论.
.
.
.
.
.
.
.
.
.
无限循环小数化分数
再以无限循环小数0.73为例,做进一步的讨论.
无限循环小数0.73=0.737373...,它的循环节有两位,类比上面的讨论可以想到如下的做法.
设0.73=x,由0.73=0.737373...可知100x=73.7373...,所以100x-x=73.
如何把像0.10,0.12,...,0.98这样的无限循环小数化为分数形式?动手试一试.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
无限循环小数化分数
如何把无限循环小数0.735,0.823 1化为分数形式?动手
试一试,并总结把无限循环小数化为分数形式的一般规律.
