人教版七年级上册 3.3.1 实际问题与一元一次方程 课件(共31张PPT)
文档属性
| 名称 | 人教版七年级上册 3.3.1 实际问题与一元一次方程 课件(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-18 15:23:36 | ||
图片预览








文档简介
(共31张PPT)
3.3.1
实际问题与一元一次方程
配套问题
生活中,有很多需要进行配套的问题,比如我们使用的餐桌需要和椅子进行配套,你能举出生活中一些配套的问题吗?
配套问题
例1 某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母.1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
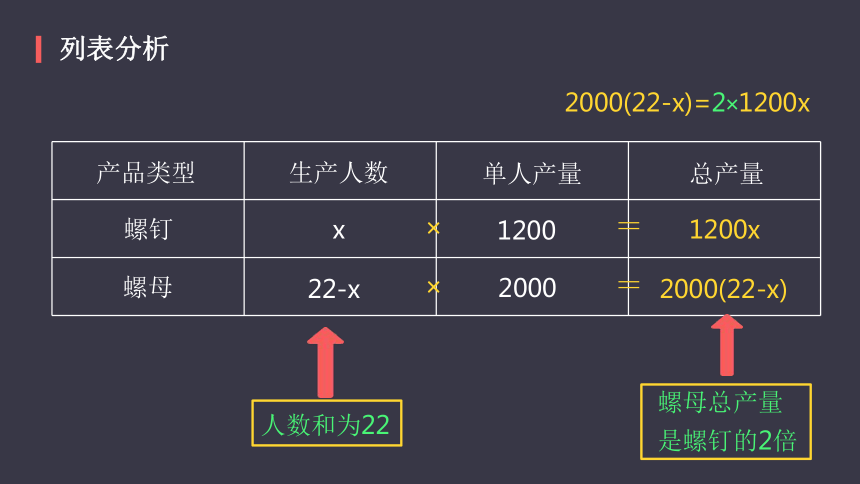
列表分析
2000(22-x)=2×1200x
产品类型
螺钉
螺母
生产人数
单人产量
总产量
x
22-x
1200x
2000(22-x)
人数和为22
螺母总产量是螺钉的2倍
1200
2000
=
=
×
×
解答过程
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得:
2
000(22-x)=2×1
200x
解方程,得:5(22-x)=6x
110-5x=6x
x=10
22-x=12
答:应安排10名工人生产螺钉,12名工人生产螺母.
检验:这显然符合实际情况
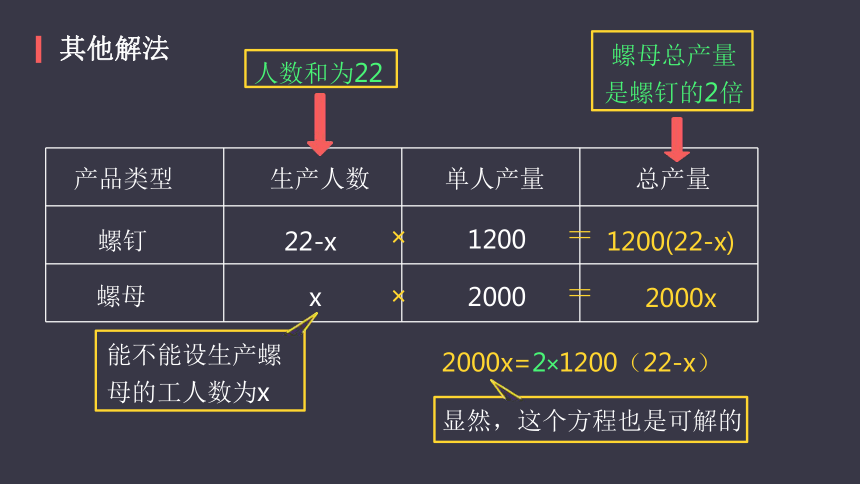
其他解法
产品类型
螺钉
螺母
生产人数
单人产量
总产量
x
22-x
2000x
1200(22-x)
人数和为22
螺母总产量是螺钉的2倍
能不能设生产螺
母的工人数为x
2000x=2×1200(22-x)
显然,这个方程也是可解的
1200
2000
=
=
×
×
练习
某车间有
24
名工人生产螺钉和螺母,每人每天可以生产
800
个螺钉或1000
个螺母,2
个螺钉要配
5
个螺母.为使每天生产的螺钉和螺母刚好配套,应该如何分配这些工人进行螺钉和螺母的生产?
答案:8人生产螺钉,16人生产螺母.
练习
某纺织厂有纺织工人300名,为增产创收,该纺织厂又增设了制衣车间,准备将这300名纺织工人合理分配到纺织车间和制衣车间.现在知道工人每人每天平均能织布30米或制4件成衣,每件成衣用布1.5米,若使生产出的布匹刚好制成成衣,问应有多少人去生产成衣?
答案:25人生产成衣.
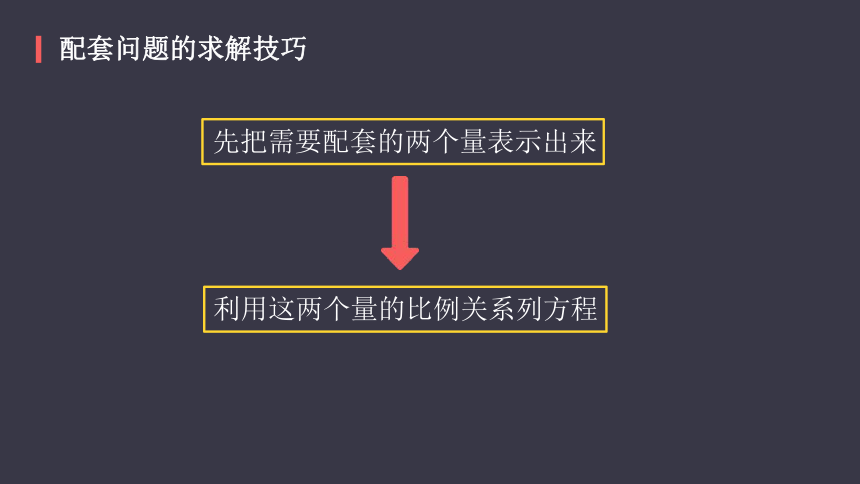
配套问题的求解技巧
先把需要配套的两个量表示出来
利用这两个量的比例关系列方程
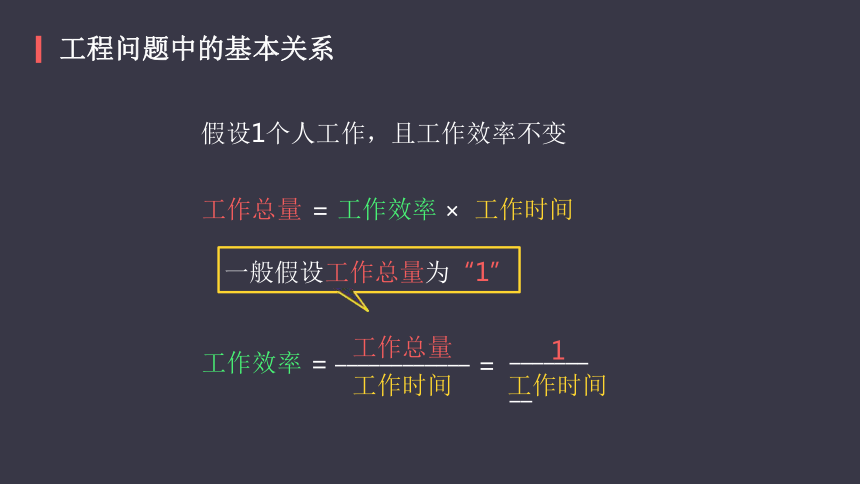
工程问题中的基本关系
假设1个人工作,且工作效率不变
工作总量
=
工作效率
×
工作时间
工作效率
=
工作总量
工作时间
工作时间
1
____________
=
_________
一般假设工作总量为“1”
工程问题中的基本关系
1、一件工作,若甲单独做
2
小时完成,那么甲单独做
1
小时完成全部工作量的_______.
2、一件工作,若甲单独做12小时完成,则甲单独做
1
小时完成全部工作量的
______,m小时完成全部工作量的_______.
工程问题
例2 整理一批图书,由一个人做要40h
完成.现计划由一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作.
假设这些人的工作效率相同,具体应该安排多少人工作?
列表分析
咋表示呢?
人均效率
人数
时间
工作量
第一阶段
第二阶段
4
8
工作量之和等
于总工作量1
x
(x+2)
+
=
1
解答过程
解:设安排
x
人先做4h,
检验:这显然
符合实际情况
依题意得:
解方程,得:4x+8(x+2)=40
4x+8x+16=40
12x=24
x=2
答:应先安排
2人做4h.
与工程有关的一元一次方程
工程问题中的基本量和基本关系是什么?
工程问题的求解技巧是什么?
练习
完成某项工程,甲单独做10天完成,乙单独做7天完成,现在由甲先做3天,乙再参加合作,求完成这项工程总共用去的时间.若设完成此项工程总共用x天,下列方程中正确(
)
D
A.
C.
B.
D.
练习
一件工作,甲单独做需50天才能完成,乙独做需要45天完成.问在乙单独做7天以后,甲、乙合作多少天可以完成?
答案:甲乙合作20天可以完成.
练习
一件工作,甲单独做20小时完成,乙单独做12小时完成,现在由甲单独做4小时,剩余的部分由甲、乙合作,需要几小时完成?
答案:需要6小时完成.
练习
某单位开展植树活动,由一个人植树要80小时完成,现由一部分人先植树5小时,由于单位有紧急事情,再增加2人,且必须在4小时之内完成植树任务,这些人的工作效率相同,应先安排多少人植树
答案:应先安排8人.
练习
某管道由甲、乙两工程队单独施工分别需要30天、20天.
答案:(1)12天;(2)两队同时施工.
(1)如果两队从两端同时相向施工,需要多少天铺好?
(2)又知甲队单独施工每天需付200元的施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施
工,还是乙队单独施工,还是两队同时施工,请你按
照少花钱多办事的原则,设计一个方案,并说明理由.
练习
一水池,单开进水管3小时可将水池注满,单开出水管4小时可将满池水放完.现对空水池先打开进水管2小时,然后打开出水管,使进水管、出水管一起开放,问再过几小时可将水池注满?
答案:再过4小时可将水池注满.
工程问题的求解技巧
设工作总量为1
把工作效率表出来
设未知数,表示出各个阶段的工作量
利用各阶段工作量之和等于1列方程
归纳
列方程解应用题大致包含哪些步骤呢?
步骤
审
设
列
解
验
答
具体含义
审题,分析题目中的数量关系
设适当的未知数,并表示未知量
根据题目中的数量关系列方程
解出这个方程
检验
作答
流程图
实际问题
设未知数,列方程
一元一次方程
实际问题
的答案
检验
一元一次方程
的解(x
=a)
解方程
练习
一套仪器由一个A部件和三个B部件构成.用1
钢材可以做40个A部件或240个B部件.
现要用6
钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
答案:应用4
钢材做A部件,2
钢材做B部件.
练习
一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天.
如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
答案:8天.
与数字有关的一元一次方程
什么是位值原理?
怎么用代数式表示一个多位数?
怎么解与数字有关的一元一次方程问题?
练习
【分析】
【解答】
【点评】
练习
【分析】
【解答】
【点评】
总结
这节课我们学会了什么?
列方程解应用题的基本步骤
步骤
审
设
列
解
验
答
具体含义
审题,分析题目中的数量关系
设适当的未知数,并表示未知量
根据题目中的数量关系列方程
解出这个方程
检验
作答
列方程解应用题的流程
总结
实际问题
设未知数,列方程
一元一次方程
实际问题
的答案
检验
一元一次方程
的解(x
=a)
解方程
3.3.1
实际问题与一元一次方程
配套问题
生活中,有很多需要进行配套的问题,比如我们使用的餐桌需要和椅子进行配套,你能举出生活中一些配套的问题吗?
配套问题
例1 某车间有22名工人,每人每天可以生产1200个螺钉或2000个螺母.1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
列表分析
2000(22-x)=2×1200x
产品类型
螺钉
螺母
生产人数
单人产量
总产量
x
22-x
1200x
2000(22-x)
人数和为22
螺母总产量是螺钉的2倍
1200
2000
=
=
×
×
解答过程
解:设应安排x名工人生产螺钉,(22-x)名工人生产螺母.
依题意得:
2
000(22-x)=2×1
200x
解方程,得:5(22-x)=6x
110-5x=6x
x=10
22-x=12
答:应安排10名工人生产螺钉,12名工人生产螺母.
检验:这显然符合实际情况
其他解法
产品类型
螺钉
螺母
生产人数
单人产量
总产量
x
22-x
2000x
1200(22-x)
人数和为22
螺母总产量是螺钉的2倍
能不能设生产螺
母的工人数为x
2000x=2×1200(22-x)
显然,这个方程也是可解的
1200
2000
=
=
×
×
练习
某车间有
24
名工人生产螺钉和螺母,每人每天可以生产
800
个螺钉或1000
个螺母,2
个螺钉要配
5
个螺母.为使每天生产的螺钉和螺母刚好配套,应该如何分配这些工人进行螺钉和螺母的生产?
答案:8人生产螺钉,16人生产螺母.
练习
某纺织厂有纺织工人300名,为增产创收,该纺织厂又增设了制衣车间,准备将这300名纺织工人合理分配到纺织车间和制衣车间.现在知道工人每人每天平均能织布30米或制4件成衣,每件成衣用布1.5米,若使生产出的布匹刚好制成成衣,问应有多少人去生产成衣?
答案:25人生产成衣.
配套问题的求解技巧
先把需要配套的两个量表示出来
利用这两个量的比例关系列方程
工程问题中的基本关系
假设1个人工作,且工作效率不变
工作总量
=
工作效率
×
工作时间
工作效率
=
工作总量
工作时间
工作时间
1
____________
=
_________
一般假设工作总量为“1”
工程问题中的基本关系
1、一件工作,若甲单独做
2
小时完成,那么甲单独做
1
小时完成全部工作量的_______.
2、一件工作,若甲单独做12小时完成,则甲单独做
1
小时完成全部工作量的
______,m小时完成全部工作量的_______.
工程问题
例2 整理一批图书,由一个人做要40h
完成.现计划由一部分人先做4h,然后增加2人与他们一起做8h,完成这项工作.
假设这些人的工作效率相同,具体应该安排多少人工作?
列表分析
咋表示呢?
人均效率
人数
时间
工作量
第一阶段
第二阶段
4
8
工作量之和等
于总工作量1
x
(x+2)
+
=
1
解答过程
解:设安排
x
人先做4h,
检验:这显然
符合实际情况
依题意得:
解方程,得:4x+8(x+2)=40
4x+8x+16=40
12x=24
x=2
答:应先安排
2人做4h.
与工程有关的一元一次方程
工程问题中的基本量和基本关系是什么?
工程问题的求解技巧是什么?
练习
完成某项工程,甲单独做10天完成,乙单独做7天完成,现在由甲先做3天,乙再参加合作,求完成这项工程总共用去的时间.若设完成此项工程总共用x天,下列方程中正确(
)
D
A.
C.
B.
D.
练习
一件工作,甲单独做需50天才能完成,乙独做需要45天完成.问在乙单独做7天以后,甲、乙合作多少天可以完成?
答案:甲乙合作20天可以完成.
练习
一件工作,甲单独做20小时完成,乙单独做12小时完成,现在由甲单独做4小时,剩余的部分由甲、乙合作,需要几小时完成?
答案:需要6小时完成.
练习
某单位开展植树活动,由一个人植树要80小时完成,现由一部分人先植树5小时,由于单位有紧急事情,再增加2人,且必须在4小时之内完成植树任务,这些人的工作效率相同,应先安排多少人植树
答案:应先安排8人.
练习
某管道由甲、乙两工程队单独施工分别需要30天、20天.
答案:(1)12天;(2)两队同时施工.
(1)如果两队从两端同时相向施工,需要多少天铺好?
(2)又知甲队单独施工每天需付200元的施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施
工,还是乙队单独施工,还是两队同时施工,请你按
照少花钱多办事的原则,设计一个方案,并说明理由.
练习
一水池,单开进水管3小时可将水池注满,单开出水管4小时可将满池水放完.现对空水池先打开进水管2小时,然后打开出水管,使进水管、出水管一起开放,问再过几小时可将水池注满?
答案:再过4小时可将水池注满.
工程问题的求解技巧
设工作总量为1
把工作效率表出来
设未知数,表示出各个阶段的工作量
利用各阶段工作量之和等于1列方程
归纳
列方程解应用题大致包含哪些步骤呢?
步骤
审
设
列
解
验
答
具体含义
审题,分析题目中的数量关系
设适当的未知数,并表示未知量
根据题目中的数量关系列方程
解出这个方程
检验
作答
流程图
实际问题
设未知数,列方程
一元一次方程
实际问题
的答案
检验
一元一次方程
的解(x
=a)
解方程
练习
一套仪器由一个A部件和三个B部件构成.用1
钢材可以做40个A部件或240个B部件.
现要用6
钢材制作这种仪器,应用多少钢材做A部件,多少钢材做B部件,恰好配成这种仪器多少套?
答案:应用4
钢材做A部件,2
钢材做B部件.
练习
一条地下管线由甲工程队单独铺设需要12天,由乙工程队单独铺设需要24天.
如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
答案:8天.
与数字有关的一元一次方程
什么是位值原理?
怎么用代数式表示一个多位数?
怎么解与数字有关的一元一次方程问题?
练习
【分析】
【解答】
【点评】
练习
【分析】
【解答】
【点评】
总结
这节课我们学会了什么?
列方程解应用题的基本步骤
步骤
审
设
列
解
验
答
具体含义
审题,分析题目中的数量关系
设适当的未知数,并表示未知量
根据题目中的数量关系列方程
解出这个方程
检验
作答
列方程解应用题的流程
总结
实际问题
设未知数,列方程
一元一次方程
实际问题
的答案
检验
一元一次方程
的解(x
=a)
解方程
