北师大版数学必修4同步教学课:第1章-4.1+4.2 单位圆与任意角的正弦函数、余弦函数的定义 单位圆与周期性
文档属性
| 名称 | 北师大版数学必修4同步教学课:第1章-4.1+4.2 单位圆与任意角的正弦函数、余弦函数的定义 单位圆与周期性 |

|
|
| 格式 | zip | ||
| 文件大小 | 457.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-03 00:00:00 | ||
图片预览










文档简介
课件31张PPT。§4 正弦函数和余弦函数的定义与诱导公式
4.1 单位圆与任意角的正弦函数、余弦函数的定义
4.2 单位圆与周期性内容要求 1.了解单位圆与正弦、余弦函数的关系.2.掌握任意角的正弦、余弦的定义(重点).3.掌握正弦函数、余弦函数在各个象限内的符号(重点).4.了解周期函数的概念,理解正弦函数、余弦函数都是周期函数(难点).
知识点1 任意角的正弦、余弦函数
(1)单位圆
在直角坐标系中,以 为圆心,以 为半径的圆,称为单位圆.原点 单位长度 (2)正弦函数、余弦函数的定义
如图,在直角坐标系中,给定单位圆,对于任意角α,使角α的顶点与原点重合,始边与x轴正半轴重合,终边与单位圆交于点P(u,v),那么点P的 叫作角α的正弦函数,记作 ;点P的 叫作角α的余弦函数,记作 .纵坐标v v=sin α 横坐标u u=cosα (3)正弦函数、余弦函数的定义域和值域
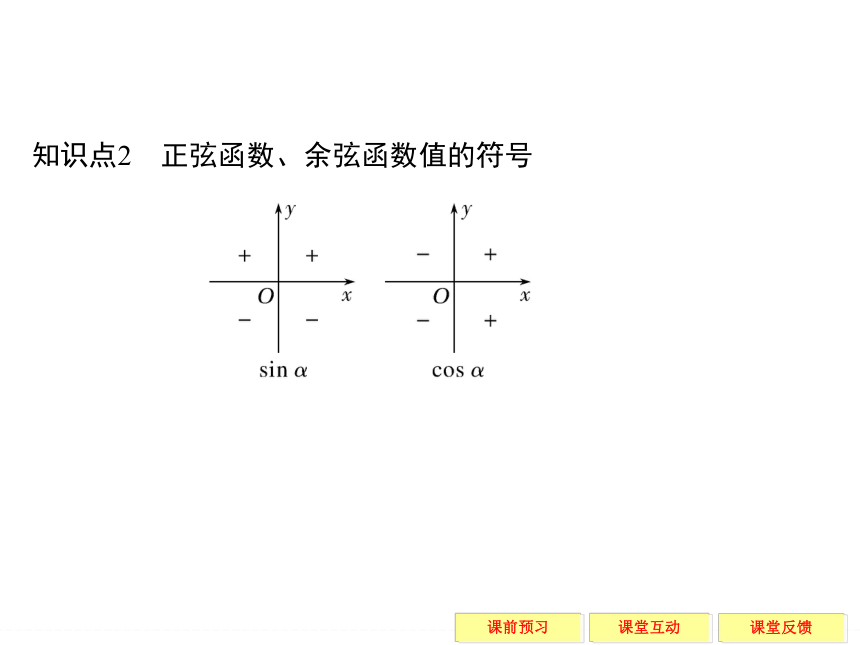
正弦函数y=sin x和余弦函数y=cos x的定义域为 ,值域为 .全体实数 [-1,1] 答案 B知识点2 正弦函数、余弦函数值的符号【预习评价】
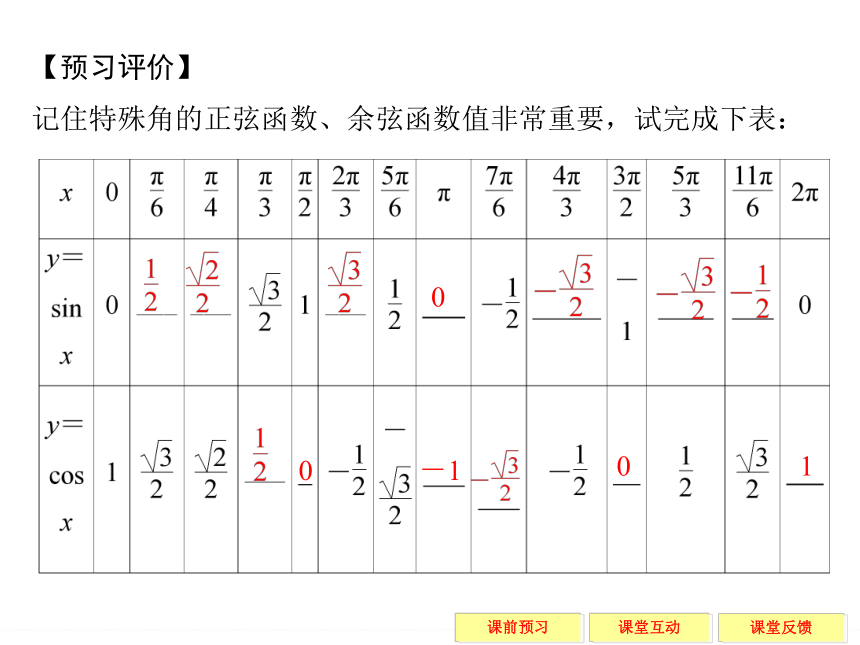
记住特殊角的正弦函数、余弦函数值非常重要,试完成下表:0 0 -1 0 1 知识点3 周期函数
(1)一般地,对于函数f(x),如果存在非零实数T,对定义域内的任意一个x值, 都成立.那么就把函数f(x)称为周期函数,T叫作这个函数的 .
(2)y=sin x的周期为 ,最小正周期为 .
y=cos x的周期为 ,最小正周期为 .f(x+T)=f(x) 周期 2kπ,k∈Z 2π 2kπ,k∈Z 2π 【预习评价】
如果存在非零常数T,对于函数f(x),若存在x值有f(x+T)=f(x),则函数f(x)是周期函数吗?
提示 不一定,如函数f(x)=x2,存在非零常数T=4,存在x=-2,使得f(-2+4)=f(-2),但是函数f(x)=x2不是周期函数. 答案 -8规律方法 利用正弦函数、余弦函数的定义,求一个角的正弦函数、余弦函数,需要确定三个量:角的终边上任意一个异于原点的点P的横坐标x、纵坐标y和点P到原点的距离r.特别注意,当点的坐标含有参数时,应分类讨论.【训练1】 若点P(2m,-3m)(m<0)在角α的终边上,则sin α=________.题型二 有关三角函数值的符号问题
【例2】 (1)α是第二象限角,判断sin αcos α的正负;
(2)若sin αcos α<0,判断α是第几象限角.规律方法 正余弦函数符号的确定
(1)终边在坐标轴上的角:
终边在坐标轴上的角可以利用单位圆,如终边在x轴非正半轴上的角与单位圆的交点为(-1,0),故sin α=0,cos α=-1.
(2)终边在各个象限内的角:
利用定义记符号:正弦取决于终边上点的纵坐标,所以一、二象限为正;余弦取决于终边上点的横坐标,所以一、四象限为正. 解 ∵f(x)是奇函数,
∴f(-x)=-f(x),
又∵f(x+π)=f(x),
∴函数f(x)的周期为π, 答案 2π答案 A 答案 A 答案 1课堂小结
1.利用定义求α的正弦函数值与余弦函数值时,注意结合图形求出α的终边与单位圆的交点坐标,即得值.
2.正弦、余弦函数值在各个象限的符号可简记为:一均正、二正弦、三均负、四余弦.
3.正弦、余弦函数的周期性反映了终边相同的角的同一三角函数值相等.作用是把求任意角的三角函数值转化为求0~2π(或0°~360°)范围内角的三角函数值.
4.1 单位圆与任意角的正弦函数、余弦函数的定义
4.2 单位圆与周期性内容要求 1.了解单位圆与正弦、余弦函数的关系.2.掌握任意角的正弦、余弦的定义(重点).3.掌握正弦函数、余弦函数在各个象限内的符号(重点).4.了解周期函数的概念,理解正弦函数、余弦函数都是周期函数(难点).
知识点1 任意角的正弦、余弦函数
(1)单位圆
在直角坐标系中,以 为圆心,以 为半径的圆,称为单位圆.原点 单位长度 (2)正弦函数、余弦函数的定义
如图,在直角坐标系中,给定单位圆,对于任意角α,使角α的顶点与原点重合,始边与x轴正半轴重合,终边与单位圆交于点P(u,v),那么点P的 叫作角α的正弦函数,记作 ;点P的 叫作角α的余弦函数,记作 .纵坐标v v=sin α 横坐标u u=cosα (3)正弦函数、余弦函数的定义域和值域
正弦函数y=sin x和余弦函数y=cos x的定义域为 ,值域为 .全体实数 [-1,1] 答案 B知识点2 正弦函数、余弦函数值的符号【预习评价】
记住特殊角的正弦函数、余弦函数值非常重要,试完成下表:0 0 -1 0 1 知识点3 周期函数
(1)一般地,对于函数f(x),如果存在非零实数T,对定义域内的任意一个x值, 都成立.那么就把函数f(x)称为周期函数,T叫作这个函数的 .
(2)y=sin x的周期为 ,最小正周期为 .
y=cos x的周期为 ,最小正周期为 .f(x+T)=f(x) 周期 2kπ,k∈Z 2π 2kπ,k∈Z 2π 【预习评价】
如果存在非零常数T,对于函数f(x),若存在x值有f(x+T)=f(x),则函数f(x)是周期函数吗?
提示 不一定,如函数f(x)=x2,存在非零常数T=4,存在x=-2,使得f(-2+4)=f(-2),但是函数f(x)=x2不是周期函数. 答案 -8规律方法 利用正弦函数、余弦函数的定义,求一个角的正弦函数、余弦函数,需要确定三个量:角的终边上任意一个异于原点的点P的横坐标x、纵坐标y和点P到原点的距离r.特别注意,当点的坐标含有参数时,应分类讨论.【训练1】 若点P(2m,-3m)(m<0)在角α的终边上,则sin α=________.题型二 有关三角函数值的符号问题
【例2】 (1)α是第二象限角,判断sin αcos α的正负;
(2)若sin αcos α<0,判断α是第几象限角.规律方法 正余弦函数符号的确定
(1)终边在坐标轴上的角:
终边在坐标轴上的角可以利用单位圆,如终边在x轴非正半轴上的角与单位圆的交点为(-1,0),故sin α=0,cos α=-1.
(2)终边在各个象限内的角:
利用定义记符号:正弦取决于终边上点的纵坐标,所以一、二象限为正;余弦取决于终边上点的横坐标,所以一、四象限为正. 解 ∵f(x)是奇函数,
∴f(-x)=-f(x),
又∵f(x+π)=f(x),
∴函数f(x)的周期为π, 答案 2π答案 A 答案 A 答案 1课堂小结
1.利用定义求α的正弦函数值与余弦函数值时,注意结合图形求出α的终边与单位圆的交点坐标,即得值.
2.正弦、余弦函数值在各个象限的符号可简记为:一均正、二正弦、三均负、四余弦.
3.正弦、余弦函数的周期性反映了终边相同的角的同一三角函数值相等.作用是把求任意角的三角函数值转化为求0~2π(或0°~360°)范围内角的三角函数值.
