北师大版数学必修4同步教学课:第1章-5.2 正弦函数的图像
文档属性
| 名称 | 北师大版数学必修4同步教学课:第1章-5.2 正弦函数的图像 |

|
|
| 格式 | zip | ||
| 文件大小 | 512.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-03 00:00:00 | ||
图片预览








文档简介
课件27张PPT。§5 正弦函数的图像与性质
5.2 正弦函数的图像
内容要求 1.能用“五点法”画正弦函数在[0,2π]上的图像(重点).2.理解正弦曲线的意义(难点).知识点1 正弦线
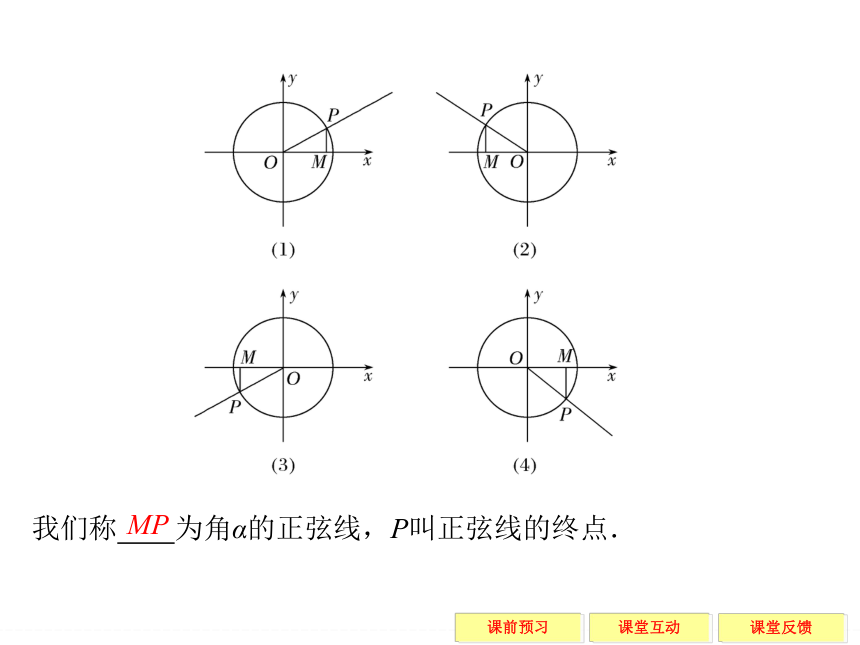
如图所示,设任意角α的顶点在原点O,始边与x轴的非负半轴重合,终边与单位圆O相交于点P(x,y),过P点作x轴的垂线,垂足为M.我们称 为角α的正弦线,P叫正弦线的终点.MP 【预习评价】
(正确的打“√”,错误的打“×”)
(1)在正弦线的定义中MP也可以写成PM的形式.( )
(2)正弦线是一条有方向的有向线段.( )× √ 知识点2 正弦函数图像的画法
(1)几何法
利用几何法作正弦函数y=sin x,x∈[0,2π]的图像的过程如下:
①作直角坐标系,并在直角坐标系y轴的左侧画单位圆,如图所示.(2)“五点法”
在函数y=sin x,x∈[0,2π]的图像上,起关键作用的点有以下五个: , , , , .事实上,找出这五个点后,函数y=sin x,x∈[0,2π]的图像形状就基本上确定了.因此,在精确度要求不太高时,我们常常先找出这五个关键点,再用光滑的曲线顺次将它们连接起来,就可以得到函数的简图.这种方法称为“ ”.(0,0) (π,0) (2π,0) 五点法 【预习评价】
1.函数y=sin x在[0,2π]上的单调减区间为________,最大值为________.
2.利用五点法作函数y=Asin x(A>0)的图像时,选取的五个关键点是什么?题型一 “五点法”作函数的图像
【例1】 利用“五点法”作出y=-1+sin x (x∈[0,2π])的简图.解 按五个关键点列表:
描点并将它们用光滑的曲线连接起来(如图所示).规律方法 “五点法”作图的实质是选取函数的一个周期,将其四等分,分别找出图像的最高点、最低点及图像与x轴的交点等五个关键点,由这五个点大致确定图像的位置和形状.【训练1】 (1)作出函数y=2sin x(0≤x≤2π)的图像.
(2)用“五点法”画出函数y=sin 2x(0≤x≤π)的图像.
答案 A(2)求方程lg x=sin x的实数解的个数.
解 作出y=lg x,y=sin x在同一坐标系内的图像,则方程根的个数即为两函数图像交点的个数,由图像知方程有三个实根.方向3 求参数的取值范围
【例2-3】 函数f(x)=sin x+2|sin x|,x∈[0,2π]的图像与直线y=k有且仅有两个不同的交点,求实数k的取值范围.规律方法 1.三角函数的图像是研究函数的重要工具,通过图像可较简便地解决问题,这正是数形结合思想方法的应用.
2.一般地,函数y=|f(x)|的图像可将函数y=f(x)的图像作如下变换得到:在x轴下方的图像以x轴为对称轴翻折到x轴上方,x轴上方的部分保持不变. 答案 D 答案 A 解析 画出y=sin x的图像(图像略)可得. 答案 3π5.在[0,2π]内,用五点法作出函数y=2sin x-1的图像.
5.2 正弦函数的图像
内容要求 1.能用“五点法”画正弦函数在[0,2π]上的图像(重点).2.理解正弦曲线的意义(难点).知识点1 正弦线
如图所示,设任意角α的顶点在原点O,始边与x轴的非负半轴重合,终边与单位圆O相交于点P(x,y),过P点作x轴的垂线,垂足为M.我们称 为角α的正弦线,P叫正弦线的终点.MP 【预习评价】
(正确的打“√”,错误的打“×”)
(1)在正弦线的定义中MP也可以写成PM的形式.( )
(2)正弦线是一条有方向的有向线段.( )× √ 知识点2 正弦函数图像的画法
(1)几何法
利用几何法作正弦函数y=sin x,x∈[0,2π]的图像的过程如下:
①作直角坐标系,并在直角坐标系y轴的左侧画单位圆,如图所示.(2)“五点法”
在函数y=sin x,x∈[0,2π]的图像上,起关键作用的点有以下五个: , , , , .事实上,找出这五个点后,函数y=sin x,x∈[0,2π]的图像形状就基本上确定了.因此,在精确度要求不太高时,我们常常先找出这五个关键点,再用光滑的曲线顺次将它们连接起来,就可以得到函数的简图.这种方法称为“ ”.(0,0) (π,0) (2π,0) 五点法 【预习评价】
1.函数y=sin x在[0,2π]上的单调减区间为________,最大值为________.
2.利用五点法作函数y=Asin x(A>0)的图像时,选取的五个关键点是什么?题型一 “五点法”作函数的图像
【例1】 利用“五点法”作出y=-1+sin x (x∈[0,2π])的简图.解 按五个关键点列表:
描点并将它们用光滑的曲线连接起来(如图所示).规律方法 “五点法”作图的实质是选取函数的一个周期,将其四等分,分别找出图像的最高点、最低点及图像与x轴的交点等五个关键点,由这五个点大致确定图像的位置和形状.【训练1】 (1)作出函数y=2sin x(0≤x≤2π)的图像.
(2)用“五点法”画出函数y=sin 2x(0≤x≤π)的图像.
答案 A(2)求方程lg x=sin x的实数解的个数.
解 作出y=lg x,y=sin x在同一坐标系内的图像,则方程根的个数即为两函数图像交点的个数,由图像知方程有三个实根.方向3 求参数的取值范围
【例2-3】 函数f(x)=sin x+2|sin x|,x∈[0,2π]的图像与直线y=k有且仅有两个不同的交点,求实数k的取值范围.规律方法 1.三角函数的图像是研究函数的重要工具,通过图像可较简便地解决问题,这正是数形结合思想方法的应用.
2.一般地,函数y=|f(x)|的图像可将函数y=f(x)的图像作如下变换得到:在x轴下方的图像以x轴为对称轴翻折到x轴上方,x轴上方的部分保持不变. 答案 D 答案 A 解析 画出y=sin x的图像(图像略)可得. 答案 3π5.在[0,2π]内,用五点法作出函数y=2sin x-1的图像.
