北师大版数学必修4同步教学课:第1章-7.1+7.2 正切函数的定义 正切函数的图像与性质
文档属性
| 名称 | 北师大版数学必修4同步教学课:第1章-7.1+7.2 正切函数的定义 正切函数的图像与性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 674.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-03 00:00:00 | ||
图片预览











文档简介
课件35张PPT。§7 正切函数
7.1 正切函数的定义
7.2 正切函数的图像与性质
内容要求 1.能借助单位圆中的正切线画出函数y=tan x的图像.2.掌握正切函数的图像、定义域、值域、单调性、奇偶性、周期性等性质(重点).3.注重数形结合思想的应用以及正切函数与正、余弦函数的综合应用(难点).tan α(2)正切函数与正弦、余弦函数的关系:
根据定义知tan α= (α∈R,α≠kπ+,k∈Z).
(3)正切值在各象限的符号:
根据定义知,当角在第 和第 象限时,其正切函数值为正;当角在第 和第 象限时,其正切函数值为负.
(4)正切线:
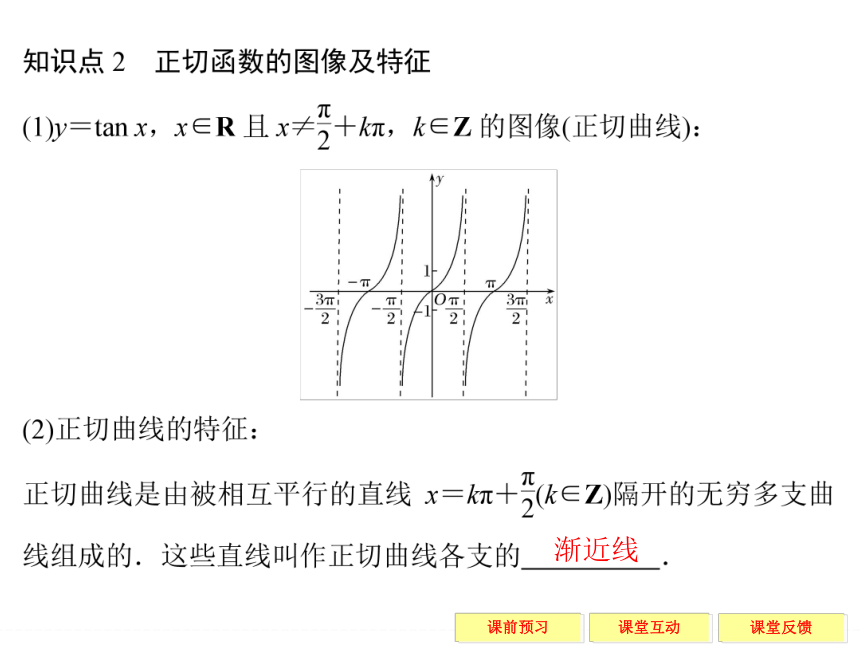
在单位圆中令A(1,0),过A作x轴的垂线,与角α的终边或终边的延长线相交于T,称线段 为角α的正切线.一 三 二 四 AT 答案 B2.函数y=tan 2x的定义域为________.渐近线 【预习评价】
正切函数是奇函数,图像关于原点对称,那么正切函数的对称中心只有一个吗?
提示 正切函数的对称中心除了原点外,诸如(π,0)等都是对称中心,正切函数有无数个对称中心.知识点3 正切函数的性质R kπ(k∈Z,k≠0) π 奇函数 【预习评价】 (正确的打“√”,错误的打“×”)
(1)正切函数为定义域上的增函数( )
(2)正切函数存在闭区间[a,b],使y=tan x是增加的.( )
(3)若x是第一象限的角,则y=tan x是增函数( )
(4)正切函数y=tan x的对称中心为(kπ,0)k∈Z.( )× √ × × 题型一 正切函数的定义
【例1】 已知角α的终边经过点P(-4a,3a)(a≠0),求sin α,cos α、tan α的值.(2)根据正切函数的图像,写出tan x≥-1的解集.方向1 比较大小
【例3-1】 比较tan 1、tan 2、tan 3的大小.规律方法 1.比较同名三角函数值的大小,实质上是将两个角利用周期性放在同一个单调区间内,利用单调性比较大小.
2.对于形如y=tan(ωx+φ)(ω、φ为非零常数)的函数性质和图像的研究,应以正切函数的性质与图像为基础,运用整体思想和换元法求解.如果ω<0,一般先利用诱导公式将x的系数化为正数,再进行求解. 答案 C答案 C3.已知点P(tan α,cos α)在第二象限,则α的终边在第________象限.
解析 由P点在第二象限.∴tan α<0,cos α>0,
∴α在第四象限.
答案 四
7.1 正切函数的定义
7.2 正切函数的图像与性质
内容要求 1.能借助单位圆中的正切线画出函数y=tan x的图像.2.掌握正切函数的图像、定义域、值域、单调性、奇偶性、周期性等性质(重点).3.注重数形结合思想的应用以及正切函数与正、余弦函数的综合应用(难点).tan α(2)正切函数与正弦、余弦函数的关系:
根据定义知tan α= (α∈R,α≠kπ+,k∈Z).
(3)正切值在各象限的符号:
根据定义知,当角在第 和第 象限时,其正切函数值为正;当角在第 和第 象限时,其正切函数值为负.
(4)正切线:
在单位圆中令A(1,0),过A作x轴的垂线,与角α的终边或终边的延长线相交于T,称线段 为角α的正切线.一 三 二 四 AT 答案 B2.函数y=tan 2x的定义域为________.渐近线 【预习评价】
正切函数是奇函数,图像关于原点对称,那么正切函数的对称中心只有一个吗?
提示 正切函数的对称中心除了原点外,诸如(π,0)等都是对称中心,正切函数有无数个对称中心.知识点3 正切函数的性质R kπ(k∈Z,k≠0) π 奇函数 【预习评价】 (正确的打“√”,错误的打“×”)
(1)正切函数为定义域上的增函数( )
(2)正切函数存在闭区间[a,b],使y=tan x是增加的.( )
(3)若x是第一象限的角,则y=tan x是增函数( )
(4)正切函数y=tan x的对称中心为(kπ,0)k∈Z.( )× √ × × 题型一 正切函数的定义
【例1】 已知角α的终边经过点P(-4a,3a)(a≠0),求sin α,cos α、tan α的值.(2)根据正切函数的图像,写出tan x≥-1的解集.方向1 比较大小
【例3-1】 比较tan 1、tan 2、tan 3的大小.规律方法 1.比较同名三角函数值的大小,实质上是将两个角利用周期性放在同一个单调区间内,利用单调性比较大小.
2.对于形如y=tan(ωx+φ)(ω、φ为非零常数)的函数性质和图像的研究,应以正切函数的性质与图像为基础,运用整体思想和换元法求解.如果ω<0,一般先利用诱导公式将x的系数化为正数,再进行求解. 答案 C答案 C3.已知点P(tan α,cos α)在第二象限,则α的终边在第________象限.
解析 由P点在第二象限.∴tan α<0,cos α>0,
∴α在第四象限.
答案 四
