北师大版数学必修4同步教学课:第1章-三角函数章末复习课
文档属性
| 名称 | 北师大版数学必修4同步教学课:第1章-三角函数章末复习课 |  | |
| 格式 | zip | ||
| 文件大小 | 754.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-03 22:50:00 | ||
图片预览









文档简介
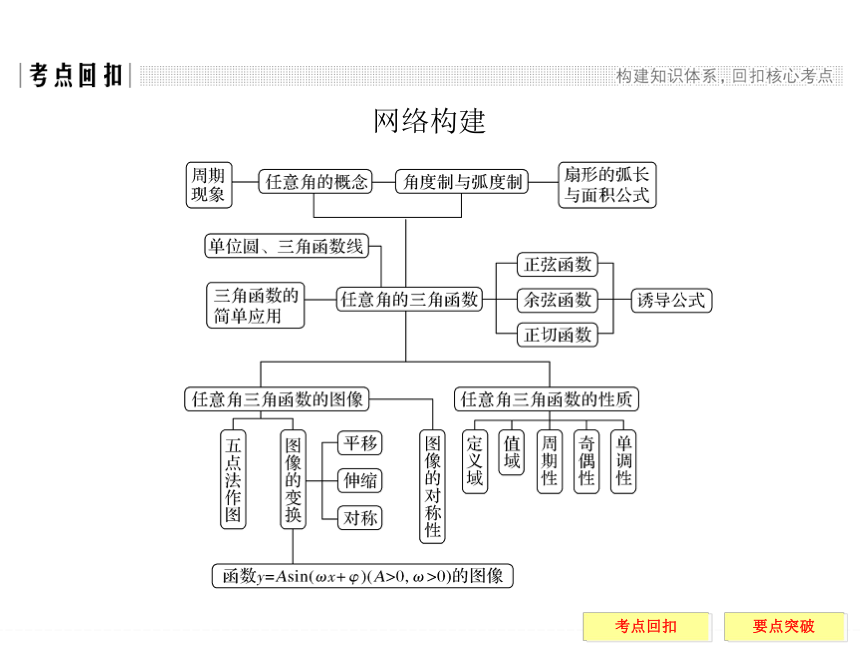
课件38张PPT。章末复习课网络构建核心归纳
1.三角函数的概念:重点掌握以下两方面内容:(1)理解任意角的概念和弧度的意义,能正确迅速地进行弧度与角度的换算.(2)掌握任意的角α的正弦、余弦和正切的定义,能正确快速利用三角函数值在各个象限的符号解题,能求三角函数的定义域和一些简单三角函数的值域.2.诱导公式:能用诱导公式将任意角的三角函数化为锐角三角函数,利用“奇变偶不变,符号看象限”牢记所有诱导公式.
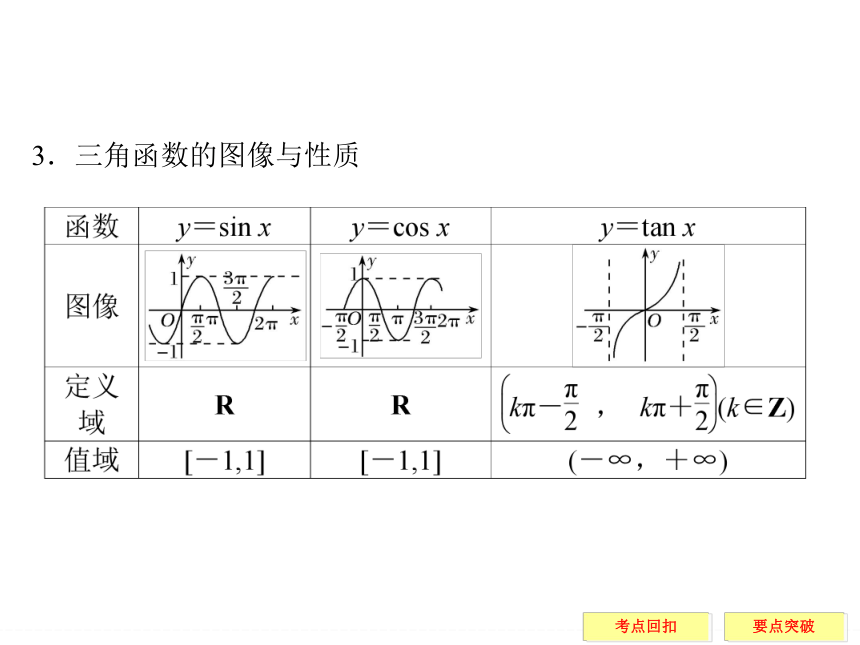
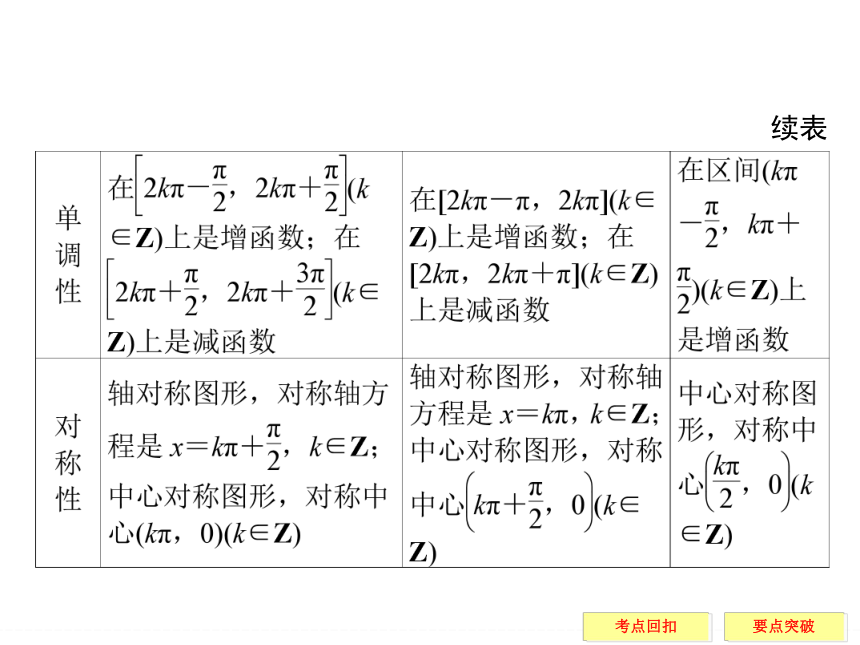
善于将同角三角函数的基本关系式和诱导公式结合起来使用,通过这些公式进行化简、求值,达到培养推理运算能力和逻辑思维能力提高的目的.3.三角函数的图像与性质续表续表4.三角函数的图像与性质的应用
(1)重点掌握“五点法”,会进行三角函数图像的变换,能从图像中获取尽可能多的信息,如周期、半个周期、四分之一个周期等,如轴对称、中心对称等,如最高点、最低点与对称中心之间位置关系等.能从三角函数的图像归纳出函数的性质.
(2)牢固掌握三角函数的定义域、值域、周期性、单调性、奇偶性和对称性.在运用三角函数性质解题时,要善于运用数形结合思想、分类讨论思想、化归转化思想将综合性较强的试题完整准确地进行解答.要点一 任意角的三角函数的定义
有关三角函数的概念主要有以下两个方面:
(1)任意角和弧度制,理解任意角的概念,弧度制的意义,能正确地进行弧度与角度的换算.
(2)任意角的三角函数,掌握任意角的正弦、余弦、正切的定义及三角函数线,能够利用三角函数线判断三角函数的符号,借助三角函数线求三角函数的定义域.【例1】 已知cos θ=m,|m|≤1,求sin θ,tan θ的值.答案 (1)A (2)1 答案 C 【例4】 f(x)是定义在R上的偶函数,对任意实数x满足f(x+2)=f(x),且f(x)在[-3,-2]上单调递减,而α,β是锐角三角形的两个内角,求证:f(sin α)>f(cos β).
证明 ∵f(x+2)=f(x),
∴y=f(x)的周期为2.
∴f(x)在[-1,0]与[-3,-2]上的单调性相同.
∴f(x)在[-1,0]上单调递减.
∵f(x)是偶函数,
∴f(x)在[0,1]上的单调性与[-1,0]上的单调性相反.
∴f(x)在[0,1]上单调递增.①要点五 三角函数的综合应用
(1)求解复合函数的有关性质问题时,应同时考虑到内层函数与外层函数的各自特征及它们的相互制约关系,准确地进行等价转化;
(2)在求三角函数的定义域时,不仅要考虑函数式有意义,而且要注意三角函数各自的定义域的要求.一般是归结为解三角函数不等式(组),可用图像法或单位圆法;
(3)求复合函数的单调区间应按照复合函数单调性的规则进行;
(4)用周期函数的定义求函数的周期是求周期的根本方法,在证明有关函数的周期性问题时,也常用周期函数的定义来处理.【训练5】 函数f(x)=cos x+2|cos x|在[0,2π]上与直线y=m有 且仅有2个交点,求m的取值范围.
1.三角函数的概念:重点掌握以下两方面内容:(1)理解任意角的概念和弧度的意义,能正确迅速地进行弧度与角度的换算.(2)掌握任意的角α的正弦、余弦和正切的定义,能正确快速利用三角函数值在各个象限的符号解题,能求三角函数的定义域和一些简单三角函数的值域.2.诱导公式:能用诱导公式将任意角的三角函数化为锐角三角函数,利用“奇变偶不变,符号看象限”牢记所有诱导公式.
善于将同角三角函数的基本关系式和诱导公式结合起来使用,通过这些公式进行化简、求值,达到培养推理运算能力和逻辑思维能力提高的目的.3.三角函数的图像与性质续表续表4.三角函数的图像与性质的应用
(1)重点掌握“五点法”,会进行三角函数图像的变换,能从图像中获取尽可能多的信息,如周期、半个周期、四分之一个周期等,如轴对称、中心对称等,如最高点、最低点与对称中心之间位置关系等.能从三角函数的图像归纳出函数的性质.
(2)牢固掌握三角函数的定义域、值域、周期性、单调性、奇偶性和对称性.在运用三角函数性质解题时,要善于运用数形结合思想、分类讨论思想、化归转化思想将综合性较强的试题完整准确地进行解答.要点一 任意角的三角函数的定义
有关三角函数的概念主要有以下两个方面:
(1)任意角和弧度制,理解任意角的概念,弧度制的意义,能正确地进行弧度与角度的换算.
(2)任意角的三角函数,掌握任意角的正弦、余弦、正切的定义及三角函数线,能够利用三角函数线判断三角函数的符号,借助三角函数线求三角函数的定义域.【例1】 已知cos θ=m,|m|≤1,求sin θ,tan θ的值.答案 (1)A (2)1 答案 C 【例4】 f(x)是定义在R上的偶函数,对任意实数x满足f(x+2)=f(x),且f(x)在[-3,-2]上单调递减,而α,β是锐角三角形的两个内角,求证:f(sin α)>f(cos β).
证明 ∵f(x+2)=f(x),
∴y=f(x)的周期为2.
∴f(x)在[-1,0]与[-3,-2]上的单调性相同.
∴f(x)在[-1,0]上单调递减.
∵f(x)是偶函数,
∴f(x)在[0,1]上的单调性与[-1,0]上的单调性相反.
∴f(x)在[0,1]上单调递增.①要点五 三角函数的综合应用
(1)求解复合函数的有关性质问题时,应同时考虑到内层函数与外层函数的各自特征及它们的相互制约关系,准确地进行等价转化;
(2)在求三角函数的定义域时,不仅要考虑函数式有意义,而且要注意三角函数各自的定义域的要求.一般是归结为解三角函数不等式(组),可用图像法或单位圆法;
(3)求复合函数的单调区间应按照复合函数单调性的规则进行;
(4)用周期函数的定义求函数的周期是求周期的根本方法,在证明有关函数的周期性问题时,也常用周期函数的定义来处理.【训练5】 函数f(x)=cos x+2|cos x|在[0,2π]上与直线y=m有 且仅有2个交点,求m的取值范围.
