人教版七年级数学上册第三章 一元一次方程3.1.2 等式的性质 教学课件(共50张PPT)
文档属性
| 名称 | 人教版七年级数学上册第三章 一元一次方程3.1.2 等式的性质 教学课件(共50张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-04 00:00:00 | ||
图片预览











文档简介
(共50张PPT)
一元一次方程的定义:
化简后只含有一个未知数(元),并且未知数的指数是1(次)的整式方程叫一元一次方程.
注意:1、一定是化简后只含一个未知数
2、分母一定不含未知数
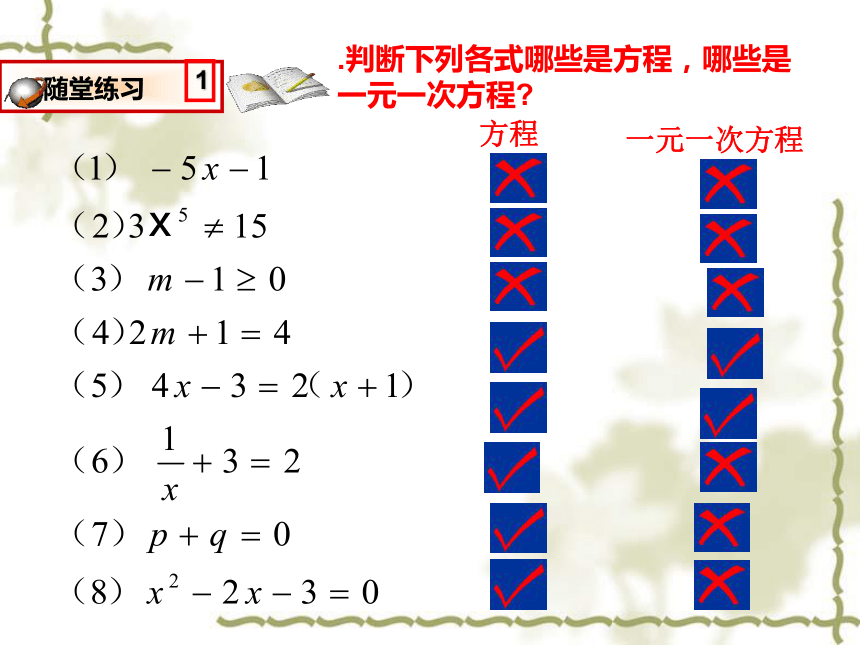
方程
一元一次方程
.判断下列各式哪些是方程,哪些是一元一次方程?
随堂练习
1
1.填空
(1)如果关于x的方程3x5-2k-3=0是一元一次方程,则k= ;
(2)已知方程 -(m-1)y|m|+3=0是一元一次方程,则m= 。
当堂测试
1
2
-1
如果x=62,
方程左边=2×62-5 =119,
右边=121,
左边≠右边
如果x=63,
方程左边=2 ×63-5=121,
右边=121,
左边=右边
使方程两边的值相等的未知数的值叫做方程的解
x = 63是方程2x-5=121的解
∴
∴
想一想:
关于x的方程 3x – 10 = mx 的解为2,
那么你知道m的值是多少吗,为什么?
3.1.2 等式的性质
判断下列各式是否为等式?
学中感知
你能用自己的方法求下列方程
的解吗?
很简单,就是
到底是什么呢?
学中感知
探究等式性质1
学中获知
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
等 式
a = b
+ +
平衡的天平
等 式
a +c = b+c
小结:平衡的天平两边都
加上同样的量,天平依然平
衡
结论:等式两边加上同一个数
(或同一个式子)结果仍相等
︴
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
等 式
a = b
结论:平衡的天平两边都减去
同样的量。天平依然平衡。
结论: 等式两边都减去同一个
数(或式子)。结果仍相等。
- -
平衡的天平
等 式
a -c = b-c
︴
等式性质1:
等式两边加(或减去)同一个数(或式子),结果仍是等式
数学表示:
如果a=b, 那么a±c=b±c
练习1. 用适当的数或式子填空,使结果仍是等式。
(1) 若 4x = 7x – 5
4x _____= 7x_____
则 4x + = 7x
(2) 若 3a + 4 = 8
3a _____= 8 +______.
则 3a = 8 + .
5
(-4)
平衡的天平
×3 ×3
等 式
a = b
如果a=b,那么ac=____
bc
再观察 再小结
÷3 ÷3
如果 a = b
那么
a b
c c
__ __
=
( c≠0)
等 式
a = b
平衡的天平
等式性质2 :
等式两边同乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc
如果a=b (c≠0),那么
数学表示:
练习2. 用适当的数或式子填空,使结果仍是等式。
除以 - 0.5
- 4
减去1
2
除2以
1
除以3
-3
(1) 3x = - 9
(2) - 0.5x = 2
(3) 2x + 1 = 3
两边都____
两边都____
得 x = ____
得 x = ____
两边都_____
两边都____
得 2x =______
得x = _______
应用
1:用适当的数或整式填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形(改变式子的形状)的。
①、如果2x = 5 - 3x,那么2x +( )= 5
②、如果0.2x = 10, 那么x =( )
解:①、2x +( 3x )= 5
根据等式性质 1,等式两边都加上 3x。
②、x = 50
根据等式性质 2,等式两边都除以 0.2 或除以 乘以 5 。
应用
2. 已知:X=Y , 字母a可取任何值
(1)等式X-5=Y-5成立吗?为什么?
(2)等式X-(5-a)=Y-(5-a)一定成立吗?为什么?
(3)等式5X=5Y成立吗?为什么?
(4)等式X(5-a)=Y(5-a)一定成立吗?为什么?
(5)等式- =- 成立吗?为什么?
(6)等式—— =—— 一定成立吗?为什么?
X
Y
X
5-a
Y
5-a
(成立)
(成立)
(以上两题等式性质1)
(成立)
(成立)
(成立)
(3、4、5题等式性质2)
(不一定成立)
当a=5时等式两边都没有意义
册P81:
1、2、3、4
如果 ,那么 ( )
如果 ,那么 ( )
如果 ,那么 ( )
如果 ,那么 ( )
如果 ,那么 ( )
如果 , , 那么 ( )
练一练:判断对错,对的请说出根据等式的哪一条性质,错的请说出为什么。
√
×
×
×
√
√
练中获能
例1:解方程: x+7=26
x=?
两边同时减7
分析:
要使方程x+7=26转化为x=a
(即a为常数、x的系数为1的形式),
则要去掉方程左边的7.
解方程: x+7=26
解:两边同时_____,得
x=19
注:“解方程”就是利用等式性质求方程中
未知数的值,把原方程化成X=a的形式
(即x的系数是1为止)
∴
减7
x+7-7=26- 7
例2:利用等式的性质解下列方程
解:两边同时________,得
∴
导中释惑
除以-5
例2:利用等式的性质解下列方程
解:两边同时加5,得
化简,得
两边同时乘-3,得
∴
解:两边同加5,得
化简,得
两边同乘-3,得
解:两边同乘-3,得
化简,得
两边同减15,得
解法一:
解法二:
例2:检验方程的解
检验:
将
代入方程
,得:
边
即 左边=右边
是方程
的解。
左
∴
作业:P83
练习(1)(2)(3)(4)
1、利用等式的性质解下列方程并检验
解:两边同时加5,得
方程
检验:把
代入
左边
左边=右边
,得:
是方程的解
测中释惑
∴
∴
1、利用等式的性质解下列方程并检验
解:两边同时除以0.3,得
∴
方程
检验:把
代入
左边
左边=右边
,得:
∴
是方程的解
测中释惑
1、利用等式的性质解下列方程并检验
解:两边同时减4,得:
化简得:
两边同时除以5,得:
方程
检验:
左边
左边=右边
,得:
∴
是方程的解
把
代入
测中释惑
1、利用等式的性质解下列方程并检验
解:两边同时减2,得:
化简得:
两边同时乘-4,得:
方程
检验:
左边
右边
,得:
所以
是方程的解
把
代入
测中释惑
作业:利用等式的性质解下列方程并检验:
(1) x-9=6 (2) x+5=8
(3) -0.2x=10 (4) -2x+1=3
(5) 6x-2=0 (6) -x-1=0
(7) 3-2x=2 (8) -2- x=2
(9) 4(x+1)=-20 (10) = 1
学习完本课之后你有什么收获?
1、等式的性质有几条?用字母怎样表示?
2、解方程最终必须将方程化作什么形式?
悟中求真
等式的性质
1: 等式两边加(或减)同一个数
(或式子),结果仍相等。
如果 a = b
那么 a + c = b + c
2: 等式两边乘同一个数或 除以
同一个不为0的数,结果仍相等。
如果 a = b 那么 ac = bc
如果 a = b 那么
a b
c c
__ __
=
(c≠0)
掌握关键:
<1> “两 边” “同一个数(或式子) ”
<2> “除以同一个不为0的数”
小结
解方程的目标: 变形 x = a (常数)
检验的方法
(代 入)
原方程
动一动脑筋
若方程1.2x=6和2x+a=ax的解相同,你能求出a的值吗?
想一想:你会解一元一次方程了吗?我们可以用一
元一次方程求几个未知数的值呢?
作业:
习题3.1第4、9、10题
下课了,休息一会儿吧。
一元一次方程的定义:
化简后只含有一个未知数(元),并且未知数的指数是1(次)的整式方程叫一元一次方程.
注意:1、一定是化简后只含一个未知数
2、分母一定不含未知数
方程
一元一次方程
.判断下列各式哪些是方程,哪些是一元一次方程?
随堂练习
1
1.填空
(1)如果关于x的方程3x5-2k-3=0是一元一次方程,则k= ;
(2)已知方程 -(m-1)y|m|+3=0是一元一次方程,则m= 。
当堂测试
1
2
-1
如果x=62,
方程左边=2×62-5 =119,
右边=121,
左边≠右边
如果x=63,
方程左边=2 ×63-5=121,
右边=121,
左边=右边
使方程两边的值相等的未知数的值叫做方程的解
x = 63是方程2x-5=121的解
∴
∴
想一想:
关于x的方程 3x – 10 = mx 的解为2,
那么你知道m的值是多少吗,为什么?
3.1.2 等式的性质
判断下列各式是否为等式?
学中感知
你能用自己的方法求下列方程
的解吗?
很简单,就是
到底是什么呢?
学中感知
探究等式性质1
学中获知
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
等 式
a = b
+ +
平衡的天平
等 式
a +c = b+c
小结:平衡的天平两边都
加上同样的量,天平依然平
衡
结论:等式两边加上同一个数
(或同一个式子)结果仍相等
︴
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
探究等式性质1
学中获知
等 式
a = b
结论:平衡的天平两边都减去
同样的量。天平依然平衡。
结论: 等式两边都减去同一个
数(或式子)。结果仍相等。
- -
平衡的天平
等 式
a -c = b-c
︴
等式性质1:
等式两边加(或减去)同一个数(或式子),结果仍是等式
数学表示:
如果a=b, 那么a±c=b±c
练习1. 用适当的数或式子填空,使结果仍是等式。
(1) 若 4x = 7x – 5
4x _____= 7x_____
则 4x + = 7x
(2) 若 3a + 4 = 8
3a _____= 8 +______.
则 3a = 8 + .
5
(-4)
平衡的天平
×3 ×3
等 式
a = b
如果a=b,那么ac=____
bc
再观察 再小结
÷3 ÷3
如果 a = b
那么
a b
c c
__ __
=
( c≠0)
等 式
a = b
平衡的天平
等式性质2 :
等式两边同乘同一个数,或除以同一个不为0的数,结果仍相等.
如果a=b,那么ac=bc
如果a=b (c≠0),那么
数学表示:
练习2. 用适当的数或式子填空,使结果仍是等式。
除以 - 0.5
- 4
减去1
2
除2以
1
除以3
-3
(1) 3x = - 9
(2) - 0.5x = 2
(3) 2x + 1 = 3
两边都____
两边都____
得 x = ____
得 x = ____
两边都_____
两边都____
得 2x =______
得x = _______
应用
1:用适当的数或整式填空,使所得结果仍是等式,并说明是根据等式的哪一条性质以及怎样变形(改变式子的形状)的。
①、如果2x = 5 - 3x,那么2x +( )= 5
②、如果0.2x = 10, 那么x =( )
解:①、2x +( 3x )= 5
根据等式性质 1,等式两边都加上 3x。
②、x = 50
根据等式性质 2,等式两边都除以 0.2 或除以 乘以 5 。
应用
2. 已知:X=Y , 字母a可取任何值
(1)等式X-5=Y-5成立吗?为什么?
(2)等式X-(5-a)=Y-(5-a)一定成立吗?为什么?
(3)等式5X=5Y成立吗?为什么?
(4)等式X(5-a)=Y(5-a)一定成立吗?为什么?
(5)等式- =- 成立吗?为什么?
(6)等式—— =—— 一定成立吗?为什么?
X
Y
X
5-a
Y
5-a
(成立)
(成立)
(以上两题等式性质1)
(成立)
(成立)
(成立)
(3、4、5题等式性质2)
(不一定成立)
当a=5时等式两边都没有意义
册P81:
1、2、3、4
如果 ,那么 ( )
如果 ,那么 ( )
如果 ,那么 ( )
如果 ,那么 ( )
如果 ,那么 ( )
如果 , , 那么 ( )
练一练:判断对错,对的请说出根据等式的哪一条性质,错的请说出为什么。
√
×
×
×
√
√
练中获能
例1:解方程: x+7=26
x=?
两边同时减7
分析:
要使方程x+7=26转化为x=a
(即a为常数、x的系数为1的形式),
则要去掉方程左边的7.
解方程: x+7=26
解:两边同时_____,得
x=19
注:“解方程”就是利用等式性质求方程中
未知数的值,把原方程化成X=a的形式
(即x的系数是1为止)
∴
减7
x+7-7=26- 7
例2:利用等式的性质解下列方程
解:两边同时________,得
∴
导中释惑
除以-5
例2:利用等式的性质解下列方程
解:两边同时加5,得
化简,得
两边同时乘-3,得
∴
解:两边同加5,得
化简,得
两边同乘-3,得
解:两边同乘-3,得
化简,得
两边同减15,得
解法一:
解法二:
例2:检验方程的解
检验:
将
代入方程
,得:
边
即 左边=右边
是方程
的解。
左
∴
作业:P83
练习(1)(2)(3)(4)
1、利用等式的性质解下列方程并检验
解:两边同时加5,得
方程
检验:把
代入
左边
左边=右边
,得:
是方程的解
测中释惑
∴
∴
1、利用等式的性质解下列方程并检验
解:两边同时除以0.3,得
∴
方程
检验:把
代入
左边
左边=右边
,得:
∴
是方程的解
测中释惑
1、利用等式的性质解下列方程并检验
解:两边同时减4,得:
化简得:
两边同时除以5,得:
方程
检验:
左边
左边=右边
,得:
∴
是方程的解
把
代入
测中释惑
1、利用等式的性质解下列方程并检验
解:两边同时减2,得:
化简得:
两边同时乘-4,得:
方程
检验:
左边
右边
,得:
所以
是方程的解
把
代入
测中释惑
作业:利用等式的性质解下列方程并检验:
(1) x-9=6 (2) x+5=8
(3) -0.2x=10 (4) -2x+1=3
(5) 6x-2=0 (6) -x-1=0
(7) 3-2x=2 (8) -2- x=2
(9) 4(x+1)=-20 (10) = 1
学习完本课之后你有什么收获?
1、等式的性质有几条?用字母怎样表示?
2、解方程最终必须将方程化作什么形式?
悟中求真
等式的性质
1: 等式两边加(或减)同一个数
(或式子),结果仍相等。
如果 a = b
那么 a + c = b + c
2: 等式两边乘同一个数或 除以
同一个不为0的数,结果仍相等。
如果 a = b 那么 ac = bc
如果 a = b 那么
a b
c c
__ __
=
(c≠0)
掌握关键:
<1> “两 边” “同一个数(或式子) ”
<2> “除以同一个不为0的数”
小结
解方程的目标: 变形 x = a (常数)
检验的方法
(代 入)
原方程
动一动脑筋
若方程1.2x=6和2x+a=ax的解相同,你能求出a的值吗?
想一想:你会解一元一次方程了吗?我们可以用一
元一次方程求几个未知数的值呢?
作业:
习题3.1第4、9、10题
下课了,休息一会儿吧。
