3.1.2 复数的几何意义
图片预览










文档简介
课件46张PPT。3.1.2 复数的几何意义第三章 §3.1 数系的扩充和复数的概念学习目标
1.了解复数z、复平面内的点Z、向量 之间的一一对应关系.
2.理解并掌握复数的几何意义.
3.通过对复数的几何意义的学习,了解“数与形”之间的联系,提高用数形结合思想解决问题的能力.问题导学达标检测题型探究内容索引问题导学知识点一 复平面的定义思考1 实数可用数轴上的点来表示,类比一下,复数怎样来表示呢?答案 任何一个复数z=a+bi,都和一个有序实数对(a,b)一一对应,因此,复数集与平面直角坐标系中的点集之间可以建立一一对应的关系.思考2 判断下列命题的真假:
①在复平面内,对应于实数的点都在实轴上;
②在复平面内,对应于纯虚数的点都在虚轴上;
③在复平面内,实轴上的点所对应的复数都是实数;
④在复平面内,虚轴上的点所对应的复数都是纯虚数;
⑤在复平面内,对应于非纯虚数的点都分布在四个象限.答案 ①②③正确,④⑤错误.
因为原点在虚轴上,而其表示实数,所以④错.
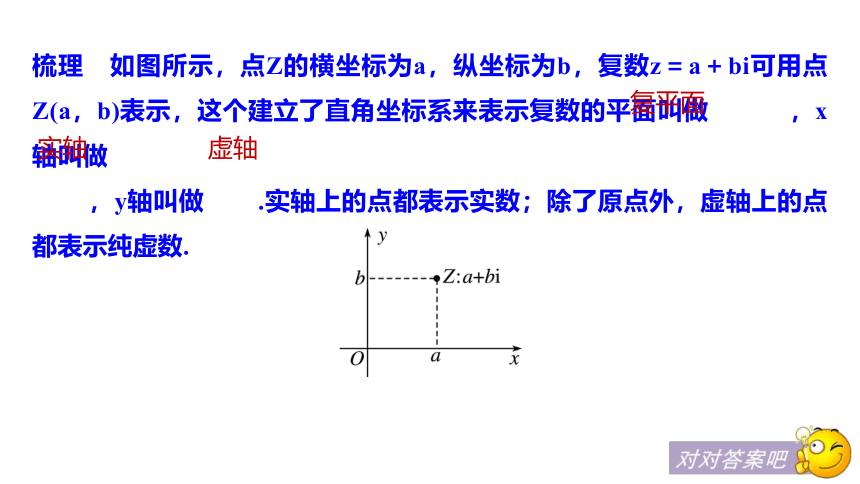
因为非纯虚数包括实数,而实数对应的点在实轴上,所以⑤错.梳理 如图所示,点Z的横坐标为a,纵坐标为b,复数z=a+bi可用点Z(a,b)表示,这个建立了直角坐标系来表示复数的平面叫做 ,x轴叫做
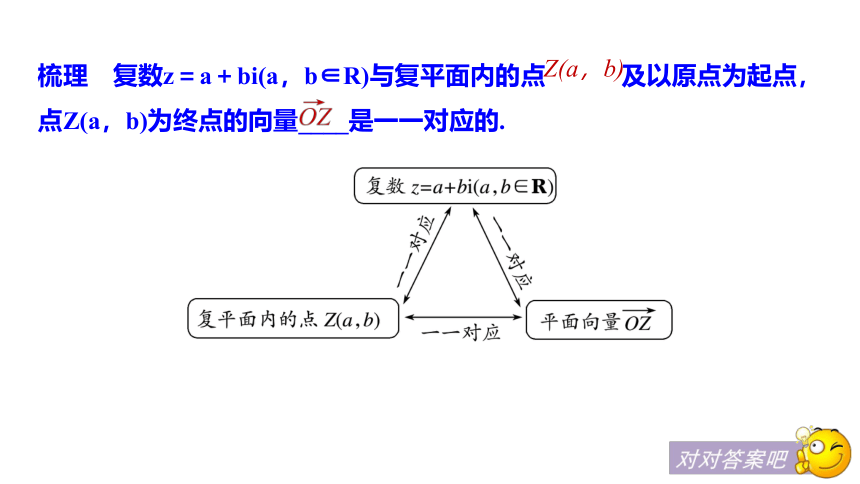
,y轴叫做 .实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.复平面虚轴实轴知识点二 复数的几何意义思考 平面向量能够与复数一一对应的前提是什么?答案 向量的起点是原点.梳理 复数z=a+bi(a,b∈R)与复平面内的点 及以原点为起点,点Z(a,b)为终点的向量____是一一对应的.Z(a,b)知识点三 复数的模思考 (1)复数的模一定是正数吗?答案 不一定,复数的模是非负数,即|z|≥0.
当z=0时,|z|=0;
反之,当|z|=0时,必有z=0.(2)若复数z满足|z|=1,则在复平面内,复数z对应的点Z的轨迹是什么?答案 点Z的轨迹是以原点为圆心,1为半径的一个圆.梳理 复数z=a+bi(a,b∈R),对应的向量为 ,则向量 的模r叫做复数z=a+bi的模,记作 或 .由模的定义可知:|z|=|a+bi|=r=
________(r≥0,r∈R).|z||a+bi|1.在复平面内,对应于实数的点都在实轴上.( )
2.若|z1|=|z2|,则z1=z2.( )[思考辨析 判断正误]√×题型探究例1 (1)对于复平面,下列说法错误的是
A.实轴上的点都表示实数,表示实数的点都在实轴上
B.虚轴上的点都表示纯虚数,表示纯虚数的点都在虚轴上
C.第一象限的点都表示实部为正数的虚数
D.实部为正数、虚部为负数的虚数对应的点必定在第四象限类型一 复平面的相关概念解析答案√解析 原点是虚轴上的点,但它表示实数.(2)下列命题为假命题的是
A.复数的模是非负实数
B.复数等于零的充要条件是它的模等于零
C.两个复数的模相等是这两个复数相等的必要条件
D.复数z1>z2的充要条件是|z1|>|z2|解析 D中两个复数不一定能比较大小,但任意两个复数的模总能比较大小,故D错.解析答案√解析答案-3i解析答案(4)已知复数z=2+i(i是虚数单位),则|z|=____.反思与感悟 确定复数对应的点在复平面内的位置时,关键是理解好复数与该点的对应关系,复数的实部就是该点的横坐标,复数的虚部就是该点的纵坐标,据此可建立复数的实部与虚部应满足的条件,通过解方程或不等式求解.跟踪训练1 已知复数z=m-2-(4-m2)i,且复数z在复平面内对应的点位于虚轴上,则实数m的值为
A.0 B.2
C.-2 D.±2解析答案解析 当点在虚轴上时,实部m-2=0,∴m=2.√类型二 复数的几何意义解答解 因为x是实数,所以x2+x-6,x2-2x-15也是实数.即当-3(1)第三象限;解答解 z=x2+x-6+(x2-2x-15)i对应点Z(x2+x-6,x2-2x-15),
当实数x满足(x2+x-6)-(x2-2x-15)-3=0,
即当x=-2时,点Z在直线x-y-3=0上.(2)直线x-y-3=0上.解答解 当实数x满足x2+x-6=0,
即当x=-3或2时,点Z在虚轴上.引申探究
若本例中的条件不变,其对应的点在:
(1)虚轴上;解答即当2A.第一象限 B.第二象限
C.第三象限 D.第四象限解析 z=(m+1)+(m-1)i对应的点为(m+1,m-1),
∵0∴点(m+1,m-1)位于第四象限.√答案解析解答类型三 复数的模则1+a2<4,所以a2<3,命题角度1 复数模的基本运算
例3 (1)如果复数z=1+ai满足条件|z|<2,那么实数a的取值范围是答案√解析答案解析反思与感悟 复数的模的几何意义是复数对应的点到原点的距离,这可以类比实数的绝对值,也可以类比以原点为起点的向量的模来加以理解.解答解 设z1=a+bi(a,b∈R),z2=c+di(c,d∈R),∵|z1|=|z2|=1,命题角度2 复数模的几何意义答案解析A.圆面
B.以点C为圆心,半径等于1的圆
C.满足方程x2+y2=1的曲线√得|z|=1,故到点C(1,2)的距离为1的点的轨迹方程为(x-1)2+(y-2)2=1,
该方程表示以点C为圆心,半径等于1的圆.反思与感悟 对于复数的模,可以从以下两个方面进行理解:一是任何复数的模都为一个非负的实数;二是复数的模表示该复数在复平面内对应的点到原点的距离.答案解析又∵复数z对应的点在第二象限,达标检测12341.复数z与它的模相等的充要条件是
A.z为纯虚数 B.z是实数
C.z是正实数 D.z是非负实数答案√5解析 由z=|z|,故z∈R且z≥0.解析解析答案123452.已知与x轴同方向的单位向量为e1,与y轴同方向的单位向量为e2,则它们对应的复数分别是
A.e1对应实数1,e2对应虚数i
B.e1对应虚数i,e2对应虚数i
C.e1对应实数1,e2对应虚数-i
D.e1对应实数1或-1,e2对应虚数i或-i√解析 e1=(1,0),e2=(0,1).解析答案123453.若复数(m2-3m-4)+(m2-5m-6)i表示的点在虚轴上,则实数m的值为________.-1或4解析 由题意知m2-3m-4=0,解得m=-1或m=4.12345答案解析12345解答5.已知复数z=3+ai,且|z|<4,求实数a的取值范围.解 方法一 ∵z=3+ai(a∈R),由已知得32+a2<42,方法二 由|z|<4知z在复平面内对应的点在以原点为圆心,以4为半径的圆内(不包括边界),由z=3+ai知z对应的点在直线x=3上,∴线段AB(除去端点)为动点Z(3,a)的集合,123451.复数的几何意义规律与方法这种对应关系架起了复数与解析几何之间的桥梁,使得复数问题可以用几何方法解决,而几何问题也可以用复数方法(即数形结合法)解决,增加了解决复数问题的途径.
(1)复数z=a+bi(a,b∈R)的对应点的坐标为(a,b)而不是(a,bi);2.复数的模(2)从几何意义上理解,表示点Z和原点间的距离,类比向量的模可进一步引申:|z1-z2|表示点Z1和点Z2之间的距离.本课结束
1.了解复数z、复平面内的点Z、向量 之间的一一对应关系.
2.理解并掌握复数的几何意义.
3.通过对复数的几何意义的学习,了解“数与形”之间的联系,提高用数形结合思想解决问题的能力.问题导学达标检测题型探究内容索引问题导学知识点一 复平面的定义思考1 实数可用数轴上的点来表示,类比一下,复数怎样来表示呢?答案 任何一个复数z=a+bi,都和一个有序实数对(a,b)一一对应,因此,复数集与平面直角坐标系中的点集之间可以建立一一对应的关系.思考2 判断下列命题的真假:
①在复平面内,对应于实数的点都在实轴上;
②在复平面内,对应于纯虚数的点都在虚轴上;
③在复平面内,实轴上的点所对应的复数都是实数;
④在复平面内,虚轴上的点所对应的复数都是纯虚数;
⑤在复平面内,对应于非纯虚数的点都分布在四个象限.答案 ①②③正确,④⑤错误.
因为原点在虚轴上,而其表示实数,所以④错.
因为非纯虚数包括实数,而实数对应的点在实轴上,所以⑤错.梳理 如图所示,点Z的横坐标为a,纵坐标为b,复数z=a+bi可用点Z(a,b)表示,这个建立了直角坐标系来表示复数的平面叫做 ,x轴叫做
,y轴叫做 .实轴上的点都表示实数;除了原点外,虚轴上的点都表示纯虚数.复平面虚轴实轴知识点二 复数的几何意义思考 平面向量能够与复数一一对应的前提是什么?答案 向量的起点是原点.梳理 复数z=a+bi(a,b∈R)与复平面内的点 及以原点为起点,点Z(a,b)为终点的向量____是一一对应的.Z(a,b)知识点三 复数的模思考 (1)复数的模一定是正数吗?答案 不一定,复数的模是非负数,即|z|≥0.
当z=0时,|z|=0;
反之,当|z|=0时,必有z=0.(2)若复数z满足|z|=1,则在复平面内,复数z对应的点Z的轨迹是什么?答案 点Z的轨迹是以原点为圆心,1为半径的一个圆.梳理 复数z=a+bi(a,b∈R),对应的向量为 ,则向量 的模r叫做复数z=a+bi的模,记作 或 .由模的定义可知:|z|=|a+bi|=r=
________(r≥0,r∈R).|z||a+bi|1.在复平面内,对应于实数的点都在实轴上.( )
2.若|z1|=|z2|,则z1=z2.( )[思考辨析 判断正误]√×题型探究例1 (1)对于复平面,下列说法错误的是
A.实轴上的点都表示实数,表示实数的点都在实轴上
B.虚轴上的点都表示纯虚数,表示纯虚数的点都在虚轴上
C.第一象限的点都表示实部为正数的虚数
D.实部为正数、虚部为负数的虚数对应的点必定在第四象限类型一 复平面的相关概念解析答案√解析 原点是虚轴上的点,但它表示实数.(2)下列命题为假命题的是
A.复数的模是非负实数
B.复数等于零的充要条件是它的模等于零
C.两个复数的模相等是这两个复数相等的必要条件
D.复数z1>z2的充要条件是|z1|>|z2|解析 D中两个复数不一定能比较大小,但任意两个复数的模总能比较大小,故D错.解析答案√解析答案-3i解析答案(4)已知复数z=2+i(i是虚数单位),则|z|=____.反思与感悟 确定复数对应的点在复平面内的位置时,关键是理解好复数与该点的对应关系,复数的实部就是该点的横坐标,复数的虚部就是该点的纵坐标,据此可建立复数的实部与虚部应满足的条件,通过解方程或不等式求解.跟踪训练1 已知复数z=m-2-(4-m2)i,且复数z在复平面内对应的点位于虚轴上,则实数m的值为
A.0 B.2
C.-2 D.±2解析答案解析 当点在虚轴上时,实部m-2=0,∴m=2.√类型二 复数的几何意义解答解 因为x是实数,所以x2+x-6,x2-2x-15也是实数.即当-3
当实数x满足(x2+x-6)-(x2-2x-15)-3=0,
即当x=-2时,点Z在直线x-y-3=0上.(2)直线x-y-3=0上.解答解 当实数x满足x2+x-6=0,
即当x=-3或2时,点Z在虚轴上.引申探究
若本例中的条件不变,其对应的点在:
(1)虚轴上;解答即当2
C.第三象限 D.第四象限解析 z=(m+1)+(m-1)i对应的点为(m+1,m-1),
∵0
例3 (1)如果复数z=1+ai满足条件|z|<2,那么实数a的取值范围是答案√解析答案解析反思与感悟 复数的模的几何意义是复数对应的点到原点的距离,这可以类比实数的绝对值,也可以类比以原点为起点的向量的模来加以理解.解答解 设z1=a+bi(a,b∈R),z2=c+di(c,d∈R),∵|z1|=|z2|=1,命题角度2 复数模的几何意义答案解析A.圆面
B.以点C为圆心,半径等于1的圆
C.满足方程x2+y2=1的曲线√得|z|=1,故到点C(1,2)的距离为1的点的轨迹方程为(x-1)2+(y-2)2=1,
该方程表示以点C为圆心,半径等于1的圆.反思与感悟 对于复数的模,可以从以下两个方面进行理解:一是任何复数的模都为一个非负的实数;二是复数的模表示该复数在复平面内对应的点到原点的距离.答案解析又∵复数z对应的点在第二象限,达标检测12341.复数z与它的模相等的充要条件是
A.z为纯虚数 B.z是实数
C.z是正实数 D.z是非负实数答案√5解析 由z=|z|,故z∈R且z≥0.解析解析答案123452.已知与x轴同方向的单位向量为e1,与y轴同方向的单位向量为e2,则它们对应的复数分别是
A.e1对应实数1,e2对应虚数i
B.e1对应虚数i,e2对应虚数i
C.e1对应实数1,e2对应虚数-i
D.e1对应实数1或-1,e2对应虚数i或-i√解析 e1=(1,0),e2=(0,1).解析答案123453.若复数(m2-3m-4)+(m2-5m-6)i表示的点在虚轴上,则实数m的值为________.-1或4解析 由题意知m2-3m-4=0,解得m=-1或m=4.12345答案解析12345解答5.已知复数z=3+ai,且|z|<4,求实数a的取值范围.解 方法一 ∵z=3+ai(a∈R),由已知得32+a2<42,方法二 由|z|<4知z在复平面内对应的点在以原点为圆心,以4为半径的圆内(不包括边界),由z=3+ai知z对应的点在直线x=3上,∴线段AB(除去端点)为动点Z(3,a)的集合,123451.复数的几何意义规律与方法这种对应关系架起了复数与解析几何之间的桥梁,使得复数问题可以用几何方法解决,而几何问题也可以用复数方法(即数形结合法)解决,增加了解决复数问题的途径.
(1)复数z=a+bi(a,b∈R)的对应点的坐标为(a,b)而不是(a,bi);2.复数的模(2)从几何意义上理解,表示点Z和原点间的距离,类比向量的模可进一步引申:|z1-z2|表示点Z1和点Z2之间的距离.本课结束
