3.2.1 复数代数形式的加减运算及其几何意义
文档属性
| 名称 | 3.2.1 复数代数形式的加减运算及其几何意义 |  | |
| 格式 | zip | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 11:38:56 | ||
图片预览










文档简介
课件31张PPT。3.2.1 复数代数形式的加减运算及其几何意义第三章 §3.2 复数代数形式的四则运算学习目标
1.理解并掌握复数代数形式的加减运算法则.
2.了解复数代数形式的加法、减法的几何意义,掌握不同数集中加减运算法则的联系与区别.
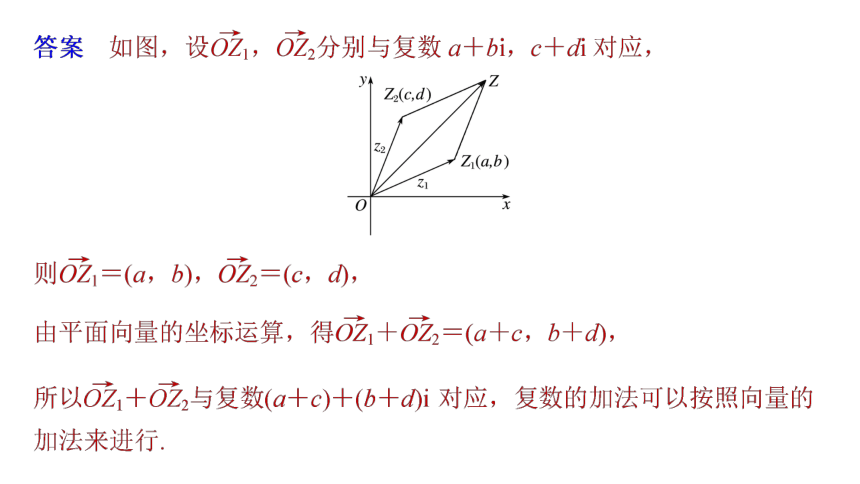
3.在研究复数代数形式的加法、减法的几何意义时,充分利用向量加法、减法的性质.问题导学达标检测题型探究内容索引问题导学知识点一 复数代数形式的加减法思考1 类比多项式的加减法运算,想一想复数如何进行加减法运算?答案 两个复数相加(减)就是把实部与实部、虚部与虚部分别相加(减),即(a+bi)±(c+di)=(a±c)+(b±d)i.思考2 若复数z1,z2满足z1-z2>0,能否认为z1>z2?答案 不能,如2+i-i>0,但2+i与i不能比较大小.梳理 (1)运算法则
设z1=a+bi,z2=c+di是任意两个复数,那么(a+bi)+(c+di)=_______
,(a+bi)-(c+di)= .
(2)加法运算律
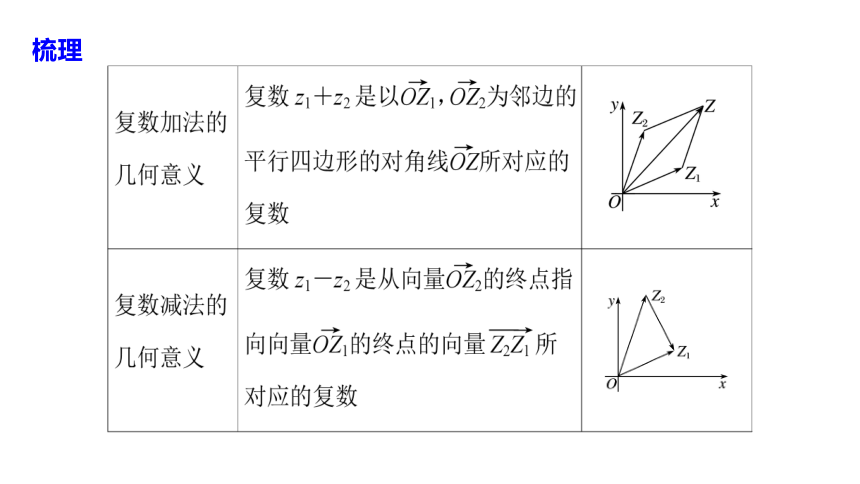
对任意z1,z2,z3∈C,有z1+z2= ,(z1+z2)+z3= .(a+c)+(a-c)+(b-d)iz2+z1z1+(z2+z3)(b+d)i知识点二 复数加减法的几何意义思考1 复数与复平面内的向量一一对应,你能从向量加法的几何意义出发讨论复数加法的几何意义吗?思考2 怎样作出与复数z1-z2对应的向量?梳理1.两个虚数的和或差可能是实数.( )
2.在进行复数的加法时,实部与实部相加得实部,虚部与虚部相加得虚部.
( )
3.复数的减法不满足结合律,即(z1-z2)-z3=z1-(z2+z3)可能不成立.
( )[思考辨析 判断正误]√√×题型探究类型一 复数的加、减法运算解答(3)(6-3i)+(3+2i)-(3-4i)-(-2+i).解 (6-3i)+(3+2i)-(3-4i)-(-2+i)=[6+3-3-(-2)]+[-3+2-(-4)-1]i=8+2i.反思与感悟 (1)复数的加减运算就是实部与实部相加减,虚部与虚部相加减.
(2)当一个等式中同时含有|z|与z时,一般用待定系数法,设z=x+yi(x,y∈R).跟踪训练1 (1)若复数z满足z+i-3=3-i,则z=_____.解析 ∵z+i-3=3-i,∴z=6-2i.解析答案6-2i(2)(a+bi)-(2a-3bi)-3i=_____________(a,b∈R).-a+(4b-3)i解析 (a+bi)-(2a-3bi)-3i
=(a-2a)+(b+3b-3)i=-a+(4b-3)i.解析答案∴z=-4+3i.(3)已知复数z满足|z|+z=1+3i,则z=________.-4+3i类型二 复数加、减法的几何意义解答解 z1-z2=(-2+i)-(-1+2i)=-1-i.例2 已知复数z1=-2+i,z2=-1+2i.
(1)求z1-z2;(2)在复平面内作出z1-z2的运算结果所对应的向量.反思与感悟 复数的减法可以用向量来运算,同样可以运用平行四边形法则和三角形法则进行运算.跟踪训练2 已知z1=2+i,z2=1-2i,则复数z=z2-z1在复平面内对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限答案√解析 z=z2-z1=(1-2i)-(2+i)=-1-3i,
故复数z在复平面内对应的点的坐标为(-1,-3),故选C.解析类型三 复数加、减法及其几何意义的综合运用解答解 由已知得,在复平面内复数z对应的点Z在以原点为圆心,半径为2的圆上.跟踪训练3 在平行四边形ABCD中,点A,B,C对应的复数分别为4+i,3+4i,3-5i,则点D对应的复数是
A.2-3i B.4+8i
C.4-8i D.1+4i答案√解析∴z=(3-5i)-(-1+3i)=(3+1)+(-5-3)i=4-8i.达标检测12341.计算(3+i)-(2+i)的结果为
A.1 B.-i
C.5+2i D.1-i答案√5解析 (3+i)-(2+i)=1.解析解析答案12345√解析答案√123454.若z1=x1+y1i,z2=x2+y2i(x1,x2,y1,y2∈R),则|z2-z1|=
__________________.12345答案解析 ∵z1=x1+y1i,z2=x2+y2i,
∴z2-z1=(x2-x1)+(y2-y1)i,解析12345答案解析5.若复数z1+z2=3+4i,z1-z2=5-2i,则2z1=______.8+2i解析 两式相加得2z1=8+2i.1.复数代数形式的加减法满足交换律、结合律,复数的减法是加法的逆运算.
2.复数加法的几何意义就是向量加法的平行四边形法则,复数减法的几何意义就是向量减法的三角形法则.本课结束
1.理解并掌握复数代数形式的加减运算法则.
2.了解复数代数形式的加法、减法的几何意义,掌握不同数集中加减运算法则的联系与区别.
3.在研究复数代数形式的加法、减法的几何意义时,充分利用向量加法、减法的性质.问题导学达标检测题型探究内容索引问题导学知识点一 复数代数形式的加减法思考1 类比多项式的加减法运算,想一想复数如何进行加减法运算?答案 两个复数相加(减)就是把实部与实部、虚部与虚部分别相加(减),即(a+bi)±(c+di)=(a±c)+(b±d)i.思考2 若复数z1,z2满足z1-z2>0,能否认为z1>z2?答案 不能,如2+i-i>0,但2+i与i不能比较大小.梳理 (1)运算法则
设z1=a+bi,z2=c+di是任意两个复数,那么(a+bi)+(c+di)=_______
,(a+bi)-(c+di)= .
(2)加法运算律
对任意z1,z2,z3∈C,有z1+z2= ,(z1+z2)+z3= .(a+c)+(a-c)+(b-d)iz2+z1z1+(z2+z3)(b+d)i知识点二 复数加减法的几何意义思考1 复数与复平面内的向量一一对应,你能从向量加法的几何意义出发讨论复数加法的几何意义吗?思考2 怎样作出与复数z1-z2对应的向量?梳理1.两个虚数的和或差可能是实数.( )
2.在进行复数的加法时,实部与实部相加得实部,虚部与虚部相加得虚部.
( )
3.复数的减法不满足结合律,即(z1-z2)-z3=z1-(z2+z3)可能不成立.
( )[思考辨析 判断正误]√√×题型探究类型一 复数的加、减法运算解答(3)(6-3i)+(3+2i)-(3-4i)-(-2+i).解 (6-3i)+(3+2i)-(3-4i)-(-2+i)=[6+3-3-(-2)]+[-3+2-(-4)-1]i=8+2i.反思与感悟 (1)复数的加减运算就是实部与实部相加减,虚部与虚部相加减.
(2)当一个等式中同时含有|z|与z时,一般用待定系数法,设z=x+yi(x,y∈R).跟踪训练1 (1)若复数z满足z+i-3=3-i,则z=_____.解析 ∵z+i-3=3-i,∴z=6-2i.解析答案6-2i(2)(a+bi)-(2a-3bi)-3i=_____________(a,b∈R).-a+(4b-3)i解析 (a+bi)-(2a-3bi)-3i
=(a-2a)+(b+3b-3)i=-a+(4b-3)i.解析答案∴z=-4+3i.(3)已知复数z满足|z|+z=1+3i,则z=________.-4+3i类型二 复数加、减法的几何意义解答解 z1-z2=(-2+i)-(-1+2i)=-1-i.例2 已知复数z1=-2+i,z2=-1+2i.
(1)求z1-z2;(2)在复平面内作出z1-z2的运算结果所对应的向量.反思与感悟 复数的减法可以用向量来运算,同样可以运用平行四边形法则和三角形法则进行运算.跟踪训练2 已知z1=2+i,z2=1-2i,则复数z=z2-z1在复平面内对应的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限答案√解析 z=z2-z1=(1-2i)-(2+i)=-1-3i,
故复数z在复平面内对应的点的坐标为(-1,-3),故选C.解析类型三 复数加、减法及其几何意义的综合运用解答解 由已知得,在复平面内复数z对应的点Z在以原点为圆心,半径为2的圆上.跟踪训练3 在平行四边形ABCD中,点A,B,C对应的复数分别为4+i,3+4i,3-5i,则点D对应的复数是
A.2-3i B.4+8i
C.4-8i D.1+4i答案√解析∴z=(3-5i)-(-1+3i)=(3+1)+(-5-3)i=4-8i.达标检测12341.计算(3+i)-(2+i)的结果为
A.1 B.-i
C.5+2i D.1-i答案√5解析 (3+i)-(2+i)=1.解析解析答案12345√解析答案√123454.若z1=x1+y1i,z2=x2+y2i(x1,x2,y1,y2∈R),则|z2-z1|=
__________________.12345答案解析 ∵z1=x1+y1i,z2=x2+y2i,
∴z2-z1=(x2-x1)+(y2-y1)i,解析12345答案解析5.若复数z1+z2=3+4i,z1-z2=5-2i,则2z1=______.8+2i解析 两式相加得2z1=8+2i.1.复数代数形式的加减法满足交换律、结合律,复数的减法是加法的逆运算.
2.复数加法的几何意义就是向量加法的平行四边形法则,复数减法的几何意义就是向量减法的三角形法则.本课结束
