3.2.2 复数代数形式的乘除运算
文档属性
| 名称 | 3.2.2 复数代数形式的乘除运算 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 00:00:00 | ||
图片预览











文档简介
课件45张PPT。3.2.2 复数代数形式的乘除运算第三章 §3.2 复数代数形式的四则运算学习目标
1.掌握复数代数形式的四则运算法则,熟练地运用复数的乘法、除法的运算法则.
2.理解复数乘法的交换律、结合律、分配律.
3.理解并掌握共轭复数的性质及应用.问题导学达标检测题型探究内容索引问题导学知识点一 复数的乘法及运算律思考 请你探究in(n∈N*)的取值情况及其规律.答案 in(n∈N*)的取值只有i,-1,-i,1,且具有周期性,具体取值规律为:i4k+1=i,i4k+2=-1,i4k+3=-i,i4k=1,k∈N.梳理 (1)复数的乘法法则
设z1=a+bi,z2=c+di是任意两个复数,那么它们的积
(a+bi)(c+di)= .
(2)复数乘法的运算律
对于任意z1,z2,z3∈C,有(ac-bd)+(ad+bc)iz2z1z1(z2z3)z1z2+z1z3知识点二 共轭复数思考 当两个复数互为共轭复数时,它们的乘积是一个怎样的数?与复数的模的关系是什么?梳理 (1)共轭复数的概念
一般地,当两个复数的 时,这两个复数叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做 .z的共轭复数用___表示.若z=a+bi(a,b∈R),则 = .
(2)共轭复数的性质
①在复平面内,两个共轭复数对应的点关于 对称.
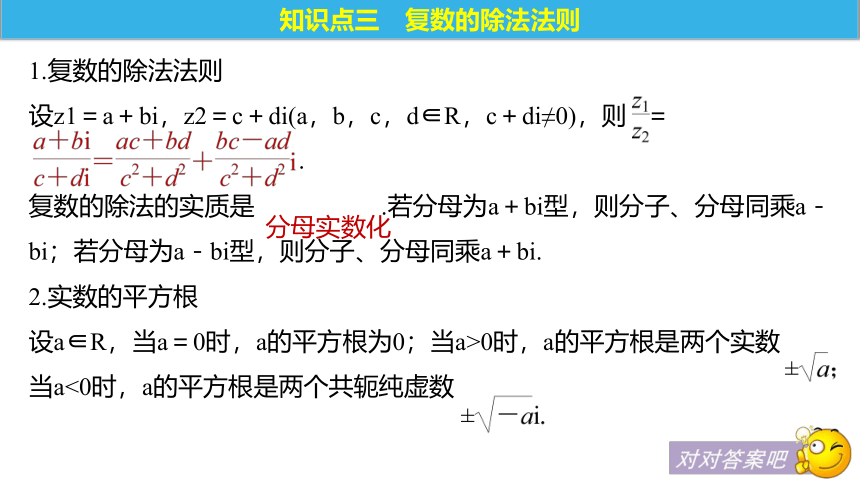
②实数的共轭复数是 ,即z= ?z∈R,利用这个性质可证明一个复数为实数.实部相等,虚部互为相反数共轭虚数实轴它本身a-bi③若z≠0且z+ =0,则z为 ,利用这个性质,可证明一个复数为纯虚数.纯虚数知识点三 复数的除法法则1.复数的除法法则
设z1=a+bi,z2=c+di(a,b,c,d∈R,c+di≠0),则 =
.
复数的除法的实质是 .若分母为a+bi型,则分子、分母同乘a-bi;若分母为a-bi型,则分子、分母同乘a+bi.
2.实数的平方根
设a∈R,当a=0时,a的平方根为0;当a>0时,a的平方根是两个实数
当a<0时,a的平方根是两个共轭纯虚数分母实数化3.虚数的平方根1.复数加减乘除的混合运算法则是先乘除后加减.( )
2.两个共轭复数的和与积是实数.( )
3.若z1,z2∈C, 则z1=z2=0.( )[思考辨析 判断正误]√√×题型探究类型一 复数的乘、除法运算命题角度1 复数乘、除法基本运算
例1 (1)i(1-i)2的值等于
A.-4 B.2
C.-2i D.4i解析 i(1-i)2=i(-2i)=2.答案√解析解析答案(2)若复数z满足(1-z)(1+2i)=i,则在复平面内表示复数z的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限答案√解析解析答案(3)若复数z满足(1+i)·z=2i(i为虚数单位),则复数z=____.答案解析解析答案1+i反思与感悟 (1)两个复数代数形式乘法的一般运算方法:首先按多项式的乘法展开;再将i2换成-1;然后再进行复数的加、减运算,化简为复数的代数形式.
(2)常用公式
①(a+bi)2=a2+2abi-b2(a,b∈R).
②(a+bi)(a-bi)=a2+b2(a,b∈R).
③(1±i)2=±2i.解析 因为(1+i)(1-bi)=1+b+(1-b)i=a,
又a,b∈R,所以1+b=a且1-b=0,解析答案2由题意知,(x-yi)(x+yi+2)=4+3i.解答命题角度2 复数乘除法的灵活运算
例2 计算下列各式:=1+(4i)4-i25=257-i.答案解析解答答案解析解答反思与感悟 复数四则运算的解答策略
(1)复数的加法、减法、乘法运算法则可以类比多项式的运算法则,除法的关键是分子、分母同乘分母的共轭复数,解题时要注意把i的幂写成最简形式.答案解析A.i B.-i
C.22 005 D.-22 005答案√解析(2)计算:解答②1+in+i2n+…+i2 000n(n∈N*).答案解析解答解 当n=4k(k∈N*)时,原式= =2 001.当n≠4k(k∈N*)时,类型二 复数运算的综合应用解答解 设x0是方程x2-(4-2i)x+3-2i=0的实根,例3 试判断方程x2-(4-2i)x+3-2i=0是否有实根,并解该方程.解得x0=1,故该方程有实根.
根据根与系数的关系,得方程的两个根分别为1,3-2i.反思与感悟 根据复数相等的充要条件解决复系数方程是否有实根问题时,可由一个复数等式得到两个实数等式组成的方程组,从而可确定两个独立参数,化复数问题为实数问题来解决.答案解析√答案解析(2)已知复数z=-3+2i(i为虚数单位)是关于x的方程2x2+px+q=0(p,q为实数)的一个根,则p+q的值为
A.22 B.36
C.38 D.42√解析 ∵z=-3+2i是关于x的方程2x2+px+q=0的一个根,
∴2×(-3+2i)2+p(-3+2i)+q=0,
即2×(9-4-12i)-3p+2pi+q=0,
得10+q-3p+(2p-24)i=0.∴p+q=38.类型三 共轭复数的概念及其应用A.-2-i B.-2+i
C.2-i D.2+i√答案解析(2)若复数z满足(2-i)z=5i(其中i为虚数单位),则复数z的共轭复数的模是____.答案解析答案解析解析 m,n∈R,且m+2i=2-ni,
可得m=2,n=-2,i所以它的共轭复数为i.解答解 设z=a+bi(a,b∈R),∴a2+b2+2i(a+bi)=8+6i,
即a2+b2-2b+2ai=8+6i,∴a+b=4,
∴复数z的实部与虚部的和是4.达标检测12341.若复数z1=1+i,z2=3-i,则z1·z2等于
A.4+2i B.2+i
C.2+2i D.3+i答案√5解析 z1·z2=(1+i)·(3-i)=1×3-i×i+(3-1)i=4+2i.解析解析答案12345√解析答案12345-112345答案解析12345解答5.计算:=8+8-16-16i
=-16i.12345解答1.复数代数形式的乘除运算
(1)复数代数形式的乘法类似于多项式乘以多项式,复数的乘法满足交换律、结合律以及乘法对加法的分配律.
(2)在进行复数代数形式的除法运算时,通常先将除法写成分式的形式,再把分子、分母都乘以分母的共轭复数,化简后可得,类似于以前学习的分母有理化.
2.共轭复数的性质可以用来解决一些复数问题.
3.复数问题实数化思想.
复数问题实数化是解决复数问题的基本思想方法,其桥梁是设复数z=a+bi(a,b∈R),利用复数相等的充要条件转化.规律与方法本课结束
1.掌握复数代数形式的四则运算法则,熟练地运用复数的乘法、除法的运算法则.
2.理解复数乘法的交换律、结合律、分配律.
3.理解并掌握共轭复数的性质及应用.问题导学达标检测题型探究内容索引问题导学知识点一 复数的乘法及运算律思考 请你探究in(n∈N*)的取值情况及其规律.答案 in(n∈N*)的取值只有i,-1,-i,1,且具有周期性,具体取值规律为:i4k+1=i,i4k+2=-1,i4k+3=-i,i4k=1,k∈N.梳理 (1)复数的乘法法则
设z1=a+bi,z2=c+di是任意两个复数,那么它们的积
(a+bi)(c+di)= .
(2)复数乘法的运算律
对于任意z1,z2,z3∈C,有(ac-bd)+(ad+bc)iz2z1z1(z2z3)z1z2+z1z3知识点二 共轭复数思考 当两个复数互为共轭复数时,它们的乘积是一个怎样的数?与复数的模的关系是什么?梳理 (1)共轭复数的概念
一般地,当两个复数的 时,这两个复数叫做互为共轭复数.虚部不等于0的两个共轭复数也叫做 .z的共轭复数用___表示.若z=a+bi(a,b∈R),则 = .
(2)共轭复数的性质
①在复平面内,两个共轭复数对应的点关于 对称.
②实数的共轭复数是 ,即z= ?z∈R,利用这个性质可证明一个复数为实数.实部相等,虚部互为相反数共轭虚数实轴它本身a-bi③若z≠0且z+ =0,则z为 ,利用这个性质,可证明一个复数为纯虚数.纯虚数知识点三 复数的除法法则1.复数的除法法则
设z1=a+bi,z2=c+di(a,b,c,d∈R,c+di≠0),则 =
.
复数的除法的实质是 .若分母为a+bi型,则分子、分母同乘a-bi;若分母为a-bi型,则分子、分母同乘a+bi.
2.实数的平方根
设a∈R,当a=0时,a的平方根为0;当a>0时,a的平方根是两个实数
当a<0时,a的平方根是两个共轭纯虚数分母实数化3.虚数的平方根1.复数加减乘除的混合运算法则是先乘除后加减.( )
2.两个共轭复数的和与积是实数.( )
3.若z1,z2∈C, 则z1=z2=0.( )[思考辨析 判断正误]√√×题型探究类型一 复数的乘、除法运算命题角度1 复数乘、除法基本运算
例1 (1)i(1-i)2的值等于
A.-4 B.2
C.-2i D.4i解析 i(1-i)2=i(-2i)=2.答案√解析解析答案(2)若复数z满足(1-z)(1+2i)=i,则在复平面内表示复数z的点位于
A.第一象限 B.第二象限
C.第三象限 D.第四象限答案√解析解析答案(3)若复数z满足(1+i)·z=2i(i为虚数单位),则复数z=____.答案解析解析答案1+i反思与感悟 (1)两个复数代数形式乘法的一般运算方法:首先按多项式的乘法展开;再将i2换成-1;然后再进行复数的加、减运算,化简为复数的代数形式.
(2)常用公式
①(a+bi)2=a2+2abi-b2(a,b∈R).
②(a+bi)(a-bi)=a2+b2(a,b∈R).
③(1±i)2=±2i.解析 因为(1+i)(1-bi)=1+b+(1-b)i=a,
又a,b∈R,所以1+b=a且1-b=0,解析答案2由题意知,(x-yi)(x+yi+2)=4+3i.解答命题角度2 复数乘除法的灵活运算
例2 计算下列各式:=1+(4i)4-i25=257-i.答案解析解答答案解析解答反思与感悟 复数四则运算的解答策略
(1)复数的加法、减法、乘法运算法则可以类比多项式的运算法则,除法的关键是分子、分母同乘分母的共轭复数,解题时要注意把i的幂写成最简形式.答案解析A.i B.-i
C.22 005 D.-22 005答案√解析(2)计算:解答②1+in+i2n+…+i2 000n(n∈N*).答案解析解答解 当n=4k(k∈N*)时,原式= =2 001.当n≠4k(k∈N*)时,类型二 复数运算的综合应用解答解 设x0是方程x2-(4-2i)x+3-2i=0的实根,例3 试判断方程x2-(4-2i)x+3-2i=0是否有实根,并解该方程.解得x0=1,故该方程有实根.
根据根与系数的关系,得方程的两个根分别为1,3-2i.反思与感悟 根据复数相等的充要条件解决复系数方程是否有实根问题时,可由一个复数等式得到两个实数等式组成的方程组,从而可确定两个独立参数,化复数问题为实数问题来解决.答案解析√答案解析(2)已知复数z=-3+2i(i为虚数单位)是关于x的方程2x2+px+q=0(p,q为实数)的一个根,则p+q的值为
A.22 B.36
C.38 D.42√解析 ∵z=-3+2i是关于x的方程2x2+px+q=0的一个根,
∴2×(-3+2i)2+p(-3+2i)+q=0,
即2×(9-4-12i)-3p+2pi+q=0,
得10+q-3p+(2p-24)i=0.∴p+q=38.类型三 共轭复数的概念及其应用A.-2-i B.-2+i
C.2-i D.2+i√答案解析(2)若复数z满足(2-i)z=5i(其中i为虚数单位),则复数z的共轭复数的模是____.答案解析答案解析解析 m,n∈R,且m+2i=2-ni,
可得m=2,n=-2,i所以它的共轭复数为i.解答解 设z=a+bi(a,b∈R),∴a2+b2+2i(a+bi)=8+6i,
即a2+b2-2b+2ai=8+6i,∴a+b=4,
∴复数z的实部与虚部的和是4.达标检测12341.若复数z1=1+i,z2=3-i,则z1·z2等于
A.4+2i B.2+i
C.2+2i D.3+i答案√5解析 z1·z2=(1+i)·(3-i)=1×3-i×i+(3-1)i=4+2i.解析解析答案12345√解析答案12345-112345答案解析12345解答5.计算:=8+8-16-16i
=-16i.12345解答1.复数代数形式的乘除运算
(1)复数代数形式的乘法类似于多项式乘以多项式,复数的乘法满足交换律、结合律以及乘法对加法的分配律.
(2)在进行复数代数形式的除法运算时,通常先将除法写成分式的形式,再把分子、分母都乘以分母的共轭复数,化简后可得,类似于以前学习的分母有理化.
2.共轭复数的性质可以用来解决一些复数问题.
3.复数问题实数化思想.
复数问题实数化是解决复数问题的基本思想方法,其桥梁是设复数z=a+bi(a,b∈R),利用复数相等的充要条件转化.规律与方法本课结束
