第1讲 1 平行线等分线段定理
图片预览




文档简介
课件26张PPT。一 平行线等分线段定理[学习目标]1.理解平行线等分线段定理的证明过程及性质.
2.能独立证明平行线等分线段定理的推论1、推论2.
3.能应用定理和推论解决相关的几何计算问题和证明问题.[知识链接]1.三角形、梯形的中位线定理的内容是什么?
提示 (1)三角形中位线平行于第三边,并且等于它的一半.
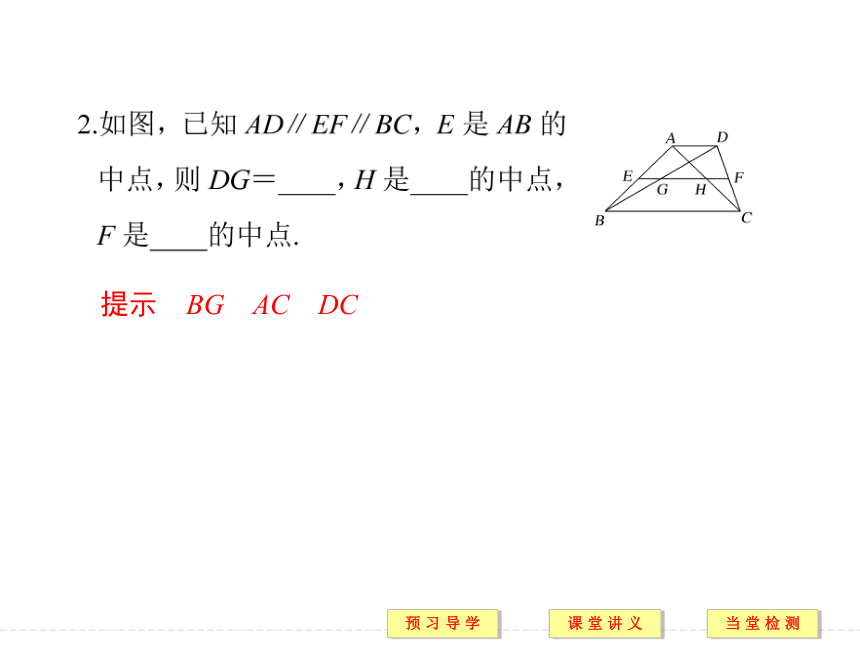
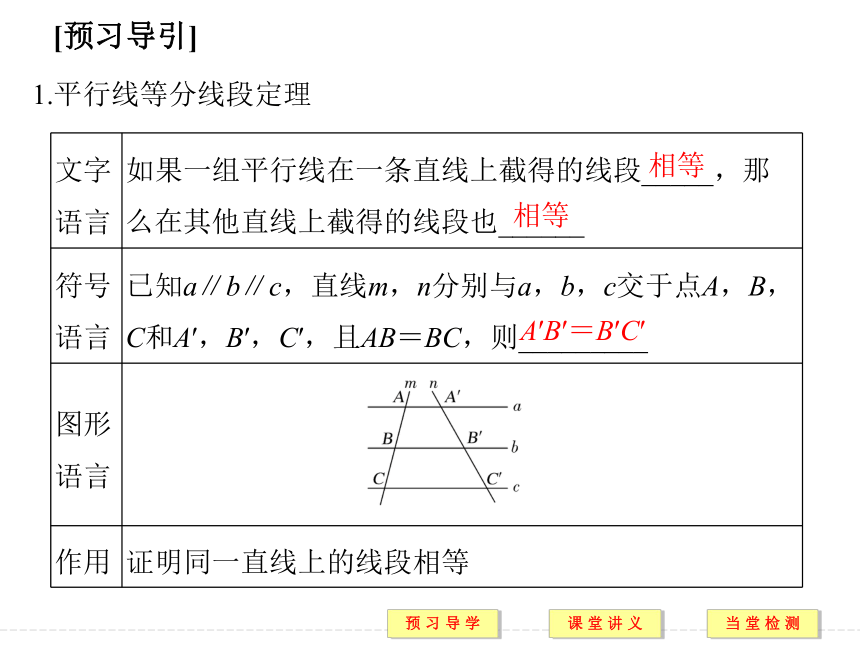
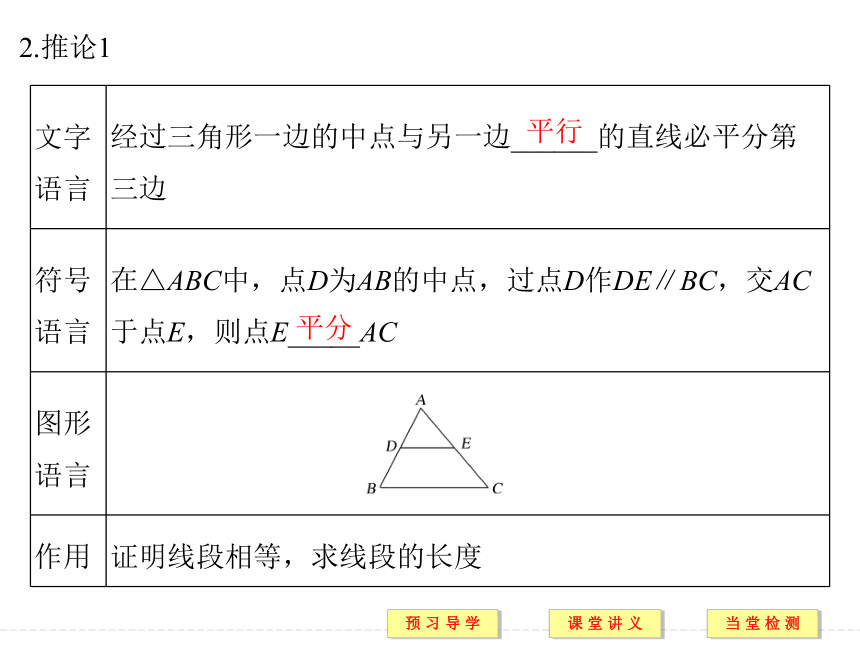
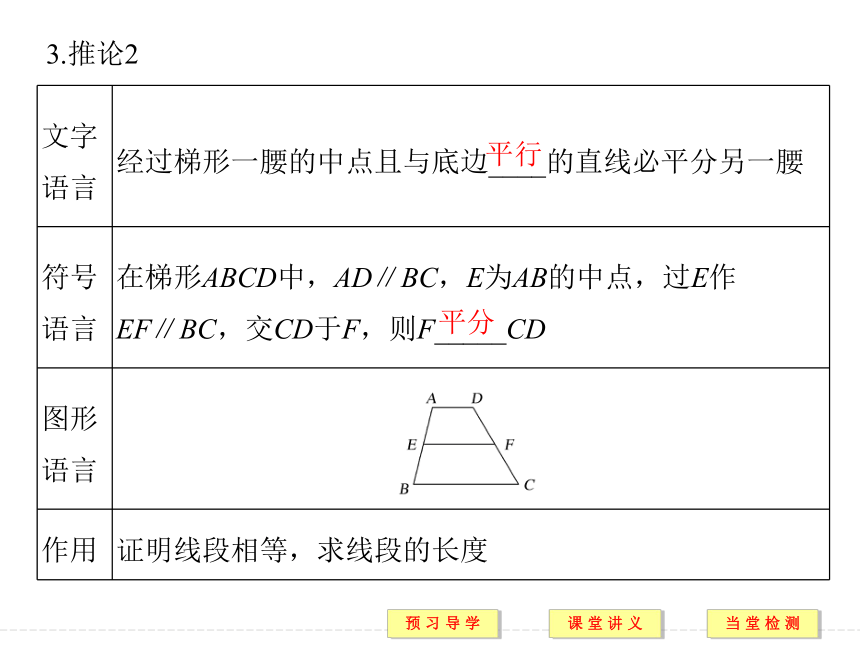
(2)梯形的中位线平行于两底,并且等于两底和的一半.提示 BG AC DC[预习导引]1.平行线等分线段定理相等相等A′B′=B′C′2.推论1平行平分3.推论2平行平分要点一 平行线等分线段定理
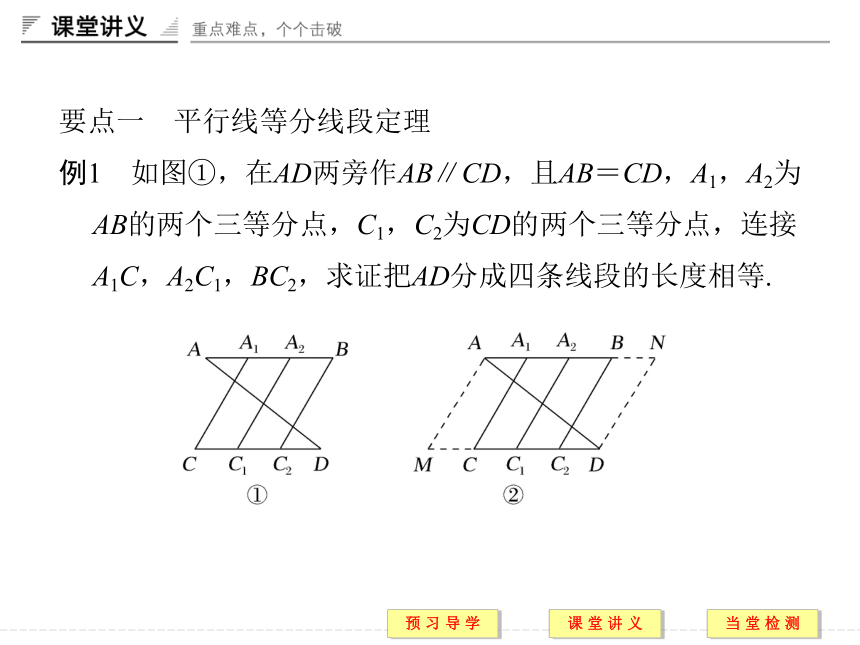
例1 如图①,在AD两旁作AB∥CD,且AB=CD,A1,A2为AB的两个三等分点,C1,C2为CD的两个三等分点,连接A1C,A2C1,BC2,求证把AD分成四条线段的长度相等.证明 如图②,过点A作直线AM平行于A1C,延长DC交AM于点M,过点D作直线DN平行于BC2,延长AB交DN于点N,由AB∥CD,A1,A2为AB的两个三等分点,点C1,C2为CD的两个三等分点,可得四边形A1CC1A2,四边形A2C1C2B为平行四边形,所以A1C∥A2C1∥C2B,所以AM∥A1C∥A2C1∥C2B∥DN,因为AA1=A1A2=A2B=CC1=C1C2=C2D,由平行线等分线段定理可知,A1C,A2C1,BC2把AD分成的四条线段的长度相等.规律方法 解决此题的关键是找出平行线等分线段定理的基本条件,找准被一组平行线截得的线段.跟踪演练1 如图①,AB∥CD∥EF,且AO=OD=DF,OE=6,则BC=( )A.3 B.6 C.9 D.4
解析 如图②,过O作一直线与AB,CD,EF平行,因为AO=OD=DF,由平行线等分线段定理知,BO=OC=CE,又OE=6,所以BC=6.
答案 B要点二 平行线等分线段定理的推论
例2 如图所示,在△ABC中,∠ACB=90°,AC=BC,E,F分别在AC,BC上,且CE=CF,EM⊥AF交AB于M,CN⊥AF交AB于N.
求证:MN=NB.规律方法 证明同一直线上相邻两条线段相等,常用方法构造三角形及中位线.证明 过M点作ME∥BC,交AB于点E.∵∠ABC=90°,
∴∠AEM=90°,即ME⊥AB.
∵在梯形ABCD中,M是CD的中点,∴AE=EB.
∴ME是AB的垂直平分线.
∴AM=BM.要点三 平行线等分线段定理的综合应用
例3 已知平面α,β,γ,α∥β∥γ,直线l1分别交α,β,γ于A,B,C三点,直线l2分别交α,β,γ于D,E,F三点,且AB=BC.
求证:DE=EF.证明 (1)当l1与l2共面时,由面面平行的性质得AD∥BE∥CF,又∵AB=BC,由平行线等分线段定理得:DE=EF,规律方法 这是平行线等分线段定理在空间的推广,即:如果一组平行平面在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.1.(1)定理中的“一组平行线”是指“平行线组”,是由三条或三条以上互相平行的直线组成的.
(2)定理中的条件“在一条直线上截得的线段相等”实质是指“平行线组”中每相邻两条平行线间的距离都相等.
(3)定理及推论的主要作用在于证明同一直线上的线段相等问题.2.在梯形中,如果已知一腰的中点,添加辅助线的方法
(1)过这一点作底边的平行线,由平行线等分线段定理的推论得另一腰的中点;
(2)可通过延长线段构造全等三角形或相似三角形.
3.在几何证明中添加辅助线的方法
(1)在三角形中,由角平分线可构造全等或相似三角形;
(2)在三角形或梯形中,若有一边上的中点,则过这点可作辅助线.解析 由平行线等分线段定理知CE=ED.
答案 C答案 C3.下列结论正确的是________.(1)如图(1)所示,若l1∥l2∥l3且A1B1=B1C1,则A2B2=B2C2.
(2)如图(2)所示,若l1∥l2∥l3且A1B1=B1C1,则A2B2=B2C2.
(3)如图(3)所示,若l1∥l2∥l3且A1B1=B1C1,则A2B2=B2C2.
解析 由平行线等分线段定理知:(1)(2)(3)都正确.
答案 (1),(2),(3)
2.能独立证明平行线等分线段定理的推论1、推论2.
3.能应用定理和推论解决相关的几何计算问题和证明问题.[知识链接]1.三角形、梯形的中位线定理的内容是什么?
提示 (1)三角形中位线平行于第三边,并且等于它的一半.
(2)梯形的中位线平行于两底,并且等于两底和的一半.提示 BG AC DC[预习导引]1.平行线等分线段定理相等相等A′B′=B′C′2.推论1平行平分3.推论2平行平分要点一 平行线等分线段定理
例1 如图①,在AD两旁作AB∥CD,且AB=CD,A1,A2为AB的两个三等分点,C1,C2为CD的两个三等分点,连接A1C,A2C1,BC2,求证把AD分成四条线段的长度相等.证明 如图②,过点A作直线AM平行于A1C,延长DC交AM于点M,过点D作直线DN平行于BC2,延长AB交DN于点N,由AB∥CD,A1,A2为AB的两个三等分点,点C1,C2为CD的两个三等分点,可得四边形A1CC1A2,四边形A2C1C2B为平行四边形,所以A1C∥A2C1∥C2B,所以AM∥A1C∥A2C1∥C2B∥DN,因为AA1=A1A2=A2B=CC1=C1C2=C2D,由平行线等分线段定理可知,A1C,A2C1,BC2把AD分成的四条线段的长度相等.规律方法 解决此题的关键是找出平行线等分线段定理的基本条件,找准被一组平行线截得的线段.跟踪演练1 如图①,AB∥CD∥EF,且AO=OD=DF,OE=6,则BC=( )A.3 B.6 C.9 D.4
解析 如图②,过O作一直线与AB,CD,EF平行,因为AO=OD=DF,由平行线等分线段定理知,BO=OC=CE,又OE=6,所以BC=6.
答案 B要点二 平行线等分线段定理的推论
例2 如图所示,在△ABC中,∠ACB=90°,AC=BC,E,F分别在AC,BC上,且CE=CF,EM⊥AF交AB于M,CN⊥AF交AB于N.
求证:MN=NB.规律方法 证明同一直线上相邻两条线段相等,常用方法构造三角形及中位线.证明 过M点作ME∥BC,交AB于点E.∵∠ABC=90°,
∴∠AEM=90°,即ME⊥AB.
∵在梯形ABCD中,M是CD的中点,∴AE=EB.
∴ME是AB的垂直平分线.
∴AM=BM.要点三 平行线等分线段定理的综合应用
例3 已知平面α,β,γ,α∥β∥γ,直线l1分别交α,β,γ于A,B,C三点,直线l2分别交α,β,γ于D,E,F三点,且AB=BC.
求证:DE=EF.证明 (1)当l1与l2共面时,由面面平行的性质得AD∥BE∥CF,又∵AB=BC,由平行线等分线段定理得:DE=EF,规律方法 这是平行线等分线段定理在空间的推广,即:如果一组平行平面在一条直线上截得的线段相等,那么在其他直线上截得的线段也相等.1.(1)定理中的“一组平行线”是指“平行线组”,是由三条或三条以上互相平行的直线组成的.
(2)定理中的条件“在一条直线上截得的线段相等”实质是指“平行线组”中每相邻两条平行线间的距离都相等.
(3)定理及推论的主要作用在于证明同一直线上的线段相等问题.2.在梯形中,如果已知一腰的中点,添加辅助线的方法
(1)过这一点作底边的平行线,由平行线等分线段定理的推论得另一腰的中点;
(2)可通过延长线段构造全等三角形或相似三角形.
3.在几何证明中添加辅助线的方法
(1)在三角形中,由角平分线可构造全等或相似三角形;
(2)在三角形或梯形中,若有一边上的中点,则过这点可作辅助线.解析 由平行线等分线段定理知CE=ED.
答案 C答案 C3.下列结论正确的是________.(1)如图(1)所示,若l1∥l2∥l3且A1B1=B1C1,则A2B2=B2C2.
(2)如图(2)所示,若l1∥l2∥l3且A1B1=B1C1,则A2B2=B2C2.
(3)如图(3)所示,若l1∥l2∥l3且A1B1=B1C1,则A2B2=B2C2.
解析 由平行线等分线段定理知:(1)(2)(3)都正确.
答案 (1),(2),(3)
