第1讲 3 相似三角形的判定及性质
文档属性
| 名称 | 第1讲 3 相似三角形的判定及性质 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 12:28:15 | ||
图片预览










文档简介
课件31张PPT。三 相似三角形的判定及性质[学习目标]1.理解相似三角形的定义.
2.理解预备定理的本质.
3.会证明判定定理1,2,3,理解这些定理的内容,能应用这些定理证明相关的几何问题.
4.掌握直角三角形相似的判定定理,会应用定理证明相关的几何问题.[知识链接]1.在初中我们学习过相似三角形,想一想,相似三角形及相似比是如何定义的?
提示 对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似系数).2.判断下列各命题的正确性,正确的打“√”,错误的打“×”
(1)两个等边三角形相似( )
(2)两个直角三角形相似( )
(3)两个等腰直角三角形相似( )
(4)有一个角为50°的两个等腰三角形相似( )
(5)有一个角为100°的两个等腰三角形相似( )√√√××[预习导引]1.相似三角形
(1)定义:对应角相等,对应边成比例的两个三角形叫作相似三角形,相似三角形对应边的比值叫作相似比(或相似系数).
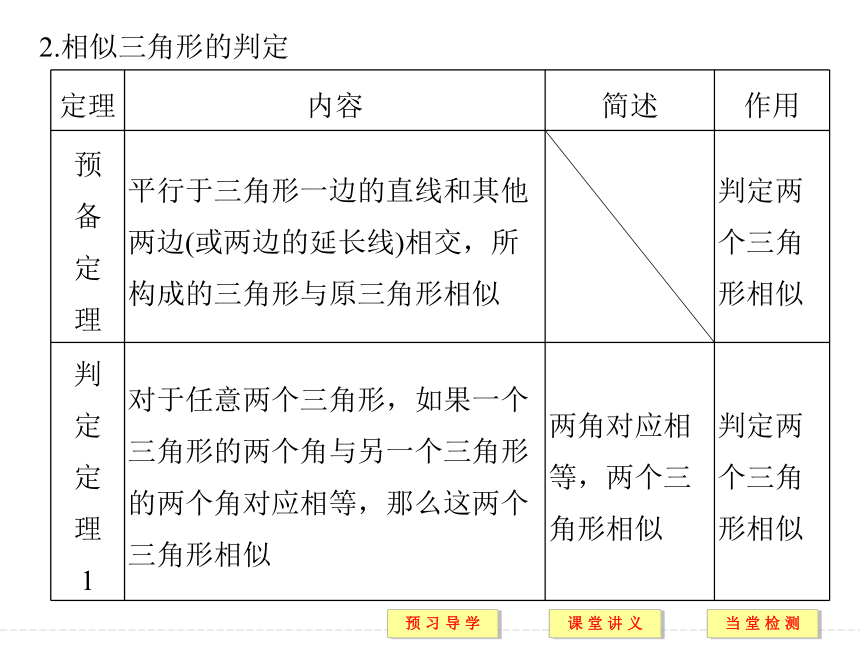
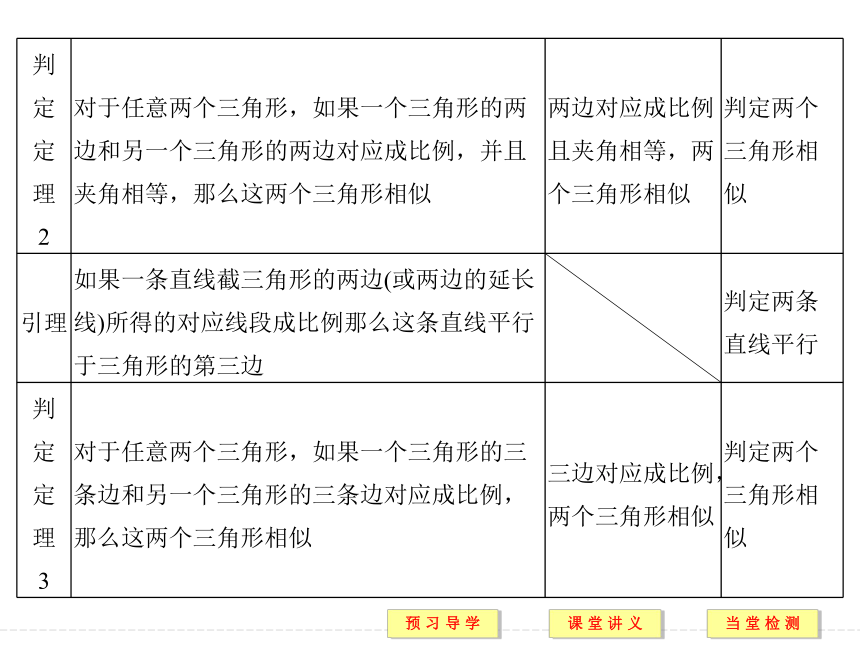
(2)记法:两个三角形相似,用符号“∽”表示,例如△ABC与△A′B′C′相似,记作△ABC∽△A′B′C′.2.相似三角形的判定3.直角三角形相似的判定定理
(1)如果两个直角三角形有一个锐角对应相等,那么它们相似.
(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似.
(3)如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.4.相似三角形的性质定理
(1)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
(2)相似三角形周长的比等于相似比.
(3)相似三角形面积的比等于相似比的平方.5.两个相似三角形外接(内切)圆的直径比、周长比、面积比与相似比的关系
相似三角形外接(内切)圆的直径比、周长比等于相似比,外接(内切)圆的面积比等于相似比的平方.
6.相似三角形的性质和全等三角形的性质比较规律方法 解决此类问题,重点应放在“对应关系”上,根据“对应关系”进行合理的讨论是解题的关键.规律方法 直角三角形相似的判定方法很多,既可根据一般三角形相似的判定方法,又有其独特的判定方法,在求证、识别的过程中可由已知条件结合图形特征,确定合适的方法.规律方法 在利用相似三角形的性质建立比例式时,一定要注意比的顺序,才能得出正确的结果.1.相似三角形判定定理的作用
(1)可以用来判定两个三角形相似;
(2)间接证明角相等,线段长成比例;
(3)为计算线段的长度及角的大小创造条件.
2.三角形相似的判定定理的一些常见推论
推论1:顶角或底角相等的两个等腰三角形相似;
推论2:腰和底对应成比例的两个等腰三角形相似; 推论3:如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似.
推论4:如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似.
3.相似三角形的性质定理的内容归纳起来主要有两个方面:一是相似三角形的对应线段(高、中线、角平分线以及周长)的比等于相似比;二是相似三角形面积的比等于相似比的平方,运用性质定理,拓宽思路,可以探讨得到:两个相似三角形中的所有对应图形(所有对应线段如等分线段,等分角线以及外接圆与内切圆的直径、周长、面积等)与相似比都有一定的关系.解析 在△ABF中,DG∥BF,则△ADG∽△ABF.
答案 B解析 图中Rt△CBA,Rt△CAD,Rt△ABD,Rt△DBE均与Rt△ADE相似.
答案 D
2.理解预备定理的本质.
3.会证明判定定理1,2,3,理解这些定理的内容,能应用这些定理证明相关的几何问题.
4.掌握直角三角形相似的判定定理,会应用定理证明相关的几何问题.[知识链接]1.在初中我们学习过相似三角形,想一想,相似三角形及相似比是如何定义的?
提示 对应角相等,对应边成比例的两个三角形叫做相似三角形.相似三角形对应边的比值叫做相似比(或相似系数).2.判断下列各命题的正确性,正确的打“√”,错误的打“×”
(1)两个等边三角形相似( )
(2)两个直角三角形相似( )
(3)两个等腰直角三角形相似( )
(4)有一个角为50°的两个等腰三角形相似( )
(5)有一个角为100°的两个等腰三角形相似( )√√√××[预习导引]1.相似三角形
(1)定义:对应角相等,对应边成比例的两个三角形叫作相似三角形,相似三角形对应边的比值叫作相似比(或相似系数).
(2)记法:两个三角形相似,用符号“∽”表示,例如△ABC与△A′B′C′相似,记作△ABC∽△A′B′C′.2.相似三角形的判定3.直角三角形相似的判定定理
(1)如果两个直角三角形有一个锐角对应相等,那么它们相似.
(2)如果两个直角三角形的两条直角边对应成比例,那么它们相似.
(3)如果一个直角三角形的斜边和一条直角边与另一个三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.4.相似三角形的性质定理
(1)相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比.
(2)相似三角形周长的比等于相似比.
(3)相似三角形面积的比等于相似比的平方.5.两个相似三角形外接(内切)圆的直径比、周长比、面积比与相似比的关系
相似三角形外接(内切)圆的直径比、周长比等于相似比,外接(内切)圆的面积比等于相似比的平方.
6.相似三角形的性质和全等三角形的性质比较规律方法 解决此类问题,重点应放在“对应关系”上,根据“对应关系”进行合理的讨论是解题的关键.规律方法 直角三角形相似的判定方法很多,既可根据一般三角形相似的判定方法,又有其独特的判定方法,在求证、识别的过程中可由已知条件结合图形特征,确定合适的方法.规律方法 在利用相似三角形的性质建立比例式时,一定要注意比的顺序,才能得出正确的结果.1.相似三角形判定定理的作用
(1)可以用来判定两个三角形相似;
(2)间接证明角相等,线段长成比例;
(3)为计算线段的长度及角的大小创造条件.
2.三角形相似的判定定理的一些常见推论
推论1:顶角或底角相等的两个等腰三角形相似;
推论2:腰和底对应成比例的两个等腰三角形相似; 推论3:如果一个三角形的两边和其中一边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似.
推论4:如果一个三角形的两边和第三边上的中线与另一个三角形的对应部分成比例,那么这两个三角形相似.
3.相似三角形的性质定理的内容归纳起来主要有两个方面:一是相似三角形的对应线段(高、中线、角平分线以及周长)的比等于相似比;二是相似三角形面积的比等于相似比的平方,运用性质定理,拓宽思路,可以探讨得到:两个相似三角形中的所有对应图形(所有对应线段如等分线段,等分角线以及外接圆与内切圆的直径、周长、面积等)与相似比都有一定的关系.解析 在△ABF中,DG∥BF,则△ADG∽△ABF.
答案 B解析 图中Rt△CBA,Rt△CAD,Rt△ABD,Rt△DBE均与Rt△ADE相似.
答案 D
