第2讲 2 圆内接四边形的性质与判定定理
文档属性
| 名称 | 第2讲 2 圆内接四边形的性质与判定定理 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 12:30:48 | ||
图片预览







文档简介
课件26张PPT。二 圆内接四边形的性质与判定定理[学习目标]1.理解圆内接四边形的两条性质定理,并能应用定理解决相关的几何问题.
2.理解圆内接四边形判定定理及推论,能应用定理及推论解决相关的几何问题.[知识链接]1.判断下列各命题是否正确.
(1)任意三角形都有一个外接圆,但可能不止一个;
(2)矩形有唯一的外接圆;
(3)菱形有外接圆;
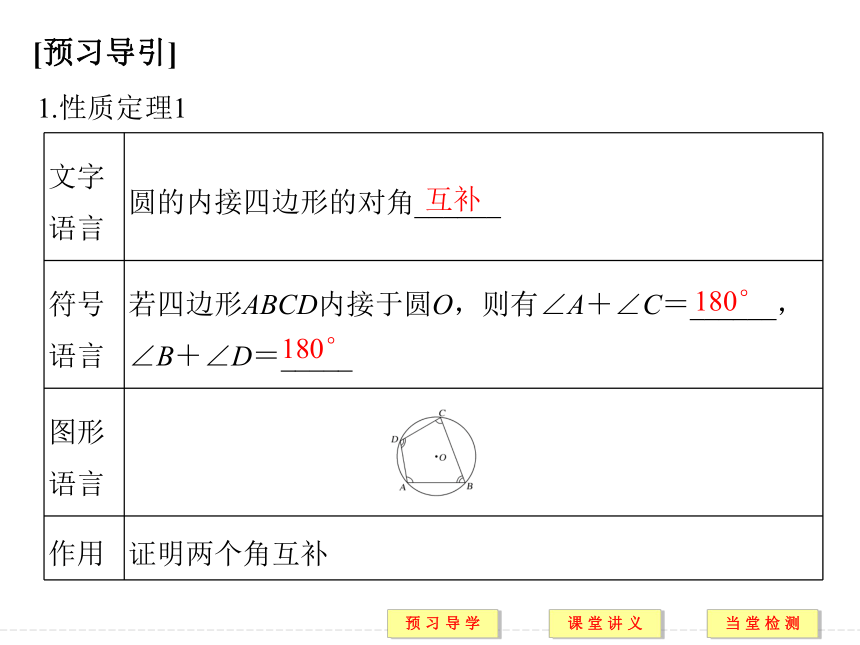
(4)正多边形有外接圆.提示 (1)错误,任意三角形有唯一的外接圆;(2)正确,因为矩形对角线的交点到各顶点的距离相等;(3)错误,只有当菱形是正方形时才有外接圆;(4)正确,因为正多边形的中心到各顶点的距离相等.[预习导引]1.性质定理1互补180°180°2.性质定理2它的内角的对角∠ADC3.圆内接四边形判定定理互补180°180°4.判定定理的推论四个顶点共圆A,B,C,D四点共圆规律方法 1.在本题的证明过程中,都是利用角相等证明了两直线平行,然后利用直线平行,得到比例式相等.
2.圆内接四边形的性质如对角互补,一个外角等于其内对角,可用来作为三角形相似或两直线平行的条件,从而证明一些比例式成立或证明某些等量关系.规律方法 1.本题证明的关键是如何使用点E、D、F是中点这一条件.
2.要判定四点共圆,多借助四边形的对角互补或外角与内对角的关系进行证明.规律方法 1.在解答本题时用到了圆内接四边形的性质,垂径定理等知识,综合性较强.
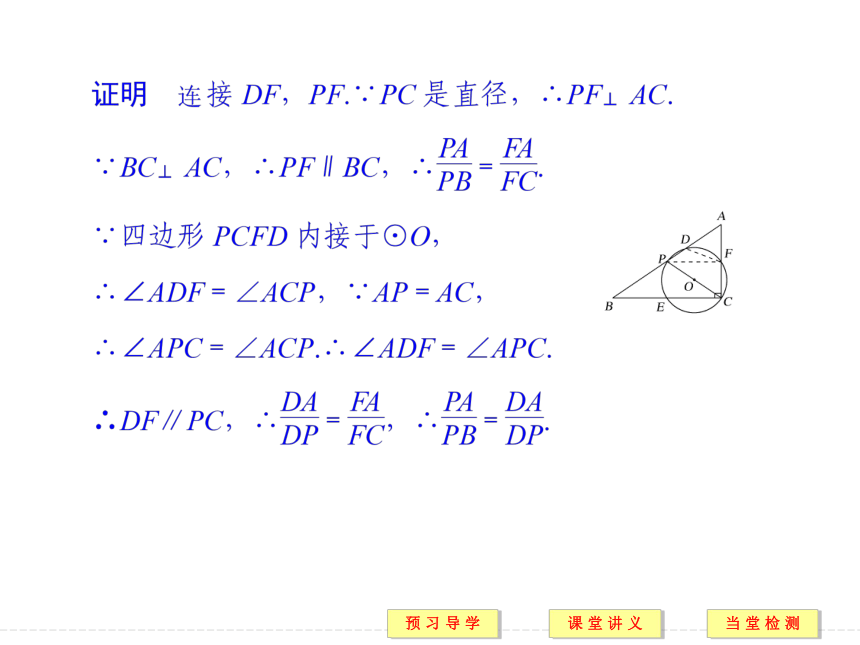
2.此类问题考查知识较为丰富,往往涉及圆内接四边形的判定与性质的证明和应用,最终得到某些结论的成立.证明 由题意知四边形ABFE是圆内接四边形,
∴∠A+∠BFE=180°.又在?ABCD中,AB∥CD,
∴∠A+∠D=180°,∴∠BFE=∠D,
∴E,F,C,D四点共圆.1.对圆内接四边形的理解
(1)圆内接四边形是圆内接多边形的一种特殊情况,它们的关系可以用集合形式表示:{圆内接四边形}?{圆内接多边形}.
(2)掌握一些常见的结论,例如,正多边形一定存在外接圆;三角形一定存在外接圆,并且三角形的外接圆的圆心(即外心)是三条边的垂直平分线的交点;圆内接梯形一定是等腰梯形等.2.判断四点共圆的基本方法
(1)如果四个点与一定点的距离相等,那么这四个点共圆;
(2)如果一个四边形的一组对角互补,那么这个四边形的四个顶点共圆;
(3)如果一个四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆;
(4)如果两个三角形有公共边,公共边所对的角相等且在公共边的同侧,那么这两个三角形的四个顶点共圆.1.下列说法正确的个数有( )①平行四边形内接于圆;②梯形内接于圆;③菱形内接于圆;④矩形内接于圆;⑤正方形内接于圆.
A.1个 B.2个
C.3个 D.4个
解析 根据圆内接四边形的判定定理知,④⑤正确.
答案 B
2.四边形ABCD内接于圆O,∠A=25°,则∠C等于( )
A.25° B.75° C.115° D.155°
解析 ∵四边形ABCD内接于圆O,∴∠A+∠C=180°.又∠A=25°,∴∠C=180°-∠A=155°.
答案 D解析 ∵∠A=50°,∠P=30°,
∴∠QDC=∠A+∠P=80°.又∠QCD=∠A=50°,∴∠Q=180°-80°-50°=50°.
答案 50°
2.理解圆内接四边形判定定理及推论,能应用定理及推论解决相关的几何问题.[知识链接]1.判断下列各命题是否正确.
(1)任意三角形都有一个外接圆,但可能不止一个;
(2)矩形有唯一的外接圆;
(3)菱形有外接圆;
(4)正多边形有外接圆.提示 (1)错误,任意三角形有唯一的外接圆;(2)正确,因为矩形对角线的交点到各顶点的距离相等;(3)错误,只有当菱形是正方形时才有外接圆;(4)正确,因为正多边形的中心到各顶点的距离相等.[预习导引]1.性质定理1互补180°180°2.性质定理2它的内角的对角∠ADC3.圆内接四边形判定定理互补180°180°4.判定定理的推论四个顶点共圆A,B,C,D四点共圆规律方法 1.在本题的证明过程中,都是利用角相等证明了两直线平行,然后利用直线平行,得到比例式相等.
2.圆内接四边形的性质如对角互补,一个外角等于其内对角,可用来作为三角形相似或两直线平行的条件,从而证明一些比例式成立或证明某些等量关系.规律方法 1.本题证明的关键是如何使用点E、D、F是中点这一条件.
2.要判定四点共圆,多借助四边形的对角互补或外角与内对角的关系进行证明.规律方法 1.在解答本题时用到了圆内接四边形的性质,垂径定理等知识,综合性较强.
2.此类问题考查知识较为丰富,往往涉及圆内接四边形的判定与性质的证明和应用,最终得到某些结论的成立.证明 由题意知四边形ABFE是圆内接四边形,
∴∠A+∠BFE=180°.又在?ABCD中,AB∥CD,
∴∠A+∠D=180°,∴∠BFE=∠D,
∴E,F,C,D四点共圆.1.对圆内接四边形的理解
(1)圆内接四边形是圆内接多边形的一种特殊情况,它们的关系可以用集合形式表示:{圆内接四边形}?{圆内接多边形}.
(2)掌握一些常见的结论,例如,正多边形一定存在外接圆;三角形一定存在外接圆,并且三角形的外接圆的圆心(即外心)是三条边的垂直平分线的交点;圆内接梯形一定是等腰梯形等.2.判断四点共圆的基本方法
(1)如果四个点与一定点的距离相等,那么这四个点共圆;
(2)如果一个四边形的一组对角互补,那么这个四边形的四个顶点共圆;
(3)如果一个四边形的一个外角等于它的内对角,那么这个四边形的四个顶点共圆;
(4)如果两个三角形有公共边,公共边所对的角相等且在公共边的同侧,那么这两个三角形的四个顶点共圆.1.下列说法正确的个数有( )①平行四边形内接于圆;②梯形内接于圆;③菱形内接于圆;④矩形内接于圆;⑤正方形内接于圆.
A.1个 B.2个
C.3个 D.4个
解析 根据圆内接四边形的判定定理知,④⑤正确.
答案 B
2.四边形ABCD内接于圆O,∠A=25°,则∠C等于( )
A.25° B.75° C.115° D.155°
解析 ∵四边形ABCD内接于圆O,∴∠A+∠C=180°.又∠A=25°,∴∠C=180°-∠A=155°.
答案 D解析 ∵∠A=50°,∠P=30°,
∴∠QDC=∠A+∠P=80°.又∠QCD=∠A=50°,∴∠Q=180°-80°-50°=50°.
答案 50°
