第2讲 3 圆的切线的性质及判定定理
文档属性
| 名称 | 第2讲 3 圆的切线的性质及判定定理 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 00:00:00 | ||
图片预览






文档简介
课件27张PPT。三 圆的切线的性质及判定定理[学习目标]1.理解切线的性质定理、判定定理及两个推论,能应用定理及推论解决相关的几何问题.
2.能归纳并正确表示由圆的切线性质定理和两个推论整合而成的定理.[知识链接]1.根据直线与圆公共点的个数,说明它们有怎样的位置关系?
提示 直线与圆有两个公共点时,直线与圆相交;直线与圆有一个公共点时,直线与圆相切;直线与圆没有公共点时,直线与圆相离.(1)与圆有公共点的直线是圆的切线;
(2)垂直于圆的半径的直线是圆的切线;
(3)与圆心的距离等于半径的直线是圆的切线;
(4)过直径的端点,垂直于此直径的直线是圆的切线.
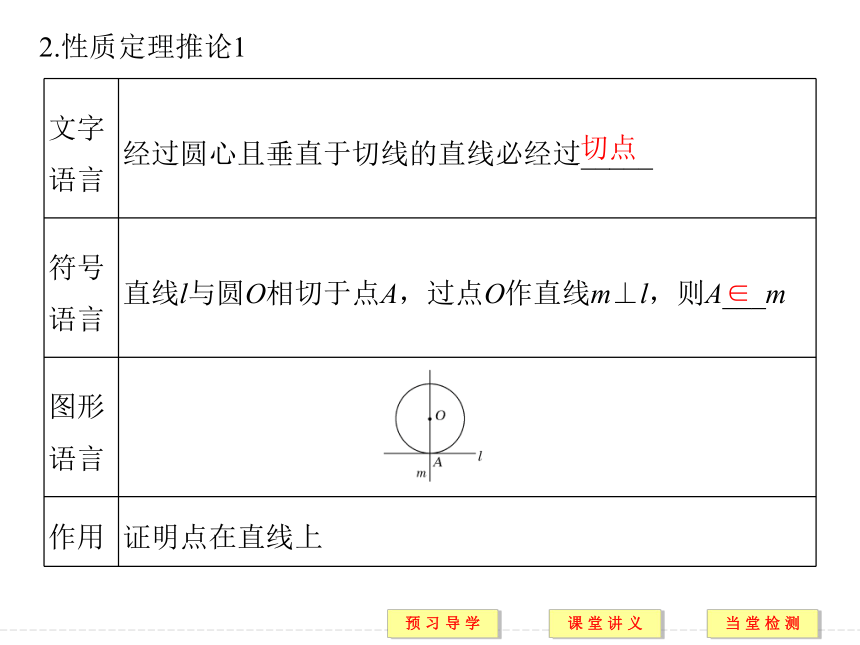
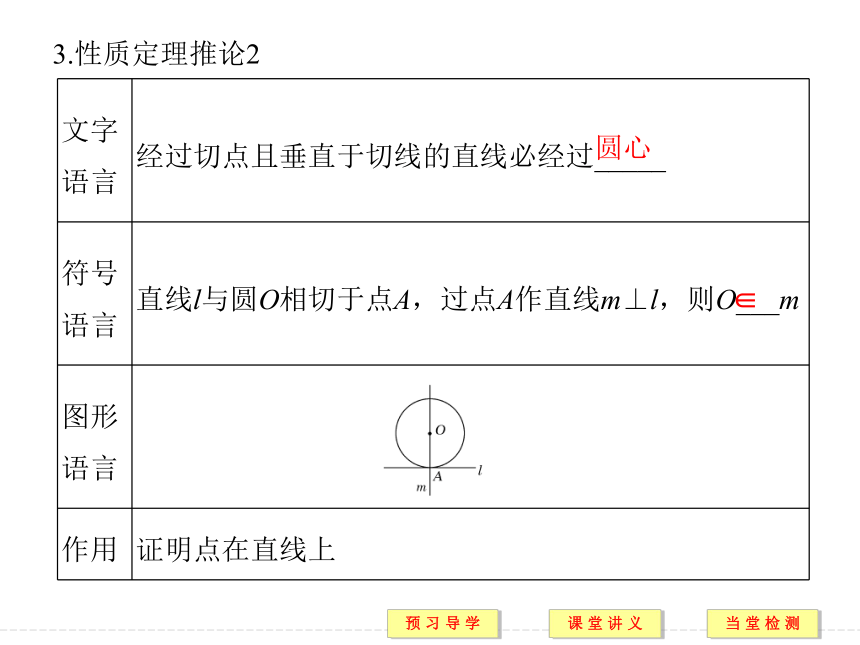
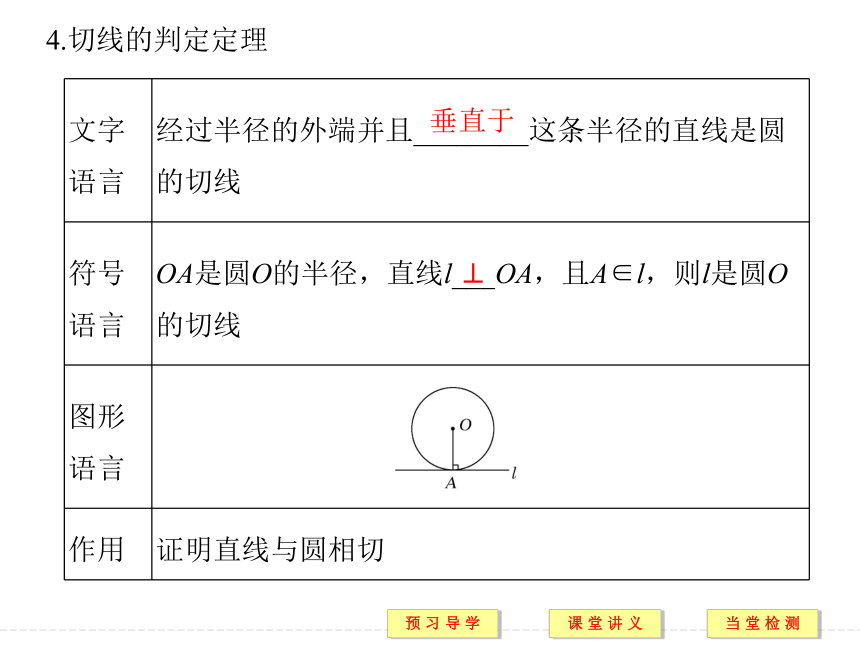
提示 (3)(4)正确.2.下列关于切线的说法中,正确的有哪些?[预习导引]1.切线的性质定理垂直于⊥2.性质定理推论1切点∈3.性质定理推论2圆心∈4.切线的判定定理垂直于⊥规律方法 1.本例中第(2)小题是通过三角形相似来寻找AD、AC与AB之间关系的.
2.利用圆的切线的性质来证明或进行有关的计算,有时需添加辅助线,其中连接圆心和切点的半径是常用辅助线.从而可以构造直角三角形,利用直角三角形边角关系求解,或利用勾股定理求解,或利用三角形相似求解等.要点二 圆的切线的判定
例2 已知:AB是⊙O的直径,BC是⊙O的切线,切点为B,过点A作AD∥OC,交⊙O于点D.
求证:DC是⊙O的切线.规律方法 判断一条直线是圆的切线时,常用辅助线的作法:
(1)如果已知这条直线与圆有公共点,则连接圆心与这个公共点,设法证明连接所得到的半径与这条直线垂直,简记为“连半径,证垂直”;
(2)若题目未说明这条直线与圆有公共点,则过圆心作这条直线的垂线,得垂线段,再证明这条垂线段的长等于半径,简记“作垂直,证半径”.规律方法 对圆的切线的性质与判定的综合考查往往是热点,其解答思路常常是先证明某直线是圆的切线,再利用切线的性质来求解相关结果.1.圆的切线的判定方法有
(1)定义法:和圆只有一个公共点的直线是圆的切线;
(2)几何法:和圆心距离等于半径的直线是圆的切线;
(3)判定定理:过半径外端点且与这条半径垂直的直线是圆的切线.
2.圆的切线的性质与判定的综合运用
在解决有关圆的切线问题,添加辅助线有以下规律:(1)已知一条直线是圆的切线时,通常连接圆心和切点,这条半径垂直于切线.
(2)要证明某条直线是圆的切线时,若已知直线经过圆上的某一点,则需作出经过这一点的半径,证明直线垂直于这条半径,简记为“连半径,证垂直”;若直线与圆的公共点没有确定,则应过圆心作直线的垂线,得到垂线段,再证明这条垂线段的长等于半径,简记为“作垂直,证半径”.解析 ∵l与⊙O相切,∴l⊥OA.∴OA⊥AB.∴∠OAB=90°,△OAB是直角三角形.
答案 C2.已知AB是⊙O的切线,下列给出的条件中,能判定AB⊥CD的是( )A.AB与⊙O相切于直线CD上的点C
B.CD经过圆心O
C.CD是直线
D.AB与⊙O相切于点C,CD过圆心O解析 由图①②③可知,根据选项A,B,C中的条件都不能判定AB⊥CD;因为圆的切线垂直于经过切点的半径,所以选项D正确(如图④).答案 D3.如图所示,DB,DC是⊙O的两条切线,A是圆上一点,已知∠D=46°,则∠A=________.答案 67°
2.能归纳并正确表示由圆的切线性质定理和两个推论整合而成的定理.[知识链接]1.根据直线与圆公共点的个数,说明它们有怎样的位置关系?
提示 直线与圆有两个公共点时,直线与圆相交;直线与圆有一个公共点时,直线与圆相切;直线与圆没有公共点时,直线与圆相离.(1)与圆有公共点的直线是圆的切线;
(2)垂直于圆的半径的直线是圆的切线;
(3)与圆心的距离等于半径的直线是圆的切线;
(4)过直径的端点,垂直于此直径的直线是圆的切线.
提示 (3)(4)正确.2.下列关于切线的说法中,正确的有哪些?[预习导引]1.切线的性质定理垂直于⊥2.性质定理推论1切点∈3.性质定理推论2圆心∈4.切线的判定定理垂直于⊥规律方法 1.本例中第(2)小题是通过三角形相似来寻找AD、AC与AB之间关系的.
2.利用圆的切线的性质来证明或进行有关的计算,有时需添加辅助线,其中连接圆心和切点的半径是常用辅助线.从而可以构造直角三角形,利用直角三角形边角关系求解,或利用勾股定理求解,或利用三角形相似求解等.要点二 圆的切线的判定
例2 已知:AB是⊙O的直径,BC是⊙O的切线,切点为B,过点A作AD∥OC,交⊙O于点D.
求证:DC是⊙O的切线.规律方法 判断一条直线是圆的切线时,常用辅助线的作法:
(1)如果已知这条直线与圆有公共点,则连接圆心与这个公共点,设法证明连接所得到的半径与这条直线垂直,简记为“连半径,证垂直”;
(2)若题目未说明这条直线与圆有公共点,则过圆心作这条直线的垂线,得垂线段,再证明这条垂线段的长等于半径,简记“作垂直,证半径”.规律方法 对圆的切线的性质与判定的综合考查往往是热点,其解答思路常常是先证明某直线是圆的切线,再利用切线的性质来求解相关结果.1.圆的切线的判定方法有
(1)定义法:和圆只有一个公共点的直线是圆的切线;
(2)几何法:和圆心距离等于半径的直线是圆的切线;
(3)判定定理:过半径外端点且与这条半径垂直的直线是圆的切线.
2.圆的切线的性质与判定的综合运用
在解决有关圆的切线问题,添加辅助线有以下规律:(1)已知一条直线是圆的切线时,通常连接圆心和切点,这条半径垂直于切线.
(2)要证明某条直线是圆的切线时,若已知直线经过圆上的某一点,则需作出经过这一点的半径,证明直线垂直于这条半径,简记为“连半径,证垂直”;若直线与圆的公共点没有确定,则应过圆心作直线的垂线,得到垂线段,再证明这条垂线段的长等于半径,简记为“作垂直,证半径”.解析 ∵l与⊙O相切,∴l⊥OA.∴OA⊥AB.∴∠OAB=90°,△OAB是直角三角形.
答案 C2.已知AB是⊙O的切线,下列给出的条件中,能判定AB⊥CD的是( )A.AB与⊙O相切于直线CD上的点C
B.CD经过圆心O
C.CD是直线
D.AB与⊙O相切于点C,CD过圆心O解析 由图①②③可知,根据选项A,B,C中的条件都不能判定AB⊥CD;因为圆的切线垂直于经过切点的半径,所以选项D正确(如图④).答案 D3.如图所示,DB,DC是⊙O的两条切线,A是圆上一点,已知∠D=46°,则∠A=________.答案 67°
