第2讲 4 弦切角的性质
图片预览







文档简介
课件23张PPT。四 弦切角的性质[学习目标]1.理解弦切角的定义及性质,并能解决与弦切角有关的问题.
2.理解弦切角定理,并能应用定理证明相关的几何问题.[知识链接]1.在前面我们研究过与圆有关的哪两种角?这两种角是如何定义的?
提示 前面我们研究过圆心角和圆周角;顶点在圆心,两边与圆相交的角叫做圆心角,顶点在圆上,两边与圆相交的角叫做圆周角.2.在同圆或等圆中圆心角与圆周角各有什么性质,它们又有怎样的关系?
提示 在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧也相等;相等的弦或相等的弧所对的圆心角相等.同弧所对的圆周角等于圆心角的一半.3.如下图,圆周角∠CAB,让射线AC绕点A旋转,产生无数个圆周角,当AC绕点A旋转至与圆相切时,停止旋转,得∠BAE.这时∠BAE还是圆周角吗?为什么?提示 不是圆周角,因为角的一边与圆相切,只有角的两边都与圆相交时,才是圆周角.[预习导引]1.弦切角
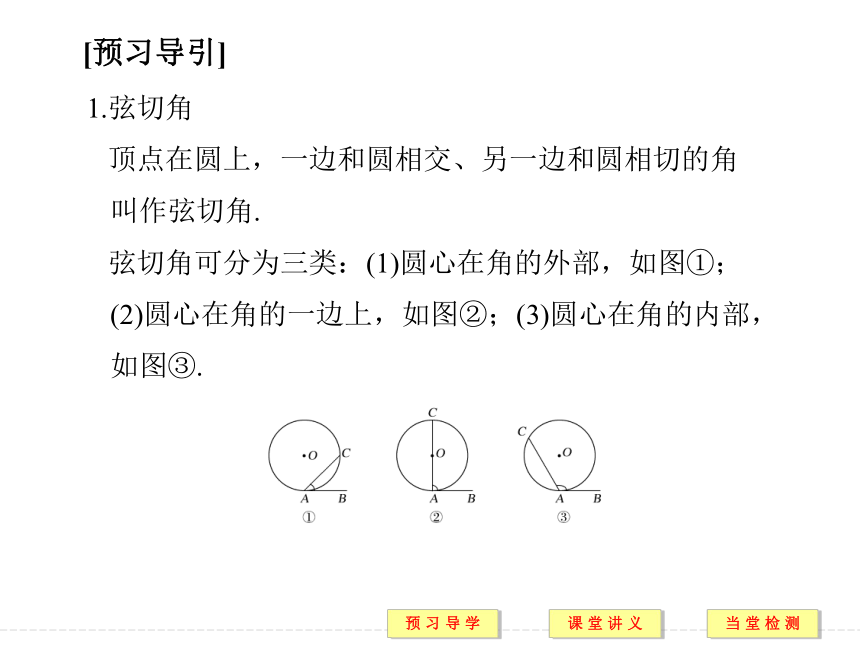
顶点在圆上,一边和圆相交、另一边和圆相切的角叫作弦切角.
弦切角可分为三类:(1)圆心在角的外部,如图①;(2)圆心在角的一边上,如图②;(3)圆心在角的内部,如图③.2.弦切角定理规律方法 1.本题在证明过程中,多次使用了角的转化,而转化的依据是弦切角定理和圆周角定理.
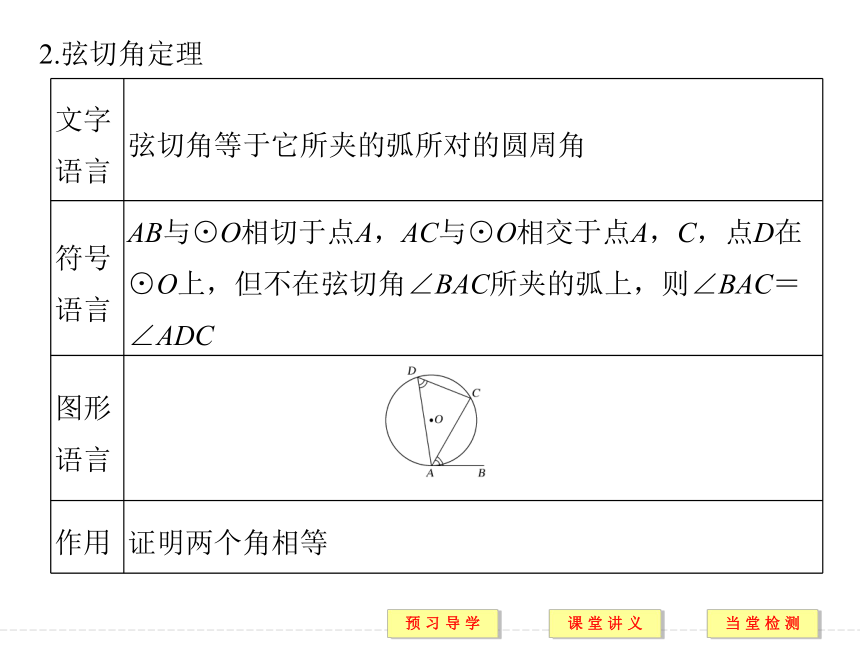
2.利用弦切角定理进行计算、证明,要特别注意弦切角所夹弧所对的圆周角,有时与圆的直径所对的圆周角结合运用,同时要注意根据题目的需要可添加辅助线构成所需要的弦切角.答案 125°规律方法 1.弦切角定理经常作为工具,进行三角形相似的证明,然后利用三角形相似进一步确定相应边之间的关系,在圆中证明比例式或等积式,常常需要借助于三角形相似处理.
2.弦切角定理有时还与圆周角定理等知识综合运用,它们不但在证明方法上相似,在解题功能上也有相似之处,通常都作为辅助工具出现.规律方法 借助于弦切角定理和圆的其他性质(如等弧所对的弦相等)以及三角形有关知识我们可以得到特殊三角形或全等三角形,从而证得线段相等.(1)弦切角定理的推论:若一个圆的两个弦切角所夹的弧相等,则这两个弦切角也相等.
(2)弦切角定理也可以表述为弦切角的度数等于它所夹的弧的度数的一半,这就建立了弦切角与弧之间的数量关系,它为直接依据弧进行角的转换确立了基础.(3)圆心角、圆周角、弦切角的比较.解析 ∠ADB是圆周角,∠AOB是圆心角,∠ABC是弦切角,∠BAO不是弦切角.
答案 C解析 ∵∠NMP是弦切角,∴∠NMP=∠PQM=70°.
答案 B3.已知AB切⊙O于A点,圆周被AC所分成的优弧与劣弧之比为3∶1,则夹劣弧的弦切角∠BAC=________.解析 ∵优弧与劣弧之比为3∶1,∴劣弧所对的圆心角为90°,所对的圆周角为45°,故由弦切角定理可知,弦切角∠BAC=45°.
答案 45°证明 ∵PE切⊙O于点E,
∴∠BEP=∠A,
∵PC平分∠APE,∴∠3=∠4,
又∵∠1=∠3+∠A,∠2=∠4+∠BEP,
∴∠1=∠2,∴EC=ED.
2.理解弦切角定理,并能应用定理证明相关的几何问题.[知识链接]1.在前面我们研究过与圆有关的哪两种角?这两种角是如何定义的?
提示 前面我们研究过圆心角和圆周角;顶点在圆心,两边与圆相交的角叫做圆心角,顶点在圆上,两边与圆相交的角叫做圆周角.2.在同圆或等圆中圆心角与圆周角各有什么性质,它们又有怎样的关系?
提示 在同圆或等圆中,相等的圆心角所对的弦相等,所对的弧也相等;相等的弦或相等的弧所对的圆心角相等.同弧所对的圆周角等于圆心角的一半.3.如下图,圆周角∠CAB,让射线AC绕点A旋转,产生无数个圆周角,当AC绕点A旋转至与圆相切时,停止旋转,得∠BAE.这时∠BAE还是圆周角吗?为什么?提示 不是圆周角,因为角的一边与圆相切,只有角的两边都与圆相交时,才是圆周角.[预习导引]1.弦切角
顶点在圆上,一边和圆相交、另一边和圆相切的角叫作弦切角.
弦切角可分为三类:(1)圆心在角的外部,如图①;(2)圆心在角的一边上,如图②;(3)圆心在角的内部,如图③.2.弦切角定理规律方法 1.本题在证明过程中,多次使用了角的转化,而转化的依据是弦切角定理和圆周角定理.
2.利用弦切角定理进行计算、证明,要特别注意弦切角所夹弧所对的圆周角,有时与圆的直径所对的圆周角结合运用,同时要注意根据题目的需要可添加辅助线构成所需要的弦切角.答案 125°规律方法 1.弦切角定理经常作为工具,进行三角形相似的证明,然后利用三角形相似进一步确定相应边之间的关系,在圆中证明比例式或等积式,常常需要借助于三角形相似处理.
2.弦切角定理有时还与圆周角定理等知识综合运用,它们不但在证明方法上相似,在解题功能上也有相似之处,通常都作为辅助工具出现.规律方法 借助于弦切角定理和圆的其他性质(如等弧所对的弦相等)以及三角形有关知识我们可以得到特殊三角形或全等三角形,从而证得线段相等.(1)弦切角定理的推论:若一个圆的两个弦切角所夹的弧相等,则这两个弦切角也相等.
(2)弦切角定理也可以表述为弦切角的度数等于它所夹的弧的度数的一半,这就建立了弦切角与弧之间的数量关系,它为直接依据弧进行角的转换确立了基础.(3)圆心角、圆周角、弦切角的比较.解析 ∠ADB是圆周角,∠AOB是圆心角,∠ABC是弦切角,∠BAO不是弦切角.
答案 C解析 ∵∠NMP是弦切角,∴∠NMP=∠PQM=70°.
答案 B3.已知AB切⊙O于A点,圆周被AC所分成的优弧与劣弧之比为3∶1,则夹劣弧的弦切角∠BAC=________.解析 ∵优弧与劣弧之比为3∶1,∴劣弧所对的圆心角为90°,所对的圆周角为45°,故由弦切角定理可知,弦切角∠BAC=45°.
答案 45°证明 ∵PE切⊙O于点E,
∴∠BEP=∠A,
∵PC平分∠APE,∴∠3=∠4,
又∵∠1=∠3+∠A,∠2=∠4+∠BEP,
∴∠1=∠2,∴EC=ED.
