第2讲 5 与圆有关的比例线段
图片预览










文档简介
课件30张PPT。五 与圆有关的比例线段
[学习目标]1.掌握相交弦定理、割线定理、切割线定理以及切线长定理.
2.能应用这些定理解决与圆有关的比例线段问题.[知识链接] 提示 ∠ACB=90°,由射影定理得:PC2=PA·PB.
2.若CD与AB不垂直,会有怎样的结论?
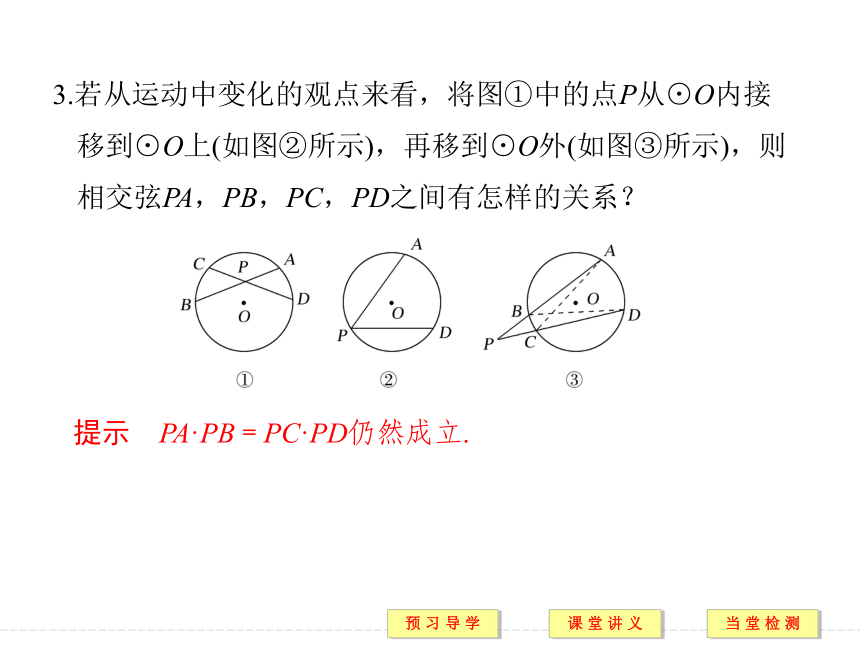
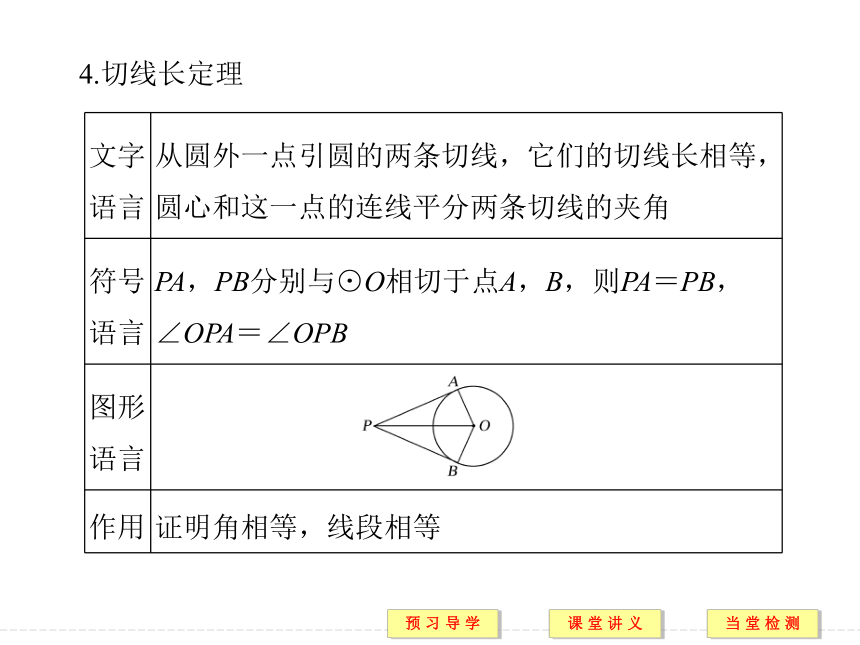
提示 PC·PD=PA·PB.3.若从运动中变化的观点来看,将图①中的点P从⊙O内接移到⊙O上(如图②所示),再移到⊙O外(如图③所示),则相交弦PA,PB,PC,PD之间有怎样的关系?提示 PA·PB=PC·PD仍然成立.[预习导引]1.相交弦定理2.割线定理3.切割线定理4.切线长定理证明 连接PO.
∵P为弦AB的中点,∴OP⊥AB,AP=PB,∵PE⊥OA,
∴在Rt△APO中,AP2=AE·AO,由相交弦定理得PD·PC=PA·PB,∴PD·PC=AP2,
∴PD·PC=AE·AO.规律方法 用相交弦定理解决此类问题的步骤:
(1)结合图形,找准分点及线段被分点所分成的线段;
(2)正确应用相交弦定理列出关系式;相交弦定理的运用多是与垂径定理、射影定理、直角三角形的性质相结合.规律方法 利用切割线定理证明乘积式成立是一种重要的题型,是高考出题的热点之一,在解决此类问题时,要分清切线与割线以及相关图形的特点,结合三角形、四边形等图形的性质加以论证.规律方法 解此题第(2)问时,注意四边形内角和这一隐含条件的使用,当已知条件中有切线时,通常连接切点和圆心,以便使用“垂直”这一结论,这也是切线问题常用的辅助线.答案 101.相交弦定理的证明过程是利用分类讨论思想进行分析的,也可以理解为是由特殊到一般的过程进行分析的.
2.割线定理是圆中的比例线段,在证明割线定理时所用的构造相似三角形的方法十分重要,应注意很好地把握.3.要真正弄懂切割线定理的数量关系,把握定理叙述中的“从”、“引”、“切线长”、“两条线段长”等关键字样.4.(1)切线长定理在证明线段相等、角相等及垂直关系中占有重要地位,故为重点.
(2)“切割线定理”和“切线长定理”实际上是割线定理的特例.
(3)对于定理中涉及到的线段,在相交弦定理和割线定理中,能实现知三求一,在切割线定理中能实现知二求一.
解析 ∵AE·EB=DE·EC,∴2EB=4×1.∴EB=2.
答案 B
解析 ∵PA2=PB·PC=4×9=36,∴PA=6.
答案 B
[学习目标]1.掌握相交弦定理、割线定理、切割线定理以及切线长定理.
2.能应用这些定理解决与圆有关的比例线段问题.[知识链接] 提示 ∠ACB=90°,由射影定理得:PC2=PA·PB.
2.若CD与AB不垂直,会有怎样的结论?
提示 PC·PD=PA·PB.3.若从运动中变化的观点来看,将图①中的点P从⊙O内接移到⊙O上(如图②所示),再移到⊙O外(如图③所示),则相交弦PA,PB,PC,PD之间有怎样的关系?提示 PA·PB=PC·PD仍然成立.[预习导引]1.相交弦定理2.割线定理3.切割线定理4.切线长定理证明 连接PO.
∵P为弦AB的中点,∴OP⊥AB,AP=PB,∵PE⊥OA,
∴在Rt△APO中,AP2=AE·AO,由相交弦定理得PD·PC=PA·PB,∴PD·PC=AP2,
∴PD·PC=AE·AO.规律方法 用相交弦定理解决此类问题的步骤:
(1)结合图形,找准分点及线段被分点所分成的线段;
(2)正确应用相交弦定理列出关系式;相交弦定理的运用多是与垂径定理、射影定理、直角三角形的性质相结合.规律方法 利用切割线定理证明乘积式成立是一种重要的题型,是高考出题的热点之一,在解决此类问题时,要分清切线与割线以及相关图形的特点,结合三角形、四边形等图形的性质加以论证.规律方法 解此题第(2)问时,注意四边形内角和这一隐含条件的使用,当已知条件中有切线时,通常连接切点和圆心,以便使用“垂直”这一结论,这也是切线问题常用的辅助线.答案 101.相交弦定理的证明过程是利用分类讨论思想进行分析的,也可以理解为是由特殊到一般的过程进行分析的.
2.割线定理是圆中的比例线段,在证明割线定理时所用的构造相似三角形的方法十分重要,应注意很好地把握.3.要真正弄懂切割线定理的数量关系,把握定理叙述中的“从”、“引”、“切线长”、“两条线段长”等关键字样.4.(1)切线长定理在证明线段相等、角相等及垂直关系中占有重要地位,故为重点.
(2)“切割线定理”和“切线长定理”实际上是割线定理的特例.
(3)对于定理中涉及到的线段,在相交弦定理和割线定理中,能实现知三求一,在切割线定理中能实现知二求一.
解析 ∵AE·EB=DE·EC,∴2EB=4×1.∴EB=2.
答案 B
解析 ∵PA2=PB·PC=4×9=36,∴PA=6.
答案 B
