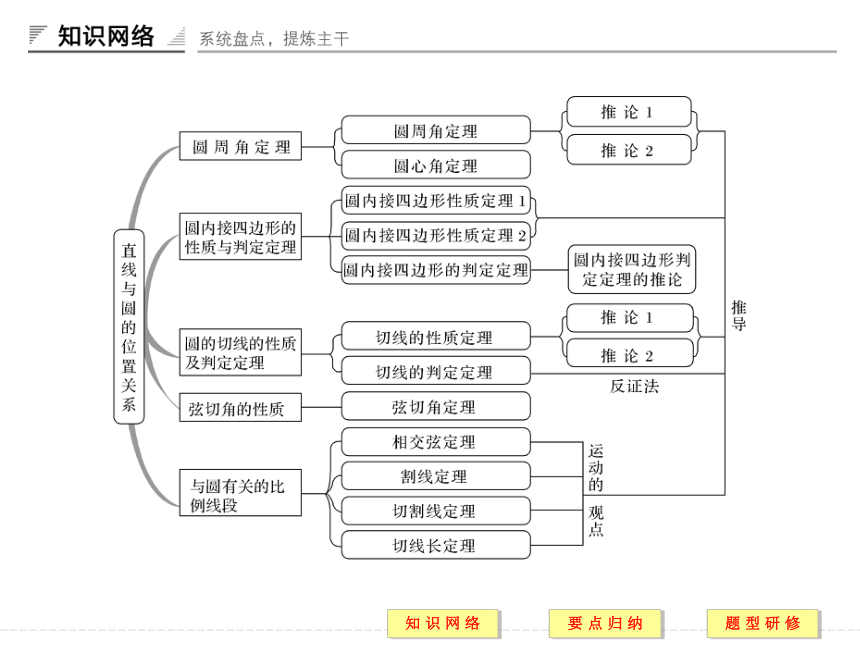
第2讲 直线与圆的位置关系复习
图片预览










文档简介
课件54张PPT。讲末复习1.圆周角定理圆周角定理:圆上一条弦所对的圆周角等于它所对的圆心角的一半,其度数等于它所对的弧的度数的一半.
推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
相交弦所成角定理:圆的两条相交弦所成角的度数等于它所夹的弧与它的对顶角所夹弧的度数和的一半.2.圆内接四边形的性质与判定(1)圆内接四边形的性质
定理1 圆内接四边形对角互补.
定理2 圆内接四边形的外角等于它的内对角.
(2)圆内接四边形的判定
定理 如果一个四边形的一组对角互补,那么这个四边形内接于圆.
推论1 如果四边形的一个外角等于它的内对角,那么这个四边形内接于圆.
推论2 如果两个三角形有一条公共边,这条边所对的角相等,并且在公共边同侧,那么这两个三角形有公共的外接圆.3.圆的切线的性质与判定(1)圆的切线的性质
定理 圆的切线垂直于过切点的半径.
推论1 经过圆心且垂直于切线的直线必过切点.
推论2 经过切点且垂直于切线的直线必过圆心.
(2)圆的切线的判定
定理 经过半径的外端点并且垂直于这条半径的直线是圆的切线.
(3)切线长定理:从圆外一点引圆的两条切线长相等.
推论 经过圆外的一个已知点和圆心的直线,平分从这点向圆所作的两条切线所夹的角.4.弦切角(1)弦切角的概念:顶点在圆上,一边和圆相交,另一边和圆相切的角叫弦切角.
弦切角必须具备三个条件:①顶点在圆上,②一边是圆的切线,③一边是过切点的弦.三者缺一不可.
(2)弦切角定理:弦切角等于它所夹的弧对的圆周角,其度数等于它所夹的弧的度数的一半.
推论 同弧(或等弧)上的弦切角相等;同弧(或等弧)上的弦切角与圆周角相等.5.圆幂定理(1)相交弦定理:圆的两条相交弦,被交点分成的两条线段长的积相等.
推论 如果弦与直径垂直相交,那么弦的一半是它分直
径所成的两条线段的比例中项.
(2)割线定理:从圆外一点引圆的两条割线,这点到每条割线与圆的交点的两条线段长的积相等.(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆的交点的两条线段长的比例中项.
逆定理 从圆外一点引圆的割线,如果圆上一点与这点的连线是这点到割线与圆的交点的两条线段的比例中项,那么这点与圆上点的连线是圆的切线.题型一 分类讨论思想分类讨论是一种逻辑方法,也是一种数学思想.当我们面临的数学问题不能以统一形式解决时,可以把已知条件的范围划分为若干个子集,在各个子集内分别讨论问题的解,然后通过综合各类解而得到原问题的解答,这种解决问题的思想方法叫做分类讨论的思想方法.
应用分类讨论的思想方法解题的一般步骤是:
(1)确定讨论的对象以及被讨论对象的全域;
(2)合理分类,统一标准,不重不漏;
(3)逐段逐类讨论,分级进行;
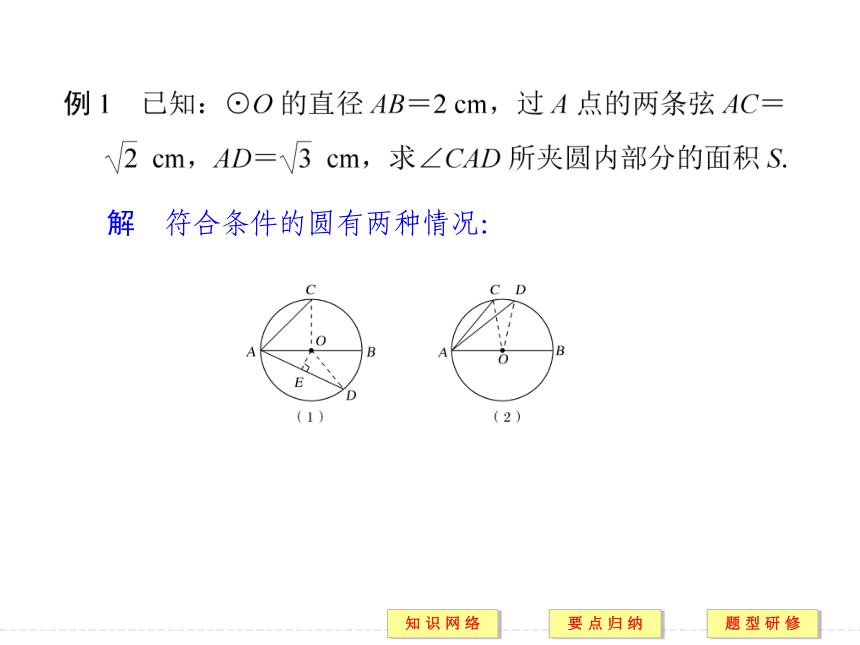
(4)归纳总结,作出整个题目的结论.解 符合条件的圆有两种情况:规律方法 分析所给条件,正确把握C、D两点与直径AB的位置关系,从而确定分类的标准,以避免只考虑AC、AD在直径AB同侧或异侧一种情况.跟踪演练1 已知⊙O1与⊙O2相交于A,B,⊙O1的半径r1=5,⊙O2的半径r2=4,AB=6,求O1O2的长.解 ①若O1,O2在AB的异侧(如图(1)所示),O1O2垂直平分AB,题型二 化归思想
化归思想又称转化思想,是把待解决的问题或难解决的问题,通过某种转化过程,归结为一类已经解决或易解决的问题,最终求得问题的解答.在解决直线与圆的位置的有关问题时,常常需作辅助线,通过作辅助可将圆的问题化归为特殊三角形或四边形的问题,使问题得到解决.(1)证明 ∵∠ADE=∠B+∠BAD,
∠DAE=∠DAC+∠CAE,
又∠BAD=∠DAC,∠B=∠CAE,
∴∠ADE=∠DAE.∴AE=DE.
又DE是半圆的直径,
∴∠DFE=90°,∴AF=DF.规律方法 本题综合性较强,在(1)的证明中,把证明AF=DF的问题转化为证明AE=DE的问题,进而又转化为证明∠DAE=∠ADE的问题;在(2)的解答中,通过作辅助线,把求sin∠AED的问题转化为求sin∠AEG的问题,进而转化为求AG,AE的问题;在(3)的解答中,把求S△ABC的问题转化为求BC与AG的问题,如此等等,每一步都体现着转化与化归的思想方法.题型三 函数方程思想在直线与圆的位置关系中,涉及很多数量关系,既有角的大小,也有线段的长度,在求它们的大小时,有时不太方便,这时我们可以利用相似三角形或有关定理建立以欲求量为未知数的函数或方程,通过求函数的最值或解方程求出所要求的量,这种函数方程的思想在直线与圆的位置关系中有广泛的应用.例3 如图(1)所示,四边形ABCD是半径为1的半圆的内接等腰梯形,其下底是半圆的直径.写出该梯形的周长y与腰长x之间的函数关系式,当腰长为多少时,周长最长?并求出周长的最大值.解 如图(2)所示,过点O作OE⊥DC于点E,过点D作DF⊥AB于点F,连接OD.
设DE=m,OE=n,则DF=n,AF=AO-FO=1-m,且腰长x>0.规律方法 解本题的关键是建立周长y与腰长x之间的函数关系式.过点O作OE⊥DC,E为垂足,过点D作DF⊥AB,F为垂足,这样将四边形中的线段的长度计算问题转化为直角三角形中的边长的计算问题.题型四 数形结合思想数形结合思想是将抽象的数学语言与直观图形结合起来,使抽象思维与形象思维相结合,通过对图形的认识,数与形的转化,化抽象为具体,化难为易,使问题得到解决.规律方法 将计算与具体图形相结合是解决问题的关键,通过分析图形的位置关系,得到数量关系.跟踪演练4 两圆半径分别为4和2,如果它们有两条互相垂直的公切线,求它们的圆心距.体验高考答案 A解析 由切割线定理,知PA2=PC·PD,即62=3PD,解得PD=12,所以CD=PD-PC=9,又因为CE∶ED=2∶1,所以CE=6,ED=3.由相交弦定理,知AE·BE=CE·ED,即9BE=6×3,解得BE=2.
答案 2答案 8答案 5(1)证明 因为DE为⊙O直径,则∠BED+∠EDB=90°,
又BC⊥DE,
所以∠CBD+∠EDB=90°,从而∠CBD=∠BED.
又AB切⊙O于点B,得∠DBA=∠BED,
所以∠CBD=∠DBA.11.如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连结DB并延长交⊙O于点E.证明:
(1)AC·BD=AD·AB;
(2)AC=AE.
推论1 同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧也相等.
推论2 半圆(或直径)所对的圆周角是直角;90°的圆周角所对的弦是直径.
相交弦所成角定理:圆的两条相交弦所成角的度数等于它所夹的弧与它的对顶角所夹弧的度数和的一半.2.圆内接四边形的性质与判定(1)圆内接四边形的性质
定理1 圆内接四边形对角互补.
定理2 圆内接四边形的外角等于它的内对角.
(2)圆内接四边形的判定
定理 如果一个四边形的一组对角互补,那么这个四边形内接于圆.
推论1 如果四边形的一个外角等于它的内对角,那么这个四边形内接于圆.
推论2 如果两个三角形有一条公共边,这条边所对的角相等,并且在公共边同侧,那么这两个三角形有公共的外接圆.3.圆的切线的性质与判定(1)圆的切线的性质
定理 圆的切线垂直于过切点的半径.
推论1 经过圆心且垂直于切线的直线必过切点.
推论2 经过切点且垂直于切线的直线必过圆心.
(2)圆的切线的判定
定理 经过半径的外端点并且垂直于这条半径的直线是圆的切线.
(3)切线长定理:从圆外一点引圆的两条切线长相等.
推论 经过圆外的一个已知点和圆心的直线,平分从这点向圆所作的两条切线所夹的角.4.弦切角(1)弦切角的概念:顶点在圆上,一边和圆相交,另一边和圆相切的角叫弦切角.
弦切角必须具备三个条件:①顶点在圆上,②一边是圆的切线,③一边是过切点的弦.三者缺一不可.
(2)弦切角定理:弦切角等于它所夹的弧对的圆周角,其度数等于它所夹的弧的度数的一半.
推论 同弧(或等弧)上的弦切角相等;同弧(或等弧)上的弦切角与圆周角相等.5.圆幂定理(1)相交弦定理:圆的两条相交弦,被交点分成的两条线段长的积相等.
推论 如果弦与直径垂直相交,那么弦的一半是它分直
径所成的两条线段的比例中项.
(2)割线定理:从圆外一点引圆的两条割线,这点到每条割线与圆的交点的两条线段长的积相等.(3)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆的交点的两条线段长的比例中项.
逆定理 从圆外一点引圆的割线,如果圆上一点与这点的连线是这点到割线与圆的交点的两条线段的比例中项,那么这点与圆上点的连线是圆的切线.题型一 分类讨论思想分类讨论是一种逻辑方法,也是一种数学思想.当我们面临的数学问题不能以统一形式解决时,可以把已知条件的范围划分为若干个子集,在各个子集内分别讨论问题的解,然后通过综合各类解而得到原问题的解答,这种解决问题的思想方法叫做分类讨论的思想方法.
应用分类讨论的思想方法解题的一般步骤是:
(1)确定讨论的对象以及被讨论对象的全域;
(2)合理分类,统一标准,不重不漏;
(3)逐段逐类讨论,分级进行;
(4)归纳总结,作出整个题目的结论.解 符合条件的圆有两种情况:规律方法 分析所给条件,正确把握C、D两点与直径AB的位置关系,从而确定分类的标准,以避免只考虑AC、AD在直径AB同侧或异侧一种情况.跟踪演练1 已知⊙O1与⊙O2相交于A,B,⊙O1的半径r1=5,⊙O2的半径r2=4,AB=6,求O1O2的长.解 ①若O1,O2在AB的异侧(如图(1)所示),O1O2垂直平分AB,题型二 化归思想
化归思想又称转化思想,是把待解决的问题或难解决的问题,通过某种转化过程,归结为一类已经解决或易解决的问题,最终求得问题的解答.在解决直线与圆的位置的有关问题时,常常需作辅助线,通过作辅助可将圆的问题化归为特殊三角形或四边形的问题,使问题得到解决.(1)证明 ∵∠ADE=∠B+∠BAD,
∠DAE=∠DAC+∠CAE,
又∠BAD=∠DAC,∠B=∠CAE,
∴∠ADE=∠DAE.∴AE=DE.
又DE是半圆的直径,
∴∠DFE=90°,∴AF=DF.规律方法 本题综合性较强,在(1)的证明中,把证明AF=DF的问题转化为证明AE=DE的问题,进而又转化为证明∠DAE=∠ADE的问题;在(2)的解答中,通过作辅助线,把求sin∠AED的问题转化为求sin∠AEG的问题,进而转化为求AG,AE的问题;在(3)的解答中,把求S△ABC的问题转化为求BC与AG的问题,如此等等,每一步都体现着转化与化归的思想方法.题型三 函数方程思想在直线与圆的位置关系中,涉及很多数量关系,既有角的大小,也有线段的长度,在求它们的大小时,有时不太方便,这时我们可以利用相似三角形或有关定理建立以欲求量为未知数的函数或方程,通过求函数的最值或解方程求出所要求的量,这种函数方程的思想在直线与圆的位置关系中有广泛的应用.例3 如图(1)所示,四边形ABCD是半径为1的半圆的内接等腰梯形,其下底是半圆的直径.写出该梯形的周长y与腰长x之间的函数关系式,当腰长为多少时,周长最长?并求出周长的最大值.解 如图(2)所示,过点O作OE⊥DC于点E,过点D作DF⊥AB于点F,连接OD.
设DE=m,OE=n,则DF=n,AF=AO-FO=1-m,且腰长x>0.规律方法 解本题的关键是建立周长y与腰长x之间的函数关系式.过点O作OE⊥DC,E为垂足,过点D作DF⊥AB,F为垂足,这样将四边形中的线段的长度计算问题转化为直角三角形中的边长的计算问题.题型四 数形结合思想数形结合思想是将抽象的数学语言与直观图形结合起来,使抽象思维与形象思维相结合,通过对图形的认识,数与形的转化,化抽象为具体,化难为易,使问题得到解决.规律方法 将计算与具体图形相结合是解决问题的关键,通过分析图形的位置关系,得到数量关系.跟踪演练4 两圆半径分别为4和2,如果它们有两条互相垂直的公切线,求它们的圆心距.体验高考答案 A解析 由切割线定理,知PA2=PC·PD,即62=3PD,解得PD=12,所以CD=PD-PC=9,又因为CE∶ED=2∶1,所以CE=6,ED=3.由相交弦定理,知AE·BE=CE·ED,即9BE=6×3,解得BE=2.
答案 2答案 8答案 5(1)证明 因为DE为⊙O直径,则∠BED+∠EDB=90°,
又BC⊥DE,
所以∠CBD+∠EDB=90°,从而∠CBD=∠BED.
又AB切⊙O于点B,得∠DBA=∠BED,
所以∠CBD=∠DBA.11.如图,⊙O和⊙O′相交于A,B两点,过A作两圆的切线分别交两圆于C,D两点,连结DB并延长交⊙O于点E.证明:
(1)AC·BD=AD·AB;
(2)AC=AE.
