第1讲 2 第1课时 极坐标系的概念
文档属性
| 名称 | 第1讲 2 第1课时 极坐标系的概念 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 12:41:43 | ||
图片预览







文档简介
课件27张PPT。第1课时 极坐标系的概念第一讲 二 极坐标系 学习目标
1.了解极坐标系的实际背景.
2.理解极坐标系的概念.
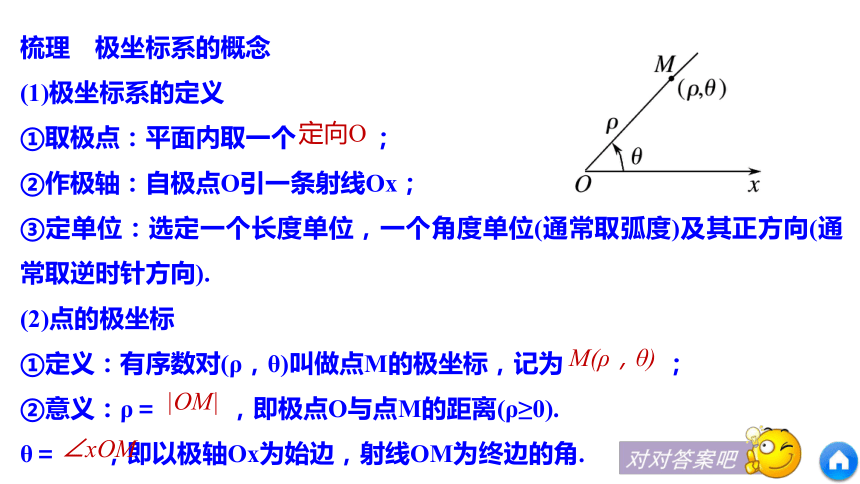
3.理解极坐标的多值性.问题导学达标检测题型探究内容索引问题导学知识点 极坐标系答案 能惟一确定;位置是由角和距离两个量确定的.思考1 某同学说他家在学校东偏北60°,且距学校1公里处,那么他说的位置能惟一确定吗?这个位置是由哪些量确定的?答案 选一个点O为基点,射线OA为参照方向.思考2 类比平面直角坐标系,怎样建立用角与距离确定平面上点的位置的坐标系?梳理 极坐标系的概念
(1)极坐标系的定义
①取极点:平面内取一个 ;
②作极轴:自极点O引一条射线Ox;
③定单位:选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向).
(2)点的极坐标
①定义:有序数对(ρ,θ)叫做点M的极坐标,记为 ;
②意义:ρ= ,即极点O与点M的距离(ρ≥0).
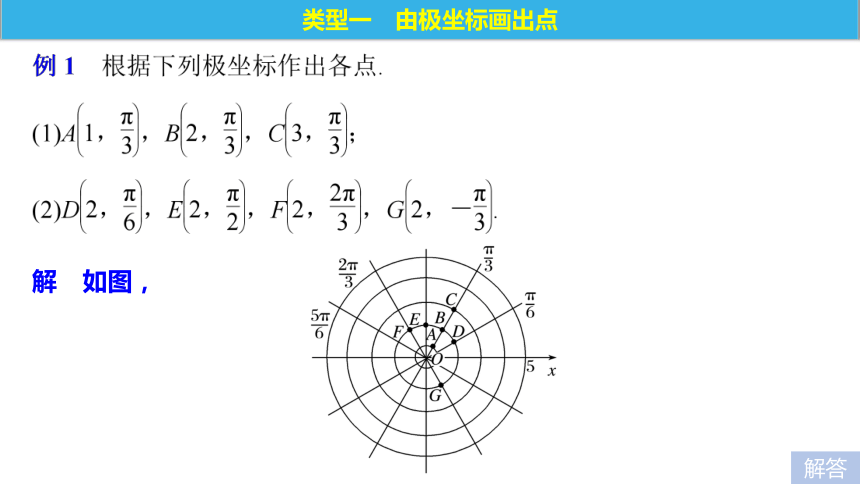
θ= ,即以极轴Ox为始边,射线OM为终边的角.定向OM(ρ,θ)|OM|∠xOM题型探究解 如图,类型一 由极坐标画出点解答反思与感悟 由极坐标作点,先由极角线找点所在角的终边,再由极径确定点的位置.通过作点可以看出“极角确定,极径变,点在一条线”,“极径不变,极角变,点在圆上转”.解 在极坐标系中,点A,B,C,D的位置是确定的.解答例2 设点A ,直线l为过极点且垂直于极轴的直线,分别求点A关于极轴,直线l,极点的对称点的极坐标(限定ρ>0,-π<θ≤π).类型二 求点的极坐标解答解 如图所示,引申探究
1.若将极角θ限定为0≤θ<2π,求例2中的点的极坐标.2.若将极角θ改为θ∈R,求例2中的点的极坐标.解答反思与感悟 (1)设点M的极坐标是(ρ,θ),则M点关于极点的对称点的极坐标是(-ρ,θ)或(ρ,θ+π);M点关于极轴的对称点的极坐标是(ρ,-θ);M点关于过极点且垂直于极轴的直线的对称点的极坐标是(ρ,π-θ)或(-ρ,-θ).
(2)点的极坐标不是惟一的,但若限制ρ>0,0≤θ<2π,则除极点外,点的极坐标是惟一确定的.
(3)写点的极坐标要注意顺序,极径ρ在前,极角θ在后,不能颠倒顺序.跟踪训练2 在极坐标系中,点A的极坐标是 ,求点A关于直线θ= 的对称点的极坐标(规定ρ>0,θ∈[0,2π)).解答例3 在极坐标系中,点O为极点,已知点A ,B ,求|AB|的值.类型三 极坐标系中两点间的距离解答∴△AOB为直角三角形,解答引申探究
在本例条件不变的情况下,求AB的中点的极坐标.解 取AB的中点M,连接OM,反思与感悟 在极坐标系中,如果P1(ρ1,θ1),P2(ρ2,θ2),那么两点间的距离公式|P1P2|= 的两种特殊情形为
①当θ1=θ2+2kπ,k∈Z时,|P1P2|=|ρ1-ρ2|;
②当θ1=θ2+π+2kπ,k∈Z时,|P1P2|=|ρ1+ρ2|.跟踪训练3 (1)在极坐标系中,已知两点P ,Q ,则线段PQ的长度为____.解析 作出图形,如图所示,可知OP与OQ垂直,所以线段PQ的长度|PQ|= =5.答案解析5(2)在极坐标系中,若△ABC的三个顶点为A ,B ,C ,判断三角形的形状.解 因为|AB|2=52+82-2×5×8×cos =49,
|AC|2=52+32-2×5×3×cos =49,
|BC|2=82+32-2×8×3×cos =49.
所以△ABC是等边三角形.解答达标检测答案1.极坐标系中,下列与点(1,π)相同的点为
A.(1,0) B.(2,π)
C.(1,2 016π) D.(1,2 017π)√12342.点M的直角坐标是(-1, ),则点M的极坐标为 答案√1234答案解析3.在极坐标系中,与点 关于极轴所在直线对称的点的极坐标是 √12344.在极坐标系中,已知A ,B 两点,则|AB|=_____.答案解析12341.极坐标系的四要素
①极点;②极轴;③长度单位;④角度单位和它的正方向.四者缺一不可.
2.在极坐标系中找点的位置,应先确定极角,再确定极径,最终确定点的位置.
3.确定点的极坐标的方法
点P的极坐标的一般形式为(ρ,θ+2kπ),k∈Z,则
(1)ρ为点P到极点的距离,是个定值.
(2)极角为满足θ+2kπ,k∈Z的任意角,不惟一,其中θ是始边在极轴上,终边过OP的任意一个角,一般取绝对值较小的角.规律与方法本课结束
1.了解极坐标系的实际背景.
2.理解极坐标系的概念.
3.理解极坐标的多值性.问题导学达标检测题型探究内容索引问题导学知识点 极坐标系答案 能惟一确定;位置是由角和距离两个量确定的.思考1 某同学说他家在学校东偏北60°,且距学校1公里处,那么他说的位置能惟一确定吗?这个位置是由哪些量确定的?答案 选一个点O为基点,射线OA为参照方向.思考2 类比平面直角坐标系,怎样建立用角与距离确定平面上点的位置的坐标系?梳理 极坐标系的概念
(1)极坐标系的定义
①取极点:平面内取一个 ;
②作极轴:自极点O引一条射线Ox;
③定单位:选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向).
(2)点的极坐标
①定义:有序数对(ρ,θ)叫做点M的极坐标,记为 ;
②意义:ρ= ,即极点O与点M的距离(ρ≥0).
θ= ,即以极轴Ox为始边,射线OM为终边的角.定向OM(ρ,θ)|OM|∠xOM题型探究解 如图,类型一 由极坐标画出点解答反思与感悟 由极坐标作点,先由极角线找点所在角的终边,再由极径确定点的位置.通过作点可以看出“极角确定,极径变,点在一条线”,“极径不变,极角变,点在圆上转”.解 在极坐标系中,点A,B,C,D的位置是确定的.解答例2 设点A ,直线l为过极点且垂直于极轴的直线,分别求点A关于极轴,直线l,极点的对称点的极坐标(限定ρ>0,-π<θ≤π).类型二 求点的极坐标解答解 如图所示,引申探究
1.若将极角θ限定为0≤θ<2π,求例2中的点的极坐标.2.若将极角θ改为θ∈R,求例2中的点的极坐标.解答反思与感悟 (1)设点M的极坐标是(ρ,θ),则M点关于极点的对称点的极坐标是(-ρ,θ)或(ρ,θ+π);M点关于极轴的对称点的极坐标是(ρ,-θ);M点关于过极点且垂直于极轴的直线的对称点的极坐标是(ρ,π-θ)或(-ρ,-θ).
(2)点的极坐标不是惟一的,但若限制ρ>0,0≤θ<2π,则除极点外,点的极坐标是惟一确定的.
(3)写点的极坐标要注意顺序,极径ρ在前,极角θ在后,不能颠倒顺序.跟踪训练2 在极坐标系中,点A的极坐标是 ,求点A关于直线θ= 的对称点的极坐标(规定ρ>0,θ∈[0,2π)).解答例3 在极坐标系中,点O为极点,已知点A ,B ,求|AB|的值.类型三 极坐标系中两点间的距离解答∴△AOB为直角三角形,解答引申探究
在本例条件不变的情况下,求AB的中点的极坐标.解 取AB的中点M,连接OM,反思与感悟 在极坐标系中,如果P1(ρ1,θ1),P2(ρ2,θ2),那么两点间的距离公式|P1P2|= 的两种特殊情形为
①当θ1=θ2+2kπ,k∈Z时,|P1P2|=|ρ1-ρ2|;
②当θ1=θ2+π+2kπ,k∈Z时,|P1P2|=|ρ1+ρ2|.跟踪训练3 (1)在极坐标系中,已知两点P ,Q ,则线段PQ的长度为____.解析 作出图形,如图所示,可知OP与OQ垂直,所以线段PQ的长度|PQ|= =5.答案解析5(2)在极坐标系中,若△ABC的三个顶点为A ,B ,C ,判断三角形的形状.解 因为|AB|2=52+82-2×5×8×cos =49,
|AC|2=52+32-2×5×3×cos =49,
|BC|2=82+32-2×8×3×cos =49.
所以△ABC是等边三角形.解答达标检测答案1.极坐标系中,下列与点(1,π)相同的点为
A.(1,0) B.(2,π)
C.(1,2 016π) D.(1,2 017π)√12342.点M的直角坐标是(-1, ),则点M的极坐标为 答案√1234答案解析3.在极坐标系中,与点 关于极轴所在直线对称的点的极坐标是 √12344.在极坐标系中,已知A ,B 两点,则|AB|=_____.答案解析12341.极坐标系的四要素
①极点;②极轴;③长度单位;④角度单位和它的正方向.四者缺一不可.
2.在极坐标系中找点的位置,应先确定极角,再确定极径,最终确定点的位置.
3.确定点的极坐标的方法
点P的极坐标的一般形式为(ρ,θ+2kπ),k∈Z,则
(1)ρ为点P到极点的距离,是个定值.
(2)极角为满足θ+2kπ,k∈Z的任意角,不惟一,其中θ是始边在极轴上,终边过OP的任意一个角,一般取绝对值较小的角.规律与方法本课结束
