第1讲 3 第1课时 圆的极坐标方程
文档属性
| 名称 | 第1讲 3 第1课时 圆的极坐标方程 |

|
|
| 格式 | zip | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 12:42:42 | ||
图片预览









文档简介
课件37张PPT。第1课时 圆的极坐标方程第一讲 三 简单曲线的极坐标方程学习目标
1.了解极坐标方程的意义.
2.掌握圆的极坐标方程.
3.能根据极坐标方程研究曲线的有关性质.问题导学达标检测题型探究内容索引问题导学(1)在极坐标系中,如果曲线C上 的极坐标中 有一个满足方程f(ρ,θ)=0,并且坐标适合方程f(ρ,θ)=0的点 ,那么方程f(ρ,θ)=0叫做曲线C的 .
(2)建立曲线的极坐标方程的方法步骤
①建立适当的极坐标系,设P(ρ,θ)是曲线上任意一点;
②列出曲线上任意一点的极径与极角之间的关系式;
③将列出的关系式整理、化简;
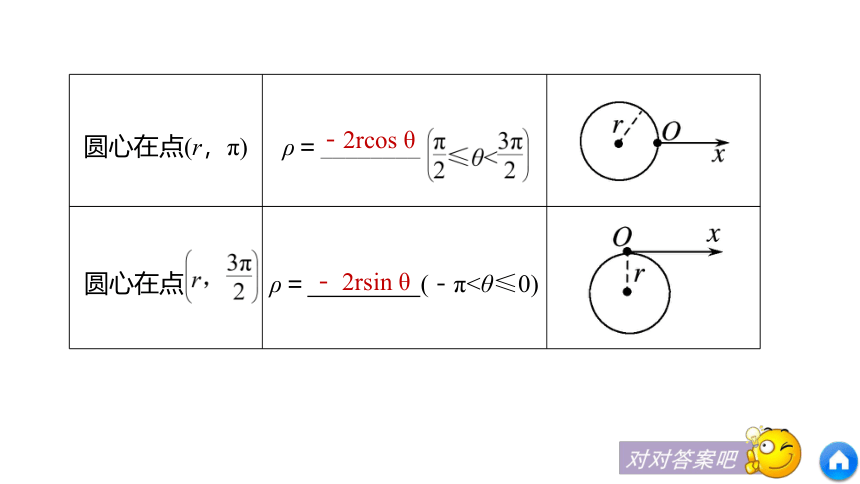
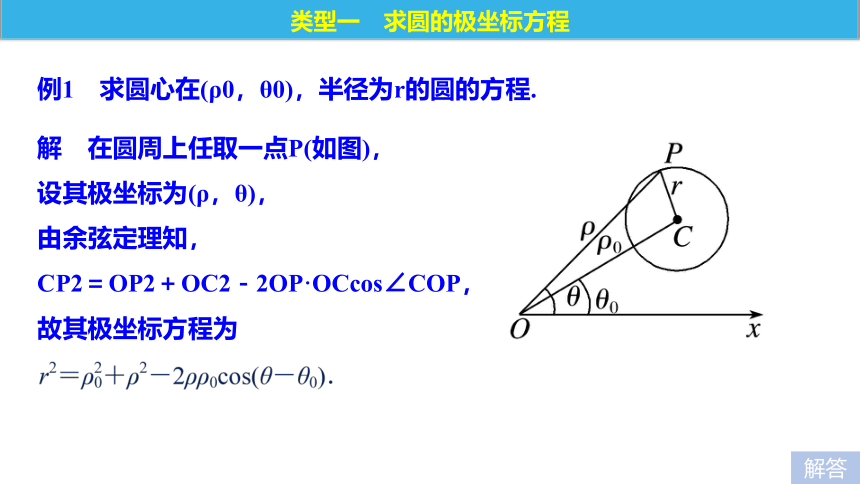
④证明所得方程就是曲线的极坐标方程.知识点一 曲线的极坐标方程任意一点至少都在曲线C上极坐标方程知识点二 圆的极坐标方程答案 不一定.思考1 在极坐标系中,点M(ρ,θ)的轨迹方程中一定含有ρ或θ吗?答案 ρ=2.思考2 圆心在极点,半径为2的圆的极坐标方程是什么?梳理 圆的极坐标方程r2rcos θ2rsin θ-2rcos θ- 2rsin θ题型探究例1 求圆心在(ρ0,θ0),半径为r的圆的方程.类型一 求圆的极坐标方程解答解 在圆周上任取一点P(如图),
设其极坐标为(ρ,θ),
由余弦定理知,
CP2=OP2+OC2-2OP·OCcos∠COP,
故其极坐标方程为引申探究
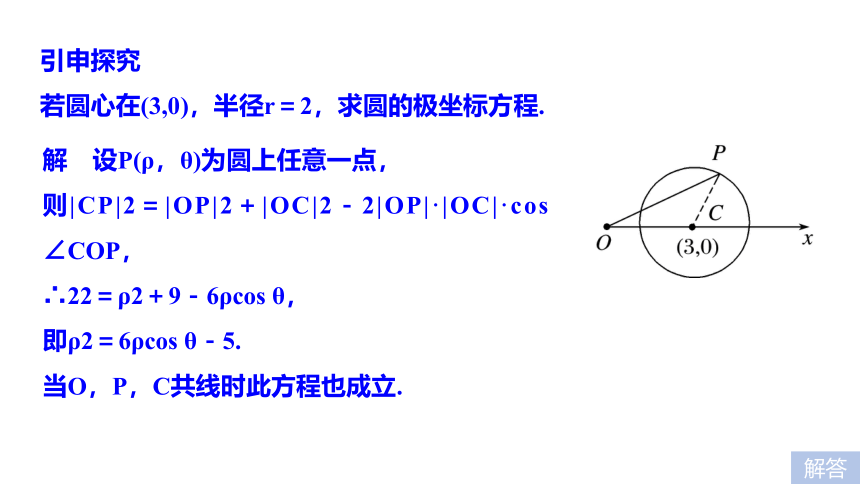
若圆心在(3,0),半径r=2,求圆的极坐标方程.解 设P(ρ,θ)为圆上任意一点,
则|CP|2=|OP|2+|OC|2-2|OP|·|OC|·cos ∠COP,
∴22=ρ2+9-6ρcos θ,
即ρ2=6ρcos θ-5.
当O,P,C共线时此方程也成立.解答反思与感悟 求圆的极坐标方程的步骤
(1)设圆上任意一点的极坐标为M(ρ,θ).
(2)在极点、圆心与M构成的三角形中运用余弦定理或解直角三角形列出方程f(ρ,θ)=0并化简.
(3)验证极点、圆心与M三点共线时,点M(ρ,θ)的极坐标也适合上述极坐标方程.跟踪训练1 在极坐标系中,已知圆C的圆心为C ,半径为r=3.求圆C的极坐标方程.解 设M(ρ,θ)为圆C上任一点,
易知极点O在圆C上,设OM的中点为N,
∴△OCM为等腰三角形,解答命题角度1 直角坐标方程化极坐标方程
例2 把下列直角坐标方程化为极坐标方程.
(1)x2+y2=1;类型二 极坐标方程与直角坐标方程的互化解答∵(ρcos θ)2+(ρsin θ)2=1,
∴ρ2=1,即ρ=1.解 ∵(ρcos θ)2+(ρsin θ)2-4ρcos θ+4=0,
∴ρ2-4ρcos θ+4=0.(2)x2+y2-4x+4=0;(3)x2+y2-2x-2y-2=0.解答解 ∵(ρcos θ)2+(ρsin θ)2-2ρcos θ-2ρsin θ-2=0.
∴ρ2-2ρ(cos θ+sin θ)-2=0,反思与感悟 在进行两种坐标方程间的互化时,要注意
(1)互化公式是有三个前提条件的,即极点与直角坐标系的原点重合、极轴与直角坐标系的横轴的正半轴重合,两种坐标系的单位长度相同.
(2)由直角坐标求极坐标时,理论上不是惟一的,但这里约定只在0≤θ<2π范围内求值.解 将x=ρcos θ,y=ρsin θ代入x2+y2-2x-1=0,
得(ρcos θ)2+(ρsin θ)2-2ρcos θ-1=0,
化简,得ρ2-2ρcos θ-1=0.跟踪训练2 把下列直角坐标方程化为极坐标方程.
(1)y2=4x;解答解 将x=ρcos θ,y=ρsin θ代入y2=4x,
得(ρsin θ)2=4ρcos θ,化简,得ρsin2θ=4cos θ.(2)x2+y2-2x-1=0.命题角度2 极坐标方程化直角坐标方程
例3 把下列极坐标方程化为直角坐标方程.解答(1)ρ2cos 2θ=1; 解 ∵ρ2cos 2θ=1,∴ρ2cos2θ-ρ2sin2θ=1,
∴化为直角坐标方程为x2-y2=1.∴ρcos θ-ρsin θ-1=0.
又ρcos θ=x,ρsin θ=y,∴x-y-1=0.解答解答反思与感悟 由极坐标方程化为直角坐标方程时要注意变形的等价性,通常总要用ρ去乘方程的两端,应该检查极点是否在曲线上,若在,是等价变形,否则,不是等价变形.跟踪训练3 把下列直角坐标方程与极坐标方程进行互化.
(1)x2+y2-2x=0;解答解 ∵x2+y2-2x=0,
∴ρ2-2ρcos θ=0.∴ρ=2cos θ.解 ∵ρ=cos θ-2sin θ,∴ρ2=ρcos θ-2ρsin θ.
∴x2+y2=x-2y,即x2+y2-x+2y=0.(2)ρ=cos θ-2sin θ;解 ∵ρ2=cos2θ,∴ρ4=ρ2cos2θ=(ρcos θ)2.
∴(x2+y2)2=x2,
即x2+y2=x或x2+y2=-x.(3)ρ2=cos2θ.解答例4 若曲线C的极坐标方程为ρ=2sin θ+4cos θ,以极点为原点,极轴为x轴的正半轴建立直角坐标系.
(1)求曲线C的直角坐标方程;类型三 直角坐标与极坐标方程互化的应用解答由ρ=2sin θ+4cos θ,得ρ2=2ρsin θ+4ρcos θ,
∴x2+y2-4x-2y=0,即(x-2)2+(y-1)2=5.(2)若曲线ρsin =0与曲线C相交于A,B,求|AB|的值.即ρsin θ-ρcos θ=0,∴x-y=0.解答反思与感悟 在研究曲线的性质时,如交点、距离等,如果用极坐标不方便,可以转化为直角坐标方程,反之,可以转化为极坐标方程.跟踪训练4 在极坐标系中,曲线C1和C2的方程分别为ρsin2θ=cos θ和ρsin θ=1,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,则曲线C1和C2交点的直角坐标为______.答案(1,1)达标检测答案1.极坐标方程分别为ρ=cos θ和ρ=sin θ的两个圆的圆心距是
A.3 B. C.1 D.12345√2.将极坐标方程ρ2cos θ-ρ=0化为直角坐标方程为
A.x2+y2=0或y=1 B.x=1
C.x2+y2=0或x=1 D.y=112345√答案答案解析3.在极坐标系中,圆ρ=2sin θ的圆心的极坐标是 12345√解析 由ρ=2sin θ,得ρ2=2ρsin θ,
化为直角坐标方程为x2+y2-2y=0,
即x2+(y-1)2=1,
圆心坐标为(0,1),∴它表示的曲线为抛物线.4.4ρsin2 =5表示的曲线是
A.圆 B.椭圆
C.双曲线的一支 D.抛物线 12345答案解析√123455.在极坐标系中,已知圆C的圆心为C ,半径为1,求圆C的极坐标方程.解答12345解 在圆C上任取一点P(ρ,θ),在△POC中,
由余弦定理可得
CP2=OC2+OP2-2OC·OP·cos∠POC,当O,P,C共线时,此方程也成立,1.曲线的极坐标方程与直角坐标方程的区别
由于平面上点的极坐标的表示形式不惟一,即(ρ,θ),(ρ,2π+θ),(-ρ,π+θ),(-ρ,-π+θ)都表示同一点的坐标,这与点的直角坐标的惟一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程规律与方法本课结束
1.了解极坐标方程的意义.
2.掌握圆的极坐标方程.
3.能根据极坐标方程研究曲线的有关性质.问题导学达标检测题型探究内容索引问题导学(1)在极坐标系中,如果曲线C上 的极坐标中 有一个满足方程f(ρ,θ)=0,并且坐标适合方程f(ρ,θ)=0的点 ,那么方程f(ρ,θ)=0叫做曲线C的 .
(2)建立曲线的极坐标方程的方法步骤
①建立适当的极坐标系,设P(ρ,θ)是曲线上任意一点;
②列出曲线上任意一点的极径与极角之间的关系式;
③将列出的关系式整理、化简;
④证明所得方程就是曲线的极坐标方程.知识点一 曲线的极坐标方程任意一点至少都在曲线C上极坐标方程知识点二 圆的极坐标方程答案 不一定.思考1 在极坐标系中,点M(ρ,θ)的轨迹方程中一定含有ρ或θ吗?答案 ρ=2.思考2 圆心在极点,半径为2的圆的极坐标方程是什么?梳理 圆的极坐标方程r2rcos θ2rsin θ-2rcos θ- 2rsin θ题型探究例1 求圆心在(ρ0,θ0),半径为r的圆的方程.类型一 求圆的极坐标方程解答解 在圆周上任取一点P(如图),
设其极坐标为(ρ,θ),
由余弦定理知,
CP2=OP2+OC2-2OP·OCcos∠COP,
故其极坐标方程为引申探究
若圆心在(3,0),半径r=2,求圆的极坐标方程.解 设P(ρ,θ)为圆上任意一点,
则|CP|2=|OP|2+|OC|2-2|OP|·|OC|·cos ∠COP,
∴22=ρ2+9-6ρcos θ,
即ρ2=6ρcos θ-5.
当O,P,C共线时此方程也成立.解答反思与感悟 求圆的极坐标方程的步骤
(1)设圆上任意一点的极坐标为M(ρ,θ).
(2)在极点、圆心与M构成的三角形中运用余弦定理或解直角三角形列出方程f(ρ,θ)=0并化简.
(3)验证极点、圆心与M三点共线时,点M(ρ,θ)的极坐标也适合上述极坐标方程.跟踪训练1 在极坐标系中,已知圆C的圆心为C ,半径为r=3.求圆C的极坐标方程.解 设M(ρ,θ)为圆C上任一点,
易知极点O在圆C上,设OM的中点为N,
∴△OCM为等腰三角形,解答命题角度1 直角坐标方程化极坐标方程
例2 把下列直角坐标方程化为极坐标方程.
(1)x2+y2=1;类型二 极坐标方程与直角坐标方程的互化解答∵(ρcos θ)2+(ρsin θ)2=1,
∴ρ2=1,即ρ=1.解 ∵(ρcos θ)2+(ρsin θ)2-4ρcos θ+4=0,
∴ρ2-4ρcos θ+4=0.(2)x2+y2-4x+4=0;(3)x2+y2-2x-2y-2=0.解答解 ∵(ρcos θ)2+(ρsin θ)2-2ρcos θ-2ρsin θ-2=0.
∴ρ2-2ρ(cos θ+sin θ)-2=0,反思与感悟 在进行两种坐标方程间的互化时,要注意
(1)互化公式是有三个前提条件的,即极点与直角坐标系的原点重合、极轴与直角坐标系的横轴的正半轴重合,两种坐标系的单位长度相同.
(2)由直角坐标求极坐标时,理论上不是惟一的,但这里约定只在0≤θ<2π范围内求值.解 将x=ρcos θ,y=ρsin θ代入x2+y2-2x-1=0,
得(ρcos θ)2+(ρsin θ)2-2ρcos θ-1=0,
化简,得ρ2-2ρcos θ-1=0.跟踪训练2 把下列直角坐标方程化为极坐标方程.
(1)y2=4x;解答解 将x=ρcos θ,y=ρsin θ代入y2=4x,
得(ρsin θ)2=4ρcos θ,化简,得ρsin2θ=4cos θ.(2)x2+y2-2x-1=0.命题角度2 极坐标方程化直角坐标方程
例3 把下列极坐标方程化为直角坐标方程.解答(1)ρ2cos 2θ=1; 解 ∵ρ2cos 2θ=1,∴ρ2cos2θ-ρ2sin2θ=1,
∴化为直角坐标方程为x2-y2=1.∴ρcos θ-ρsin θ-1=0.
又ρcos θ=x,ρsin θ=y,∴x-y-1=0.解答解答反思与感悟 由极坐标方程化为直角坐标方程时要注意变形的等价性,通常总要用ρ去乘方程的两端,应该检查极点是否在曲线上,若在,是等价变形,否则,不是等价变形.跟踪训练3 把下列直角坐标方程与极坐标方程进行互化.
(1)x2+y2-2x=0;解答解 ∵x2+y2-2x=0,
∴ρ2-2ρcos θ=0.∴ρ=2cos θ.解 ∵ρ=cos θ-2sin θ,∴ρ2=ρcos θ-2ρsin θ.
∴x2+y2=x-2y,即x2+y2-x+2y=0.(2)ρ=cos θ-2sin θ;解 ∵ρ2=cos2θ,∴ρ4=ρ2cos2θ=(ρcos θ)2.
∴(x2+y2)2=x2,
即x2+y2=x或x2+y2=-x.(3)ρ2=cos2θ.解答例4 若曲线C的极坐标方程为ρ=2sin θ+4cos θ,以极点为原点,极轴为x轴的正半轴建立直角坐标系.
(1)求曲线C的直角坐标方程;类型三 直角坐标与极坐标方程互化的应用解答由ρ=2sin θ+4cos θ,得ρ2=2ρsin θ+4ρcos θ,
∴x2+y2-4x-2y=0,即(x-2)2+(y-1)2=5.(2)若曲线ρsin =0与曲线C相交于A,B,求|AB|的值.即ρsin θ-ρcos θ=0,∴x-y=0.解答反思与感悟 在研究曲线的性质时,如交点、距离等,如果用极坐标不方便,可以转化为直角坐标方程,反之,可以转化为极坐标方程.跟踪训练4 在极坐标系中,曲线C1和C2的方程分别为ρsin2θ=cos θ和ρsin θ=1,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,则曲线C1和C2交点的直角坐标为______.答案(1,1)达标检测答案1.极坐标方程分别为ρ=cos θ和ρ=sin θ的两个圆的圆心距是
A.3 B. C.1 D.12345√2.将极坐标方程ρ2cos θ-ρ=0化为直角坐标方程为
A.x2+y2=0或y=1 B.x=1
C.x2+y2=0或x=1 D.y=112345√答案答案解析3.在极坐标系中,圆ρ=2sin θ的圆心的极坐标是 12345√解析 由ρ=2sin θ,得ρ2=2ρsin θ,
化为直角坐标方程为x2+y2-2y=0,
即x2+(y-1)2=1,
圆心坐标为(0,1),∴它表示的曲线为抛物线.4.4ρsin2 =5表示的曲线是
A.圆 B.椭圆
C.双曲线的一支 D.抛物线 12345答案解析√123455.在极坐标系中,已知圆C的圆心为C ,半径为1,求圆C的极坐标方程.解答12345解 在圆C上任取一点P(ρ,θ),在△POC中,
由余弦定理可得
CP2=OC2+OP2-2OC·OP·cos∠POC,当O,P,C共线时,此方程也成立,1.曲线的极坐标方程与直角坐标方程的区别
由于平面上点的极坐标的表示形式不惟一,即(ρ,θ),(ρ,2π+θ),(-ρ,π+θ),(-ρ,-π+θ)都表示同一点的坐标,这与点的直角坐标的惟一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程规律与方法本课结束
