第2讲 参数方程复习课
图片预览










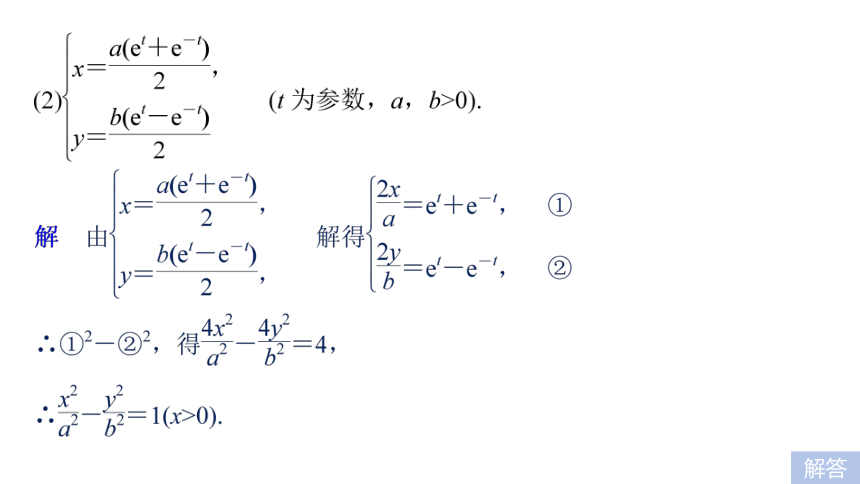

文档简介
课件42张PPT。第二讲 参数方程复习课学习目标
1.梳理知识要点,构建知识网络.
2.进一步巩固对参数方程等相关概念的理解和认识.
3.能综合应用极坐标、参数方程解决问题.知识梳理达标检测题型探究内容索引知识梳理1.参数方程的定义
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数 ①并且对于t的每一个允许值,由方程组①所确定的点M(x,y)都在这条曲线上,那么方程组①就叫做这条曲线的 ,联系变数x,y的变数t叫做参变数,简称参数.参数方程中的参数可以是有物理意义或几何意义的变数,也可以是没有明显实际意义的变数.参数方程2.常见曲线的参数方程
(1)直线
过定点M0(x0,y0),倾斜角为α的直线l的参数方程的标准形式为
__________________________.
(2)圆
①圆x2+y2=r2的参数方程为______________________;
②圆(x-a)2+(y-b)2=r2的参数方程为________________________.(3)椭圆
中心在原点,对称轴为坐标轴的椭圆b2x2+a2y2=a2b2(a>b>0)的参数方程为______________________.
(4)双曲线
中心在原点,对称轴为坐标轴的双曲线b2x2-a2y2=a2b2(a>0,b>0)的参数方程为______________________.(5)抛物线
抛物线y2=2px(p>0)的参数方程为_______________________
或____________________.题型探究即5x2+4xy+17y2-81=0.类型一 参数方程化为普通方程例1 把下列参数方程化为普通方程:解答解 关于cos θ,sin θ的方程组解答反思与感悟 参数方程化为普通方程的注意事项
(1)在参数方程与普通方程的互化中,必须使x,y的取值范围保持一致,由参数方程化为普通方程时需要考虑x的取值范围,注意参数方程与消去参数后所得的普通方程同解性的判定.
(2)消除参数的常用方法:①代入消参法;②三角消参法;③根据参数方程的特征,采用特殊的消参手段.跟踪训练1 判断方程 (θ是参数且θ∈(0,π))表示的曲线的形状.解答类型二 参数方程的应用命题角度1 直线参数方程的应用
例2 已知点P(3,2)平分抛物线y2=4x的一条弦AB,求弦AB的长.解答代入方程y2=4x整理,得t2sin2α+4(sin α-cos α)t-8=0. ①
∵点P(3,2)是弦AB的中点,
由参数t的几何意义可知,方程①的两个实根t1,t2满足关系t1+t2=0.反思与感悟 应用直线的参数方程求弦长要注意的问题
(1)直线的参数方程应为标准形式.
(2)要注意直线倾斜角的取值范围.
(3)设直线上两点对应的参数分别为t1,t2.
(4)套公式|t1-t2|求弦长.跟踪训练2 直线l过点P0(-4,0),它的参数方程为 (t为参数),直线l与圆x2+y2=7相交于A,B两点.
(1)求弦长|AB|;解答解 将直线l的参数方程代入圆的方程,设A和B两点对应的参数分别为t1和t2,由根与系数的关系,(2)过P0作圆的切线,求切线长.解答解 设圆过P0的切线为P0T,T在圆上,
则|P0T|2=|P0A|·|P0B|=|t1t2|=9,
∴切线长|P0T|=3.命题角度2 曲线参数方程的应用
例3 在平面直角坐标系xOy中,曲线C的参数方程为 (α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin =2 .
(1)求曲线C与直线l在该直角坐标系下的普通方程;解答可得(x-2)2+y2=1,可得ρ(sin θ+cos θ)=4,
即x+y=4.(2)动点A在曲线C上,动点B在直线l上,定点P(-1,1),求|PB|+|AB|的最小值.解答解 方法一 设P关于直线l的对称点为Q(a,b),所以Q(3,5),
由(1)知曲线C为圆,圆心C(2,0),半径r=1,
|PB|+|AB|=|QB|+|AB|≥|QC|-1.
仅当Q,B,A,C四点共线时,且A在B,C之间时等号成立,反思与感悟 (1)关于折线段的长度和或长度差的最大值或最小值的求法,常常利用对称性以及两点之间线段最短解决.
(2)有关点与圆、直线与圆的最大值或最小值问题,常常转化为经过圆心的直线、圆心到直线的距离等.直线l的普通方程为2x+y-6=0.解答(1)写出曲线C的参数方程,直线l的普通方程;解答(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.类型三 极坐标与参数方程解答例4 在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.
(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;解 由x=ρcos θ,y=ρsin θ,
可得圆C的极坐标方程为ρ2+12ρcos θ+11=0.解答解 方法一 在(1)中建立的极坐标系中,直线l的极坐标方程为θ=α(ρ∈R).
设A,B所对应的极径分别为ρ1,ρ2,将l的极坐标方程代入C的极坐标方程,得ρ2+12ρcos α+11=0.
于是ρ1+ρ2=-12cos α,ρ1ρ2=11.得t2+(12cos α)t+11=0,
设A,B对应的参数为t1,t2,
所以t1+t2=-12cos α,t1t2=11.反思与感悟 (1)极坐标与参数方程综合是高考的重点、热点.
(2)解决此类问题一般可以转化为直角坐标下求解.当然也可以转化为极坐标下求解,关键是根据题目特点合理转化.跟踪训练4 在平面直角坐标系xOy中,曲线C的参数方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为3ρcos θ+2ρsin θ=12.
(1)求曲线C的普通方程和直线l的直角坐标方程;解答在3ρcos θ+2ρsin θ=12中,由ρcos θ=x,ρsin θ=y,
得3x+2y-12=0,
所以直线l的直角坐标方程为3x+2y-12=0.解答(2)若直线l与曲线C交于A,B两点,M为曲线C与y轴负半轴的交点,求四边形OMAB的面积.易得A(4,0),B(2,3),达标检测1.曲线 (θ为参数)的焦点坐标为
A.(±3,0) B.(0,±3)
C.(±6,0) D.(0,±6)解析答案12345√这是焦点在y轴上的椭圆,c2=a2-b2=62,
所以焦点坐标为(0,±6).√答案123453.已知直线l的参数方程为 (t为参数),圆C的极坐标方程为
ρ=2 sin θ,则直线l与圆C的位置关系为
A.相离 B.相切
C.相交 D.由参数确定答案√123454.点P(1,0)到曲线 (t为参数)上的点的最短距离为___.解析 设点P(1,0)到曲线上的点的距离为d,所以点P到曲线上的点的距离的最小值为1.解析答案1123455.在平面直角坐标系xOy中,设P(x,y)是椭圆 +y2=1上的一个动点,求S=x+y的最大值和最小值.解答12345规律与方法1.参数方程是以参变量为中介来表示曲线上点的坐标的方程,是曲线在同一坐标系下的又一种表示形式.某些曲线上点的坐标,用普通方程描述它们之间的关系比较困难,甚至不可能,列出的方程既复杂又不易理解,而用参数方程来描述曲线上点的坐标的间接关系比较方便,学习参数方程有助于进一步体会数学方法的灵活多变,提高应用意识和实践能力.
2.参数方程、极坐标方程是解析几何曲线方程的另外两种巧妙的表达形式,解题时要善于根据解题的需求将参数方程与普通方程进行互化,达到方便解题的目的,同时注意参数的范围.本课结束
1.梳理知识要点,构建知识网络.
2.进一步巩固对参数方程等相关概念的理解和认识.
3.能综合应用极坐标、参数方程解决问题.知识梳理达标检测题型探究内容索引知识梳理1.参数方程的定义
一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数 ①并且对于t的每一个允许值,由方程组①所确定的点M(x,y)都在这条曲线上,那么方程组①就叫做这条曲线的 ,联系变数x,y的变数t叫做参变数,简称参数.参数方程中的参数可以是有物理意义或几何意义的变数,也可以是没有明显实际意义的变数.参数方程2.常见曲线的参数方程
(1)直线
过定点M0(x0,y0),倾斜角为α的直线l的参数方程的标准形式为
__________________________.
(2)圆
①圆x2+y2=r2的参数方程为______________________;
②圆(x-a)2+(y-b)2=r2的参数方程为________________________.(3)椭圆
中心在原点,对称轴为坐标轴的椭圆b2x2+a2y2=a2b2(a>b>0)的参数方程为______________________.
(4)双曲线
中心在原点,对称轴为坐标轴的双曲线b2x2-a2y2=a2b2(a>0,b>0)的参数方程为______________________.(5)抛物线
抛物线y2=2px(p>0)的参数方程为_______________________
或____________________.题型探究即5x2+4xy+17y2-81=0.类型一 参数方程化为普通方程例1 把下列参数方程化为普通方程:解答解 关于cos θ,sin θ的方程组解答反思与感悟 参数方程化为普通方程的注意事项
(1)在参数方程与普通方程的互化中,必须使x,y的取值范围保持一致,由参数方程化为普通方程时需要考虑x的取值范围,注意参数方程与消去参数后所得的普通方程同解性的判定.
(2)消除参数的常用方法:①代入消参法;②三角消参法;③根据参数方程的特征,采用特殊的消参手段.跟踪训练1 判断方程 (θ是参数且θ∈(0,π))表示的曲线的形状.解答类型二 参数方程的应用命题角度1 直线参数方程的应用
例2 已知点P(3,2)平分抛物线y2=4x的一条弦AB,求弦AB的长.解答代入方程y2=4x整理,得t2sin2α+4(sin α-cos α)t-8=0. ①
∵点P(3,2)是弦AB的中点,
由参数t的几何意义可知,方程①的两个实根t1,t2满足关系t1+t2=0.反思与感悟 应用直线的参数方程求弦长要注意的问题
(1)直线的参数方程应为标准形式.
(2)要注意直线倾斜角的取值范围.
(3)设直线上两点对应的参数分别为t1,t2.
(4)套公式|t1-t2|求弦长.跟踪训练2 直线l过点P0(-4,0),它的参数方程为 (t为参数),直线l与圆x2+y2=7相交于A,B两点.
(1)求弦长|AB|;解答解 将直线l的参数方程代入圆的方程,设A和B两点对应的参数分别为t1和t2,由根与系数的关系,(2)过P0作圆的切线,求切线长.解答解 设圆过P0的切线为P0T,T在圆上,
则|P0T|2=|P0A|·|P0B|=|t1t2|=9,
∴切线长|P0T|=3.命题角度2 曲线参数方程的应用
例3 在平面直角坐标系xOy中,曲线C的参数方程为 (α为参数),在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,直线l的极坐标方程为ρsin =2 .
(1)求曲线C与直线l在该直角坐标系下的普通方程;解答可得(x-2)2+y2=1,可得ρ(sin θ+cos θ)=4,
即x+y=4.(2)动点A在曲线C上,动点B在直线l上,定点P(-1,1),求|PB|+|AB|的最小值.解答解 方法一 设P关于直线l的对称点为Q(a,b),所以Q(3,5),
由(1)知曲线C为圆,圆心C(2,0),半径r=1,
|PB|+|AB|=|QB|+|AB|≥|QC|-1.
仅当Q,B,A,C四点共线时,且A在B,C之间时等号成立,反思与感悟 (1)关于折线段的长度和或长度差的最大值或最小值的求法,常常利用对称性以及两点之间线段最短解决.
(2)有关点与圆、直线与圆的最大值或最小值问题,常常转化为经过圆心的直线、圆心到直线的距离等.直线l的普通方程为2x+y-6=0.解答(1)写出曲线C的参数方程,直线l的普通方程;解答(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.类型三 极坐标与参数方程解答例4 在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.
(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;解 由x=ρcos θ,y=ρsin θ,
可得圆C的极坐标方程为ρ2+12ρcos θ+11=0.解答解 方法一 在(1)中建立的极坐标系中,直线l的极坐标方程为θ=α(ρ∈R).
设A,B所对应的极径分别为ρ1,ρ2,将l的极坐标方程代入C的极坐标方程,得ρ2+12ρcos α+11=0.
于是ρ1+ρ2=-12cos α,ρ1ρ2=11.得t2+(12cos α)t+11=0,
设A,B对应的参数为t1,t2,
所以t1+t2=-12cos α,t1t2=11.反思与感悟 (1)极坐标与参数方程综合是高考的重点、热点.
(2)解决此类问题一般可以转化为直角坐标下求解.当然也可以转化为极坐标下求解,关键是根据题目特点合理转化.跟踪训练4 在平面直角坐标系xOy中,曲线C的参数方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为3ρcos θ+2ρsin θ=12.
(1)求曲线C的普通方程和直线l的直角坐标方程;解答在3ρcos θ+2ρsin θ=12中,由ρcos θ=x,ρsin θ=y,
得3x+2y-12=0,
所以直线l的直角坐标方程为3x+2y-12=0.解答(2)若直线l与曲线C交于A,B两点,M为曲线C与y轴负半轴的交点,求四边形OMAB的面积.易得A(4,0),B(2,3),达标检测1.曲线 (θ为参数)的焦点坐标为
A.(±3,0) B.(0,±3)
C.(±6,0) D.(0,±6)解析答案12345√这是焦点在y轴上的椭圆,c2=a2-b2=62,
所以焦点坐标为(0,±6).√答案123453.已知直线l的参数方程为 (t为参数),圆C的极坐标方程为
ρ=2 sin θ,则直线l与圆C的位置关系为
A.相离 B.相切
C.相交 D.由参数确定答案√123454.点P(1,0)到曲线 (t为参数)上的点的最短距离为___.解析 设点P(1,0)到曲线上的点的距离为d,所以点P到曲线上的点的距离的最小值为1.解析答案1123455.在平面直角坐标系xOy中,设P(x,y)是椭圆 +y2=1上的一个动点,求S=x+y的最大值和最小值.解答12345规律与方法1.参数方程是以参变量为中介来表示曲线上点的坐标的方程,是曲线在同一坐标系下的又一种表示形式.某些曲线上点的坐标,用普通方程描述它们之间的关系比较困难,甚至不可能,列出的方程既复杂又不易理解,而用参数方程来描述曲线上点的坐标的间接关系比较方便,学习参数方程有助于进一步体会数学方法的灵活多变,提高应用意识和实践能力.
2.参数方程、极坐标方程是解析几何曲线方程的另外两种巧妙的表达形式,解题时要善于根据解题的需求将参数方程与普通方程进行互化,达到方便解题的目的,同时注意参数的范围.本课结束
