第2讲 不等式的基本方法-综合法与分析法
文档属性
| 名称 | 第2讲 不等式的基本方法-综合法与分析法 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 00:00:00 | ||
图片预览










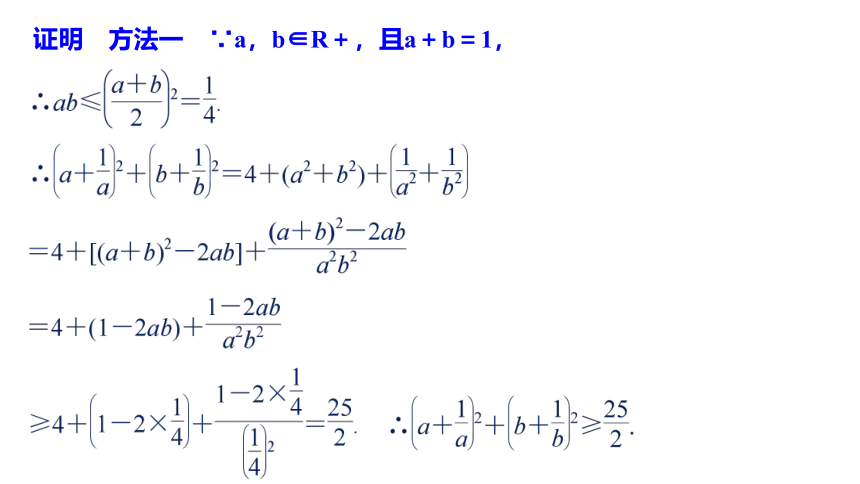
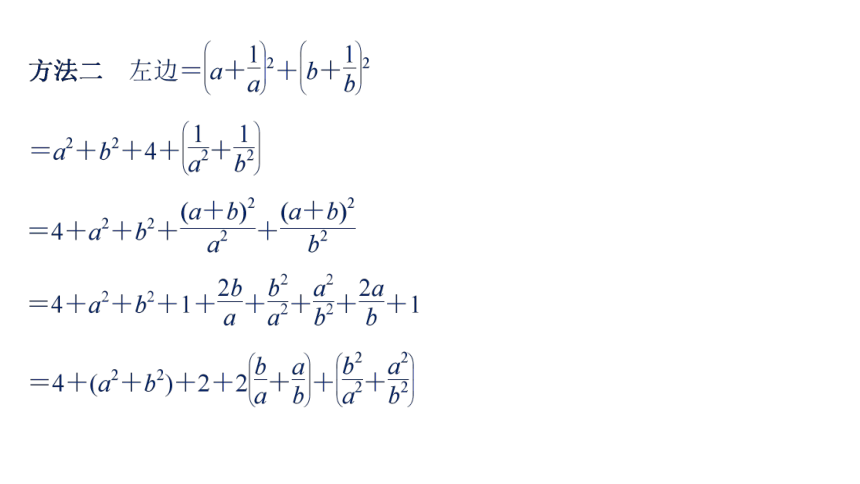
文档简介
课件31张PPT。二 综合法与分析法第二讲 证明不等式的基本方法学习目标
1.理解综合法、分析法证明不等式的原理和思维特点.
2.掌握综合法、分析法证明不等式的方法和步骤.
3.会用综合法、分析法证明一些不等式.问题导学达标检测题型探究内容索引问题导学知识点 综合法与分析法思考1 在“推理与证明”中,学习过分析法、综合法,请回顾分析法、综合法的基本特征.答案 分析法是逆推证法或执果索因法,综合法是顺推证法或由因导果法.思考2 综合法与分析法有什么区别和联系?答案 区别:综合法,由因导果,形式简洁,易于表达;
分析法,执果索因,利于思考,易于探索.
联系:都属于直接证明,常用分析法分析,用综合法表达.梳理 (1)综合法
①定义:一般地,从 出发,利用定义、公理、定理、性质等,经过一系列的 而得出命题成立,这种证明方法叫做综合法,综合法又叫顺推证法或由因导果法.
②特点:由因导果,即从“已知”看“可知”,逐步推向“未知”.
③证明的框图表示
用P表示已知条件或已有定义、定理、公理等,用Q表示所要证明的不等式,则综合法可用框图表示为已知条件推理、论证(2)分析法
①定义:证明命题时,常常从 出发,逐步寻求使它成立的
条件,直至所需条件为已知条件或一个明显成立的事实(定义、公理或已证明的定理、性质等),从而得出要证的命题成立,这种证明方法叫做分析法.这是一种“执果索因”的思考和证明方法.
②特点:执果索因,即从“未知”看“需知”,逐步靠拢“已知”.
③证明过程的框图表示
用Q表示要证明的不等式,则分析法可用框图表示为要证的结论充分题型探究类型一 综合法证明不等式证明证明 方法一 ∵a,b∈R+,且a+b=1,反思与感悟 综合法证明不等式,揭示出条件和结论之间的因果联系,为此要着力分析已知与求证之间,不等式的左右两端之间的差异与联系.合理进行转换,恰当选择已知不等式,这是证明的关键.跟踪训练1 已知x>0,y>0,且x+y=1,证明方法二 ∵x+y=1,x>0,y>0,类型二 分析法证明不等式证明又∵a,b,c是不全相等的正数,
∴(*)式等号不成立,
∴原不等式成立.跟踪训练2 已知x>0,y>0,求证:(x2+y2) >(x3+y3) .只需证(x2+y2)3>(x3+y3)2.
即证x6+3x4y2+3x2y4+y6>x6+2x3y3+y6,
即证3x4y2+3x2y4>2x3y3.
∵x>0,y>0,∴x2y2>0.即证3x2+3y2>2xy.
∵3x2+3y2>x2+y2≥2xy,
∴3x2+3y2>2xy成立.证明类型三 分析综合法证明不等式由a>0,b>0,a+b=1,∴原不等式成立.证明证明由a>0,b>0,a+b=1,
只需证a(b+m)(c+m)+b(a+m)(c+m)-c(a+m)·(b+m)>0,
即证abc+abm+acm+am2+abc+abm+bcm+bm2-abc-acm-bcm-cm2>0,
即证abc+2abm+(a+b-c)m2>0.
由于a,b,c是△ABC的边长,m>0,故有a+b>c,
即(a+b-c)m2>0.所以abc+2abm+(a+b-c)m2>0是成立的.达标检测1.若a<b<0,则下列不等式中成立的是1234解析答案√答案C1234解析3.已知x>0,y>0,证明:(1+x+y2)(1+x2+y)≥9xy.1234证明 因为x>0,y>0,证明1234即证a2+ab<2ac,即a(a+b)<2ac.
∵a,b∈R+,且a+b<2c,∴a(a+b)<2ac显然成立.
∴原不等式成立.证明1.综合法和分析法的比较
(1)相同点:都是直接证明.
(2)不同点:综合法,由因导果,形式简洁,易于表达;分析法,执果索因,利于思考,易于探索.
2.证明不等式的通常做法
常用分析法找证题切入点,用综合法写证题过程.本课结束
1.理解综合法、分析法证明不等式的原理和思维特点.
2.掌握综合法、分析法证明不等式的方法和步骤.
3.会用综合法、分析法证明一些不等式.问题导学达标检测题型探究内容索引问题导学知识点 综合法与分析法思考1 在“推理与证明”中,学习过分析法、综合法,请回顾分析法、综合法的基本特征.答案 分析法是逆推证法或执果索因法,综合法是顺推证法或由因导果法.思考2 综合法与分析法有什么区别和联系?答案 区别:综合法,由因导果,形式简洁,易于表达;
分析法,执果索因,利于思考,易于探索.
联系:都属于直接证明,常用分析法分析,用综合法表达.梳理 (1)综合法
①定义:一般地,从 出发,利用定义、公理、定理、性质等,经过一系列的 而得出命题成立,这种证明方法叫做综合法,综合法又叫顺推证法或由因导果法.
②特点:由因导果,即从“已知”看“可知”,逐步推向“未知”.
③证明的框图表示
用P表示已知条件或已有定义、定理、公理等,用Q表示所要证明的不等式,则综合法可用框图表示为已知条件推理、论证(2)分析法
①定义:证明命题时,常常从 出发,逐步寻求使它成立的
条件,直至所需条件为已知条件或一个明显成立的事实(定义、公理或已证明的定理、性质等),从而得出要证的命题成立,这种证明方法叫做分析法.这是一种“执果索因”的思考和证明方法.
②特点:执果索因,即从“未知”看“需知”,逐步靠拢“已知”.
③证明过程的框图表示
用Q表示要证明的不等式,则分析法可用框图表示为要证的结论充分题型探究类型一 综合法证明不等式证明证明 方法一 ∵a,b∈R+,且a+b=1,反思与感悟 综合法证明不等式,揭示出条件和结论之间的因果联系,为此要着力分析已知与求证之间,不等式的左右两端之间的差异与联系.合理进行转换,恰当选择已知不等式,这是证明的关键.跟踪训练1 已知x>0,y>0,且x+y=1,证明方法二 ∵x+y=1,x>0,y>0,类型二 分析法证明不等式证明又∵a,b,c是不全相等的正数,
∴(*)式等号不成立,
∴原不等式成立.跟踪训练2 已知x>0,y>0,求证:(x2+y2) >(x3+y3) .只需证(x2+y2)3>(x3+y3)2.
即证x6+3x4y2+3x2y4+y6>x6+2x3y3+y6,
即证3x4y2+3x2y4>2x3y3.
∵x>0,y>0,∴x2y2>0.即证3x2+3y2>2xy.
∵3x2+3y2>x2+y2≥2xy,
∴3x2+3y2>2xy成立.证明类型三 分析综合法证明不等式由a>0,b>0,a+b=1,∴原不等式成立.证明证明由a>0,b>0,a+b=1,
只需证a(b+m)(c+m)+b(a+m)(c+m)-c(a+m)·(b+m)>0,
即证abc+abm+acm+am2+abc+abm+bcm+bm2-abc-acm-bcm-cm2>0,
即证abc+2abm+(a+b-c)m2>0.
由于a,b,c是△ABC的边长,m>0,故有a+b>c,
即(a+b-c)m2>0.所以abc+2abm+(a+b-c)m2>0是成立的.达标检测1.若a<b<0,则下列不等式中成立的是1234解析答案√答案C1234解析3.已知x>0,y>0,证明:(1+x+y2)(1+x2+y)≥9xy.1234证明 因为x>0,y>0,证明1234即证a2+ab<2ac,即a(a+b)<2ac.
∵a,b∈R+,且a+b<2c,∴a(a+b)<2ac显然成立.
∴原不等式成立.证明1.综合法和分析法的比较
(1)相同点:都是直接证明.
(2)不同点:综合法,由因导果,形式简洁,易于表达;分析法,执果索因,利于思考,易于探索.
2.证明不等式的通常做法
常用分析法找证题切入点,用综合法写证题过程.本课结束
