第3讲 排序不等式
图片预览










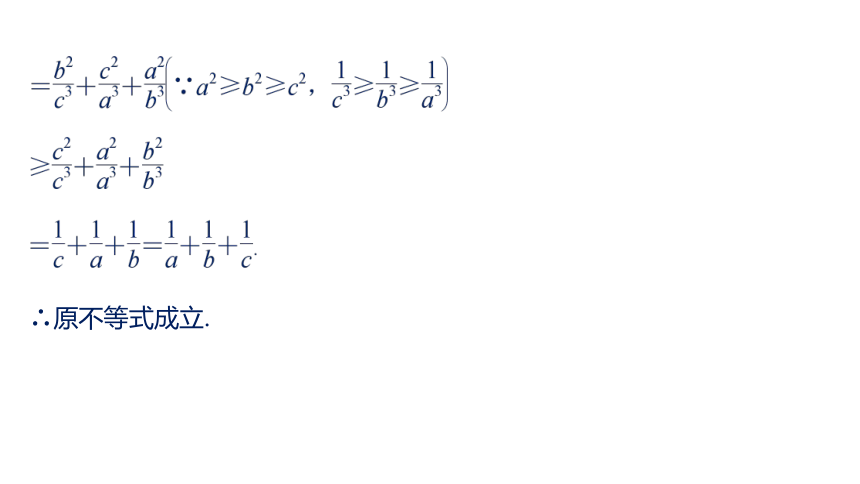
文档简介
课件35张PPT。三 排序不等式第三讲 柯西不等式与排序不等式学习目标
1.了解反序和、乱序和、顺序和等有关概念.
2.了解排序不等式及其证明的几何意义与背景.
3.掌握排序不等式的结构形式,并能简单应用.问题导学达标检测题型探究内容索引问题导学知识点 排序不等式思考1 某班学生要开联欢会,需要买价格不同的礼品4件、5件及2件,现在选择商店中单价为3元、2元和1元的礼品,问有多少种不同的购买方案?在这些方案中哪种花钱最少?哪种花钱最多?答案 (1)共有3×2×1=6(种)不同的购买方案.
(2)5×3+4×2+2×1=25(元),这种方案花钱最多;
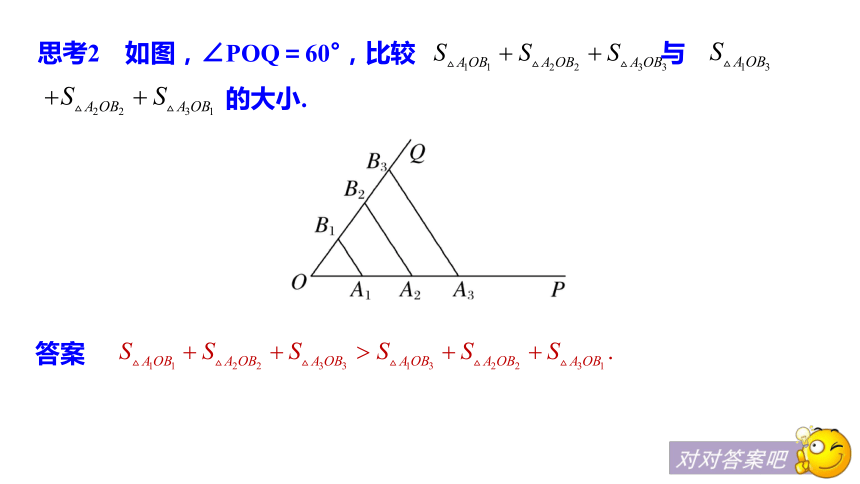
5×1+4×2+2×3=19(元),这种方案花钱最少.思考2 如图,∠POQ=60°,比较 与
的大小.答案 梳理 (1)顺序和、乱序和、反序和的概念
设有两个有序实数组:a1≤a2≤…≤an;b1≤b2≤…≤bn,c1,c2,…,cn是b1,b2,…,bn的任意一个排列.
①乱序和: .
②反序和: .
③顺序和: .S=a1c1+a2c2+…+ancnS1=a1bn+a2bn-1+…+anb1S2=a1b1+a2b2+…+anbn(2)排序不等式(排序原理)
设a1≤a2≤…≤an,b1≤b2≤…≤bn为两组实数,c1,c2,…,cn是b1,b2,…,bn的任一排列,则 ≤a1c1+a2c2+…+ancn≤ ,当且仅当a1=a2=…=an或b1=b2=…=bn时,反序和等于顺序和.a1bn+a2bn-1+…+anb1a1b1+a2b2+…+anbn题型探究类型一 利用排序不等式证明不等式命题角度1 字母已定序问题证明又顺序和不小于乱序和,故可得∴原不等式成立.反思与感悟 利用排序不等式证明不等式的技巧在于仔细观察、分析所要证明的式子的结构,从而正确地构造出不等式中所需要的带有大小顺序的两个数组.证明证明 因为0<a≤b≤c,所以0<a+b≤c+a≤b+c,又0<a2≤b2≤c2,由排序不等式可知顺序和大于等于乱序和,命题角度2 字母大小顺序不定问题证明证明 由不等式的对称性,不妨设a≥b≥c>0,由顺序和≥乱序和得到两个不等式:两式相加,得反思与感悟 对于排序不等式,其核心是必须有两组完全确定的数据,所以解题的关键是构造出这样的两组数据.跟踪训练2 设a,b,c∈R+,利用排序不等式证明:证明 不妨设0<a≤b≤c,所以由排序不等式可得证明类型二 利用排序不等式求最值解答解 由于a,b,c的对称性,不妨设a≥b≥c>0,
则a+b≥a+c≥b+c,由排序不等式,得反思与感悟 求最小(大)值,往往所给式子是顺(反)序和式.然后利用顺(反)序和不小(大)于乱序和的原理构造出一个或二个适当的乱序和,从而求出其最小(大)值.解答达标检测1.设a,b,c均为正数,且P=a3+b3+c3,Q=a2b+b2c+c2a,则P与Q的大小关系是
A.P>Q B.P≥Q C.P<Q D.P≤Q1234解析 不妨设a≥b≥c>0,
则a2≥b2≥c2>0.
由排序不等式,得a2a+b2b+c2c≥a2b+b2c+c2a,
当且仅当a=b=c时,等号成立,所以P≥Q.解析答案√2.已知a1=2,a2=7,a3=8,a4=9,a5=12,b1=3,b2=4,b3=6,b4=10,b5=11.将bi(i=1,2,3,4,5)重新排列记为c1,c2,c3,c4,c5,则a1c1+a2c2+…+a5c5的最大值是
A.324 B.314
C.304 D.212答案√1234解析 a1c1+a2c2+…+a5c5≤a1b1+a2b2+a3b3+a4b4+a5b5
=2×3+7×4+8×6+9×10+12×11=304.解析3.n个正数与这n个正数的倒数的乘积的和的最小值为____.1234n解析答案解析 设0<a1≤a2≤a3≤…≤an,则由排序不等式得,反序和≤乱序和≤顺序和.
故最小值为反序和1234证明证明 由题意不妨设a≥b>0.1.对排序不等式的理解
排序原理是对不同的两个数组来研究不同的乘积和的问题,能构造的和按数组中的某种“搭配”的顺序被分为三种形式:顺序和、反序和、乱序和,对这三种不同的搭配形式只需注意是怎样的“次序”,两种较为简单的是“顺与反”,而乱序和也就是不按“常理”的顺序了.
2.排序不等式的本质
两实数序列同方向单调(同时增或同时减)时所得两两乘积之和最大,反方向单调(一增一减)时所得两两乘积之和最小.3.排序不等式取等号的条件
等号成立的条件是其中一序列为常数序列,即a1=a2=…=an或b1=b2=b3=…=bn.
4.排序原理的思想
在解答数学问题时,常常涉及一些可以比较大小的量,它们之间并没有预先规定大小顺序,那么在解答问题时,我们可以利用排序原理的思想方法,将它们按一定顺序排列起来,继而利用不等关系来解题.因此,对于排序原理,我们记住的是处理问题的这种思想及方法,同时要学会善于利用这种比较经典的结论来处理实际问题.本课结束
1.了解反序和、乱序和、顺序和等有关概念.
2.了解排序不等式及其证明的几何意义与背景.
3.掌握排序不等式的结构形式,并能简单应用.问题导学达标检测题型探究内容索引问题导学知识点 排序不等式思考1 某班学生要开联欢会,需要买价格不同的礼品4件、5件及2件,现在选择商店中单价为3元、2元和1元的礼品,问有多少种不同的购买方案?在这些方案中哪种花钱最少?哪种花钱最多?答案 (1)共有3×2×1=6(种)不同的购买方案.
(2)5×3+4×2+2×1=25(元),这种方案花钱最多;
5×1+4×2+2×3=19(元),这种方案花钱最少.思考2 如图,∠POQ=60°,比较 与
的大小.答案 梳理 (1)顺序和、乱序和、反序和的概念
设有两个有序实数组:a1≤a2≤…≤an;b1≤b2≤…≤bn,c1,c2,…,cn是b1,b2,…,bn的任意一个排列.
①乱序和: .
②反序和: .
③顺序和: .S=a1c1+a2c2+…+ancnS1=a1bn+a2bn-1+…+anb1S2=a1b1+a2b2+…+anbn(2)排序不等式(排序原理)
设a1≤a2≤…≤an,b1≤b2≤…≤bn为两组实数,c1,c2,…,cn是b1,b2,…,bn的任一排列,则 ≤a1c1+a2c2+…+ancn≤ ,当且仅当a1=a2=…=an或b1=b2=…=bn时,反序和等于顺序和.a1bn+a2bn-1+…+anb1a1b1+a2b2+…+anbn题型探究类型一 利用排序不等式证明不等式命题角度1 字母已定序问题证明又顺序和不小于乱序和,故可得∴原不等式成立.反思与感悟 利用排序不等式证明不等式的技巧在于仔细观察、分析所要证明的式子的结构,从而正确地构造出不等式中所需要的带有大小顺序的两个数组.证明证明 因为0<a≤b≤c,所以0<a+b≤c+a≤b+c,又0<a2≤b2≤c2,由排序不等式可知顺序和大于等于乱序和,命题角度2 字母大小顺序不定问题证明证明 由不等式的对称性,不妨设a≥b≥c>0,由顺序和≥乱序和得到两个不等式:两式相加,得反思与感悟 对于排序不等式,其核心是必须有两组完全确定的数据,所以解题的关键是构造出这样的两组数据.跟踪训练2 设a,b,c∈R+,利用排序不等式证明:证明 不妨设0<a≤b≤c,所以由排序不等式可得证明类型二 利用排序不等式求最值解答解 由于a,b,c的对称性,不妨设a≥b≥c>0,
则a+b≥a+c≥b+c,由排序不等式,得反思与感悟 求最小(大)值,往往所给式子是顺(反)序和式.然后利用顺(反)序和不小(大)于乱序和的原理构造出一个或二个适当的乱序和,从而求出其最小(大)值.解答达标检测1.设a,b,c均为正数,且P=a3+b3+c3,Q=a2b+b2c+c2a,则P与Q的大小关系是
A.P>Q B.P≥Q C.P<Q D.P≤Q1234解析 不妨设a≥b≥c>0,
则a2≥b2≥c2>0.
由排序不等式,得a2a+b2b+c2c≥a2b+b2c+c2a,
当且仅当a=b=c时,等号成立,所以P≥Q.解析答案√2.已知a1=2,a2=7,a3=8,a4=9,a5=12,b1=3,b2=4,b3=6,b4=10,b5=11.将bi(i=1,2,3,4,5)重新排列记为c1,c2,c3,c4,c5,则a1c1+a2c2+…+a5c5的最大值是
A.324 B.314
C.304 D.212答案√1234解析 a1c1+a2c2+…+a5c5≤a1b1+a2b2+a3b3+a4b4+a5b5
=2×3+7×4+8×6+9×10+12×11=304.解析3.n个正数与这n个正数的倒数的乘积的和的最小值为____.1234n解析答案解析 设0<a1≤a2≤a3≤…≤an,则由排序不等式得,反序和≤乱序和≤顺序和.
故最小值为反序和1234证明证明 由题意不妨设a≥b>0.1.对排序不等式的理解
排序原理是对不同的两个数组来研究不同的乘积和的问题,能构造的和按数组中的某种“搭配”的顺序被分为三种形式:顺序和、反序和、乱序和,对这三种不同的搭配形式只需注意是怎样的“次序”,两种较为简单的是“顺与反”,而乱序和也就是不按“常理”的顺序了.
2.排序不等式的本质
两实数序列同方向单调(同时增或同时减)时所得两两乘积之和最大,反方向单调(一增一减)时所得两两乘积之和最小.3.排序不等式取等号的条件
等号成立的条件是其中一序列为常数序列,即a1=a2=…=an或b1=b2=b3=…=bn.
4.排序原理的思想
在解答数学问题时,常常涉及一些可以比较大小的量,它们之间并没有预先规定大小顺序,那么在解答问题时,我们可以利用排序原理的思想方法,将它们按一定顺序排列起来,继而利用不等关系来解题.因此,对于排序原理,我们记住的是处理问题的这种思想及方法,同时要学会善于利用这种比较经典的结论来处理实际问题.本课结束
