第3讲 柯西不等式与排序不等式复习课
文档属性
| 名称 | 第3讲 柯西不等式与排序不等式复习课 |

|
|
| 格式 | zip | ||
| 文件大小 | 4.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-05 16:19:56 | ||
图片预览











文档简介
课件33张PPT。复习课第三讲 柯西不等式与排序不等式学习目标
1.梳理本专题主要知识,构建知识网络.
2.进一步理解柯西不等式,熟练掌握柯西不等式的各种形式及应用技巧.
3.理解排序不等式及应用.
4.进一步体会柯西不等式与排序不等式所蕴含的数学思想及方法.知识梳理达标检测题型探究内容索引知识梳理1.二维形式的柯西不等式
(1)二维形式的柯西不等式:_______________________________________
_________.
(2)柯西不等式的向量形式:_______________________________________
______________________________________________.
(3)二维形式的三角不等式:设x1,y1,x2,y2∈R,那么
______________________________________.若a,b,c,d都是实数,则(a2+b2)(c2+d2)≥(ac+bd)2 设α,β是两个向量,则|α·β|≤|α||β|,当且仅当β是零向量,或存在实数k,使α=kβ时,等号成立2.一般形式的柯西不等式
设a1,a2,a3,…,an,b1,b2,b3,…,bn是实数,则_______________
_______________________________________.当且仅当bi=0(i=1,2,…,n)或存在一个数k,使得ai=kbi(i=1,2,…,n)时,等号成立.
3.排序不等式
设a1≤a2≤…≤an,b1≤b2≤…≤bn为两组实数,c1,c2,…,cn是b1,b2,…,bn的任一排列,则a1bn+a2bn-1+…+anb1≤__________________
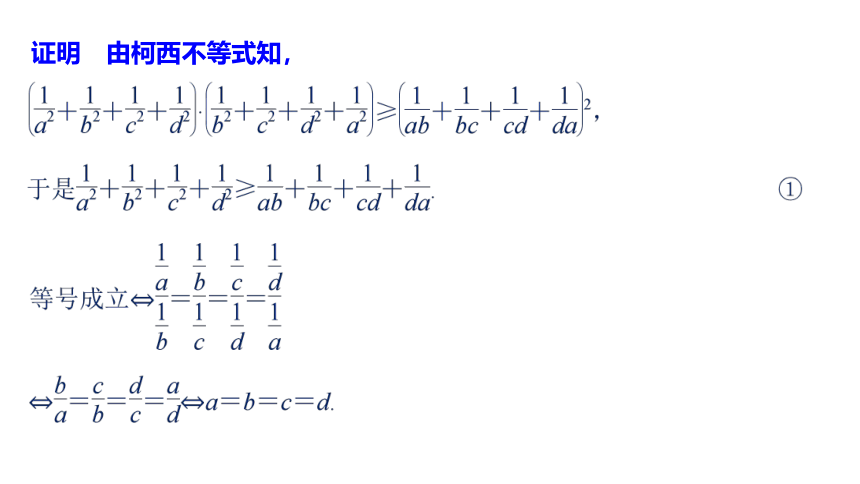
≤a1b1+a2b2+…+anbn.a1c1+a2c2+…+ancn题型探究类型一 利用柯西不等式证明不等式证明证明 由柯西不等式知,又已知a,b,c,d不全相等,则①中等号不成立.反思与感悟 利用柯西不等式证题的技巧(2)利用柯西不等式证明其他不等式的关键是构造两组数,并向着柯西不等式的形式进行转化,运用时要注意体会.证明类型二 利用排序不等式证明不等式证明 不妨设0<a≤b≤c,于是A≤B≤C.
由排序不等式,得
aA+bB+cC=aA+bB+cC,
aA+bB+cC≥bA+cB+aC,
aA+bB+cC≥cA+aB+bC.
相加,得3(aA+bB+cC)≥(a+b+c)·(A+B+C)证明引申探究证明 不妨设0<a≤b≤c,于是A≤B≤C.
由0<b+c-a,0<a+b-c,0<a+c-b,
有0<A(b+c-a)+C(a+b-c)+B(a+c-b)
=a(B+C-A)+b(A+C-B)+c(A+B-C)
=a(π-2A)+b(π-2B)+c(π-2C)
=(a+b+c)π-2(aA+bB+cC).证明反思与感悟 利用排序不等式证明不等式的策略
(1)在利用排序不等式证明不等式时,首先考虑构造出两个合适的有序数组,并能根据需要进行恰当地组合.这需要结合题目的已知条件及待证不等式的结构特点进行合理选择.
(2)根据排序不等式的特点,与多变量间的大小顺序有关的不等式问题,利用排序不等式解决往往很简捷.证明证明 由a,b,c的对称性,不妨设a≥b≥c,由排序不等式,得再次由排序不等式,得类型三 利用柯西不等式或排序不等式求最值例3 (1)求实数x,y的值使得(y-1)2+(x+y-3)2+(2x+y-6)2达到最小值.解 由柯西不等式,得
(12+22+12)×[(y-1)2+(3-x-y)2+(2x+y-6)2]
≥[1×(y-1)+2×(3-x-y)+1×(2x+y-6)]2=1,解答解答解 设b1,b2,b3,b4,b5是a1,a2,a3,a4,a5的一个排列,
且b1<b2<b3<b4<b5.
因此b1≥1,b2≥2,b3≥3,b4≥4,b5≥5.由排序不等式,得反思与感悟 利用柯西或排序不等式求最值的技巧
(1)有关不等式问题往往要涉及对式子或量的范围的限定,其中含有多变量限制条件的最值问题往往难以处理.在这类题目中,利用柯西不等式或排序不等式处理往往比较容易.
(2)在利用柯西不等式或排序不等式求最值时,要关注等号成立的条件,不能忽略.解答达标检测1234解析答案√=3×3=9.
∴y≤3,y的最大值为3.2.已知实数a,b,c,d满足a+b+c+d=3,a2+2b2+3c2+6d2=5,则a的最大值是
A.1 B.2 C.3 D.4解析答案√1234即2b2+3c2+6d2≥(b+c+d)2.
∴5-a2≥(3-a)2.
解得1≤a≤2.
验证:当a=2时,等号成立.3.已知2x+3y+4z=10,则x2+y2+z2取到最小值时的x,y,z的值为√解析 由柯西不等式得
(22+32+42)(x2+y2+z2)≥(2x+3y+4z)2,1234解析答案1234证明证明 不妨设a≥b≥c>0,1.对于柯西不等式要特别注意其向量形式的几何意义,从柯西不等式的几何意义出发就得到了三角形式的柯西不等式,柯西不等式的一般形式也可以写成向量形式.
2.参数配方法是由旧知识得到的新方法,注意体会此方法的数学思想.
3.对于排序不等式要抓住它的本质含义:两实数序列同方向单调(同时增或同时减)时所得两两乘积之和最大,反方向单调(一增一减)时所得两两乘积之和最小,注意等号成立条件是其中一序列为常数序列.4.数学建模是数学学习中的一种新形式,它为学生提供了自己学习的空间,有助于学生了解数学在实际生活中的应用,体会数学与日常生活及其他学科的联系.本课结束
1.梳理本专题主要知识,构建知识网络.
2.进一步理解柯西不等式,熟练掌握柯西不等式的各种形式及应用技巧.
3.理解排序不等式及应用.
4.进一步体会柯西不等式与排序不等式所蕴含的数学思想及方法.知识梳理达标检测题型探究内容索引知识梳理1.二维形式的柯西不等式
(1)二维形式的柯西不等式:_______________________________________
_________.
(2)柯西不等式的向量形式:_______________________________________
______________________________________________.
(3)二维形式的三角不等式:设x1,y1,x2,y2∈R,那么
______________________________________.若a,b,c,d都是实数,则(a2+b2)(c2+d2)≥(ac+bd)2 设α,β是两个向量,则|α·β|≤|α||β|,当且仅当β是零向量,或存在实数k,使α=kβ时,等号成立2.一般形式的柯西不等式
设a1,a2,a3,…,an,b1,b2,b3,…,bn是实数,则_______________
_______________________________________.当且仅当bi=0(i=1,2,…,n)或存在一个数k,使得ai=kbi(i=1,2,…,n)时,等号成立.
3.排序不等式
设a1≤a2≤…≤an,b1≤b2≤…≤bn为两组实数,c1,c2,…,cn是b1,b2,…,bn的任一排列,则a1bn+a2bn-1+…+anb1≤__________________
≤a1b1+a2b2+…+anbn.a1c1+a2c2+…+ancn题型探究类型一 利用柯西不等式证明不等式证明证明 由柯西不等式知,又已知a,b,c,d不全相等,则①中等号不成立.反思与感悟 利用柯西不等式证题的技巧(2)利用柯西不等式证明其他不等式的关键是构造两组数,并向着柯西不等式的形式进行转化,运用时要注意体会.证明类型二 利用排序不等式证明不等式证明 不妨设0<a≤b≤c,于是A≤B≤C.
由排序不等式,得
aA+bB+cC=aA+bB+cC,
aA+bB+cC≥bA+cB+aC,
aA+bB+cC≥cA+aB+bC.
相加,得3(aA+bB+cC)≥(a+b+c)·(A+B+C)证明引申探究证明 不妨设0<a≤b≤c,于是A≤B≤C.
由0<b+c-a,0<a+b-c,0<a+c-b,
有0<A(b+c-a)+C(a+b-c)+B(a+c-b)
=a(B+C-A)+b(A+C-B)+c(A+B-C)
=a(π-2A)+b(π-2B)+c(π-2C)
=(a+b+c)π-2(aA+bB+cC).证明反思与感悟 利用排序不等式证明不等式的策略
(1)在利用排序不等式证明不等式时,首先考虑构造出两个合适的有序数组,并能根据需要进行恰当地组合.这需要结合题目的已知条件及待证不等式的结构特点进行合理选择.
(2)根据排序不等式的特点,与多变量间的大小顺序有关的不等式问题,利用排序不等式解决往往很简捷.证明证明 由a,b,c的对称性,不妨设a≥b≥c,由排序不等式,得再次由排序不等式,得类型三 利用柯西不等式或排序不等式求最值例3 (1)求实数x,y的值使得(y-1)2+(x+y-3)2+(2x+y-6)2达到最小值.解 由柯西不等式,得
(12+22+12)×[(y-1)2+(3-x-y)2+(2x+y-6)2]
≥[1×(y-1)+2×(3-x-y)+1×(2x+y-6)]2=1,解答解答解 设b1,b2,b3,b4,b5是a1,a2,a3,a4,a5的一个排列,
且b1<b2<b3<b4<b5.
因此b1≥1,b2≥2,b3≥3,b4≥4,b5≥5.由排序不等式,得反思与感悟 利用柯西或排序不等式求最值的技巧
(1)有关不等式问题往往要涉及对式子或量的范围的限定,其中含有多变量限制条件的最值问题往往难以处理.在这类题目中,利用柯西不等式或排序不等式处理往往比较容易.
(2)在利用柯西不等式或排序不等式求最值时,要关注等号成立的条件,不能忽略.解答达标检测1234解析答案√=3×3=9.
∴y≤3,y的最大值为3.2.已知实数a,b,c,d满足a+b+c+d=3,a2+2b2+3c2+6d2=5,则a的最大值是
A.1 B.2 C.3 D.4解析答案√1234即2b2+3c2+6d2≥(b+c+d)2.
∴5-a2≥(3-a)2.
解得1≤a≤2.
验证:当a=2时,等号成立.3.已知2x+3y+4z=10,则x2+y2+z2取到最小值时的x,y,z的值为√解析 由柯西不等式得
(22+32+42)(x2+y2+z2)≥(2x+3y+4z)2,1234解析答案1234证明证明 不妨设a≥b≥c>0,1.对于柯西不等式要特别注意其向量形式的几何意义,从柯西不等式的几何意义出发就得到了三角形式的柯西不等式,柯西不等式的一般形式也可以写成向量形式.
2.参数配方法是由旧知识得到的新方法,注意体会此方法的数学思想.
3.对于排序不等式要抓住它的本质含义:两实数序列同方向单调(同时增或同时减)时所得两两乘积之和最大,反方向单调(一增一减)时所得两两乘积之和最小,注意等号成立条件是其中一序列为常数序列.4.数学建模是数学学习中的一种新形式,它为学生提供了自己学习的空间,有助于学生了解数学在实际生活中的应用,体会数学与日常生活及其他学科的联系.本课结束
